Thấy rõ hơn bản chất "tích lũy – bứt phá – phi tuyến" trong đời sống

🔍 1. Lỗi tư duy phổ biến: "Kỳ vọng tuyến tính"

• Nội dung: Nhiều người tưởng rằng nỗ lực hôm nay sẽ mang lại kết quả ngay ngày mai, theo kiểu mỗi ngày +1 đơn hàng sẽ dẫn đến 10 đơn sau 10 ngày.
• Bài học: → Đời sống và công việc không vận hành tuyến tính. Có những thành quả đòi hỏi độ trễ tự nhiên — giống như gieo hạt cần thời gian nảy mầm. → Thay vì thất vọng khi không thấy kết quả sớm, hãy hiểu rằng mình đang đi qua giai đoạn "vô hình" của thành công.

🌀 2. Hiểu đúng về sự tích lũy và lộ trình tăng trưởng

• Nội dung: Thay đổi thực sự đến từ sự tích tụ — không phải “bật công tắc”.
• Bài học: → Thành công bền vững là kết quả của những hành động lặp đi lặp lại, nhỏ nhưng đều đặn. → Cần kiên nhẫn và tin tưởng vào tiến trình, kể cả khi chưa thấy tín hiệu gì.

🧠 3. Cái bẫy của kỳ vọng sớm và nỗi nghi ngờ bản thân

• Nội dung: Những điều vĩ đại thường trông "ngớ ngẩn" lúc đầu. Cả người khác lẫn chính mình đều dễ nghi ngờ.
• Bài học: → Mọi thứ đáng giá đều bắt đầu từ sự mơ hồ và thiếu rõ ràng. → Giai đoạn không có gì xảy ra là bình thường, không phải dấu hiệu của thất bại. Đó chỉ là giai đoạn mà nhiều người bỏ cuộc nhất.

📈 4. Đường cong lũy tiến và sự “bứt phá”

• Nội dung: Kết quả không đến theo đường thẳng, mà theo một đường cong có độ trễ.
• Bài học: → Bạn có thể đang ở đoạn đầu phẳng lặng của đường cong. Tiếp tục mới là cách duy nhất để bước sang giai đoạn “bật lên”. → Không cần “đốt cháy giai đoạn” — bứt phá sẽ đến tự nhiên nếu bạn kiên trì.

🧗 5. Lộ trình khả thi là lộ trình có “độ dốc vừa phải”

• Nội dung: Hãy chia nhỏ mục tiêu, bắt đầu từ việc nhỏ nhất có thể.
• Bài học: → Thay vì bị choáng ngợp bởi cái đích, hãy tập trung vào một hành động nhỏ ngay hôm nay. → Sức mạnh nằm ở nhịp điệu chứ không phải ở “cao trào”. Thói quen, sự đều đặn là yếu tố tạo ra sự đột phá về sau.

🌄 6. Niềm tin vào hành trình

• Nội dung: Không thấy đích không có nghĩa là không có đích. Có thể bạn đang ở khúc quanh của một cầu thang xoắn.
• Bài học: → Tiếp tục bước là cách duy nhất để đi đến tận cùng — chỉ cần bạn không dừng lại. → Có những mục tiêu không đòi hỏi tài năng xuất chúng, mà chỉ cần sự bền bỉ không đứt gãy.

✨ Triết lý cốt lõi:

"Đừng nghĩ về mục tiêu như một điểm đến xa xôi, mà hãy nghĩ về nó như một nhịp điệu sống."

🔢 Mô phỏng bằng Toán học & Machine Learning

📈 1. Đường cong phi tuyến – Quy luật lũy tiến

✅ Toán học:

• Ta có một hàm tăng trưởng theo thời gian:

  $$y(t) = a \cdot (1 - e^{-bt})$$

  Đây là một hàm tiệm cận dạng sigmoid, phản ánh:

  • Lúc đầu: tăng rất chậm (giai đoạn nghi ngờ, bế tắc).
  • Sau đó: tăng mạnh khi vượt ngưỡng tích lũy.
  • Cuối cùng: tiệm cận, khi đã đạt đỉnh năng lực hoặc giới hạn mô hình.

✅ ML analogy: Learning curve

• Khi huấn luyện mô hình học máy (ML), bạn sẽ thấy learning curve lúc đầu gần như phẳng:

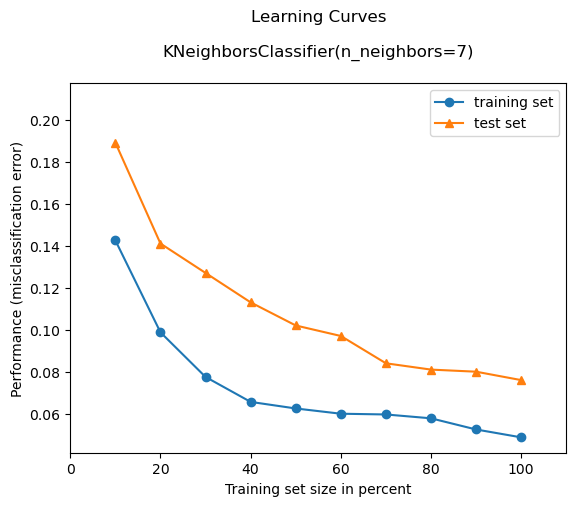
  (Ví dụ learning curve trong ML: mất nhiều epoch đầu chưa cải thiện rõ accuracy)

  • Nhưng nếu kiên trì, mô hình dần học được các pattern, accuracy cải thiện theo kiểu phi tuyến.
  • Nếu dừng sớm vì "không thấy tiến triển" → bạn bỏ lỡ đoạn bật mạnh về sau.

⏳ 2. Độ trễ – Time Lag

✅ Toán học:

• Một hiện tượng có delay thường được mô tả bằng differential equation có trễ:

  $$\frac{dy(t)}{dt} = f(y(t - \tau))$$

  → Kết quả hôm nay không phải do việc hôm nay làm, mà từ việc đã làm từ trước. → Giống như bạn chạy ads, hôm nay không có đơn, nhưng đơn sẽ đến sau 1–2 tuần (tương tự delayed feedback loop trong Reinforcement Learning).

✅ ML analogy:

• Reinforcement Learning (Học tăng cường):

  • Agent (người hành động) chọn hành động ngay bây giờ, nhưng phần thưởng có thể đến muộn.

  • Vì thế, cần dùng discount factor γ < 1 để ghi nhận giá trị của các kết quả đến sau.

  • Ví dụ trong Q-learning:

    $$Q(s, a) \leftarrow Q(s, a) + \alpha \left[ r + \gamma \cdot \max Q(s', a') - Q(s, a) \right]$$

  • → Nếu bạn nghĩ kết quả sẽ đến ngay lập tức, bạn không học được gì cả.

⚙️ 3. Gradient Descent – Tích lũy tiệm tiến

✅ Toán học:

• Gradient Descent cập nhật theo:

  $$\theta_{t+1} = \theta_t - \eta \cdot \nabla J(\theta_t)$$

  → Chỉ một bước nhỏ mỗi lần, nhưng lặp lại đủ nhiều sẽ dẫn đến tối ưu. → Nếu bạn dừng lại ở iteration thứ 10 vì chưa thấy gì, bạn không bao giờ đến được điểm tối ưu.

✅ Bài học sống còn:

• Thành công cũng như quá trình học mô hình tốt:

  • Cần kiên nhẫn tích lũy từng bước nhỏ (learning rate).
  • Không có bước nào “đột phá” ngay — tất cả đều là tích góp vi mô dẫn đến thay đổi vĩ mô.

🔁 4. Overfitting vs. Generalization – Đừng kỳ vọng sớm

✅ ML analogy:

• Nếu bạn quá tập trung vào “kết quả sớm” (train accuracy tăng rất nhanh), rất dễ:

  • Overfit: học tủ, ảo tưởng kết quả.
  • Không generalize: ra thực tế lại kém.

• Còn nếu bạn huấn luyện chậm rãi, theo early stopping + regularization, bạn đạt mô hình bền vững hơn.

→ Tương tự, người tìm “kết quả sớm” trong đời sống dễ chọn shortcut (chạy ads bừa, học tủ, bỏ tiền kiếm lời ngay) → nhưng dễ thất vọng.

✅ Tổng kết bằng một mô hình toán học cho đời sống:

Giả sử bạn đang tích lũy giá trị theo thời gian $t$, với "độ trễ" và "tăng trưởng lũy tiến", mô hình thành công cá nhân có thể mô phỏng bằng:

$$\text{Success}(t) = \int_{0}^{t} e^{-\lambda(t - \tau)} \cdot f(\tau) \, d\tau$$

• $f(\tau)$: Nỗ lực bạn bỏ ra tại thời điểm $\tau$
• $e^{-\lambda(t - \tau)}$: Yếu tố độ trễ (effort hôm nay sẽ tạo ra kết quả sau một khoảng thời gian)
• → Tổng nỗ lực được “cộng dồn có trễ” sẽ dẫn đến thành công.