Sinh dữ liệu với mô hình dựa trên score

Bài đăng này đã không được cập nhật trong 2 năm

Chúng ta đã tìm hiểu về cách huấn luyện mô hình score và cách lấy mẫu với Langevin dynamics. Tuy nhiên cách làm trực tiếp đó chưa đủ để sinh ra dữ liệu tốt. Trong bài này chúng ta sẽ tìm hiểu về cách để xây dựng một mô hình score mạnh.

Ước lượng score của biến ngẫu nhiên ẩn

Thay vì ước lượng trực tiếp score của dữ liệu ban đầu, ta có thể áp dụng score matching cho biến ẩn của mô hình sinh. Ví dụ với mô hình variational autoencoder, ta sẽ cực đại ELBO thay vì $\log$ likelihood

$\mathbb{E}_{q_{\phi}(.|x)}[\log p(x, z) - \log q_{\phi}(z|x)]$

Việc tính ELBO gặp vấn đề ở entropy $H(q)=\mathbb{E}_{q_{\phi}(.|x)}[ \log q_{\phi}(z|x)]$ do ta cần biết chính xác hàm mật độ. Cách làm quen thuộc là xấp xỉ $q(z)$ bởi một phân bố chuẩn, với hàm mật độ có công thức cho trước. Một cách giải quyết khác là biến đổi entropy theo score của $q$ , cách làm này giúp $q(z)$ đa dạng hơn thay vì chỉ là phân bố chuẩn như trong VAE.

Ta sẽ áp dụng reparameterization trick, đặt $z=g_x(\epsilon),\, \epsilon\sim p(\epsilon)$ , hàm $g_x(\epsilon)$ sẽ đóng vai trò như encoder, nhận dữ liệu $x$ và nhiễu $\epsilon$ và sinh ra $z$

$\begin{aligned} -\nabla_{\phi}H(q_{\phi})&=\mathbb{E}_{q_{\phi}(.|x)}[\log q_{\phi}(z|x)]\\ &= \nabla_{\phi}\int \log q(z|x) dQ(z|x)\\ &=\nabla_{\phi}\int\log q(z|x) dg_{x*}P(z)\\ &= \nabla_{\phi}\int\log q(g_x(\epsilon)|x)dP(\epsilon)\quad &\text{đổi biến}\\ &=\int\nabla_{\phi}\log q(g_x(\epsilon)|x)dP(\epsilon)\quad &\text{tính tuyến tính của }\nabla\\ &=\int\nabla_{z}\log q(z|x) \nabla_{\phi}g_x(\epsilon) dP(\epsilon)\quad &\text{chain rule} \end{aligned}$

Như vậy gradient của entropy có thể tính được thông qua score của $q$ , mô hình bởi một hàm $s(z,x)$ , và Jacobian $\nabla_{\phi}z= \nabla_{\phi}g_x(\epsilon)$ của $z$ . Để việc cài đặt thuận tiện hơn, ta sẽ không tính trực tiếp gradient của entropy mà sẽ tính trước $s(z,x)$ mà không có gradient, sau đó tối ưu $s(z,x)^{\intercal}z$ , gradient của đại lượng này chính là gradient của entropy, và lúc này có thể kết hợp với các bộ tối ưu có sẵn.

Đại lượng còn lại có thể tách thành $\mathbb{E}_{q_{\phi}(.|x)}[\log p(x|z) - \log p(z)]$ như thông thường, với giả sử prior $p(z)$ tuân theo phân bố chuẩn.

Tổng hợp lại, mô hình VAE huấn luyện với score sẽ gồm một autoencoder như trong VAE thông thường, và ELBO được ước lượng bởi một hàm score xấp xỉ score của $q(z|x)$ , huấn luyện bởi score matching.

Các bạn có thể tham khảo code của tác giả tại đây

Sinh dữ liệu với mô hình score

Như đã nói ở phần mở đầu, phương pháp score matching cơ bản cùng với Langevin dynamics không đủ để sinh ra dữ liệu đủ tốt. Trước hết hãy xem ví dụ sau: Sử dụng Langevin dynamics để lấy mẫu từ phân bố tổng hợp của 2 phân bố chuẩn $p_1=\mathcal{N}([5, 5]^{\intercal}, I)$ và $p_2=\mathcal{N}([-5, -5]^{\intercal}, I)$ với trọng số là $[0.8, 0.2]$ như hình bên dưới

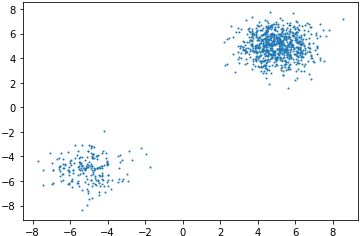
Ta có thể thấy phân bố này có 2 mode với xác suất cao nhưng cách xa nhau. Thuật toán SGLD do đó sẽ khó có thể di chuyển giữa 2 mode này. Lấy mẫu $1000$ điểm với Langevin dynamics 100 bước, step size $0.01$ , ta được như hình dưới

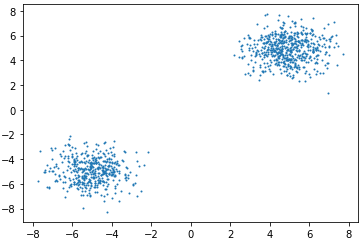
Code minh họa có thể xem ở đây

Điều này có thể giải thích như sau: Với phân bố tổng hợp $p=\alpha p_1 +(1-\alpha)p_2$ , tại những điểm có tỉ lệ xác suất của hai phân bố lớn thì score gần như không ảnh hưởng bởi trọng số. Giả sử xác suất tại $x$ theo $p_2$ gần bằng $0$ , $p(x)\approx \alpha p_1(x)$ , score tại $x$ sẽ là

$\nabla_x\log p(x) \approx \nabla_x\log\alpha p_1(x) =\nabla_x\log p_1(x)$

Ngoài ra, còn một vấn đề nữa nằm ở phương pháp score matching. Nhắc lại, mục tiêu của score matching là cực tiểu khoảng cách $l_2$ giữa hàm score mô phỏng và score thực tế của phân bố

$F(p, q) = \int_{\mathbb{R}^d} ||\nabla \log q(x)-\nabla\log p(x)||^2p(x)dx$

Tuy nhiên nhưng điểm có xác suất $p(x)$ thấp rất khó xuất hiện trong tập dữ liệu, do đó hàm mục tiêu sẽ không thể tối ưu tại các điểm này. Một ví dụ với bộ MNIST sử dụng denoise score matching, hàm score là mạng ResNet cho kết quả sau 200 epochs như sau

Để giải quyết điều này, ta có thể thêm nhiễu vào dữ liệu ban đầu. Lúc này, phân bố của nhiễu sẽ giúp tăng xác suất tại các vùng có mật độ xác suất thấp, giúp Langevin dynamics có thể hoạt động đúng.

Một vấn đề đặt ra là thêm nhiễu như thế nào mới phù hợp. Chú ý rằng denoise score matching cũng hoạt động bằng cách thêm nhiễu vào dữ liệu, tuy nhiên vẫn chưa thể học phân bố của bộ MNIST. Giả sử nhiễu có phân bố chuẩn, nếu phương sai của nhiễu lớn thì dữ liệu sẽ bị sai lệch đi nhiều, ngược lại nếu phương sai nhỏ, các vùng có xác suất thấp vẫn chưa thể tăng lên đáng kể để Langevin dynamics hoạt động (denoise score matching rơi vào trường hợp 2).

Thay vì chỉ thêm một loại nhiễu, ta có thể dùng một chuỗi gồm $L$ nhiễu với phương sai $\{\sigma_i\}^L_{i=1}$ , lần lượt thêm từng nhiễu vào trong quá trình lấy mẫu. Ở các bước đầu, ta muốn nhiễu có độ phủ lớn để SGLD dễ dàng di chuyển giữa các mode, sau đó phương sai giảm dần để phân bố gần với phân bố gốc của dữ liệu. Do đó, phương sai sẽ có tính chất $\sigma_i >\sigma_j$ với $i<j$ . Chuỗi $\{\sigma_i\}^L_{i=1}$ sẽ được chọn là chuỗi hình học $\{a\gamma^i\}^L$ , với $\sigma_1=a\gamma$ đủ lớn để phủ các vùng mật độ thấp và $\sigma_L=a\gamma^L$ đủ nhỏ để tránh sai lệch với phân bố gốc.

Hàm score lúc này cũng sẽ phụ thuộc vào phương sai để nhận biết SGLD đang ở bước nào. Thay vì dùng 1 hàm score $s(x)$ , ta sẽ dùng $L$ hàm score $s(x, \sigma_i)$ .

Mục tiêu lúc này trở thành cực tiểu Fisher divergence trên tất cả các mức độ nhiễu, với $\sigma_i$ ta sẽ cực tiểu

$F(p_{\sigma_i}, q_{\sigma_i}) = \int_{\mathbb{R}^d} ||\nabla s(x, \sigma_i)-\nabla\log p_{\sigma_i}(x)||^2p_{\sigma_i}(x)dx$

Cách đơn giản nhất để làm điều này là đặt $s(x, \sigma_i)=\frac{s(x)}{\sigma_i}$ , điều này đến từ quan sát sau: Cực tiểu $F(p_{\sigma_i}, q_{\sigma_i})$ tương đương với cực tiểu khoảng cách $l_2$ giữa $s_{\sigma_i}(\tilde x)$ và score $\frac{1}{\sigma_i^2}(x-\tilde x)$ của $\mathcal{N}(\tilde x|x, \sigma_i^2I)$ như phân tích ở bài trước, và $x-\tilde x \sim \mathcal{N}(0, \sigma_i^2I)$ .

Mô hình này được gọi là Noise conditional score network (NSCN). Hàm mục tiêu sẽ là tổng của loss trên tất cả mức độ nhiễu, với trọng số là $\sigma_i^2$

$L = \sum_{i=1}^L\sigma_i^2F(p_{\sigma_i}, q_{\sigma_i})$

Ta cũng cần một thuật toán lấy mẫu mới phù hợp với cách mô hình này. Thay vì dùng Langevin dynamics với một phân bố duy nhất, ta chia quá trình lấy mẫu thành $L$ bước lần lượt, bước thứ $i$ sẽ bắt đầu Langevin dynamics ở bước $i-1$ và lấy mẫu với phân bố mục tiêu là $q_{\sigma_i}$ . Phân bố $q_{\sigma_i}$ sẽ có nhiễu lớn hơn $q_{\sigma_j}$ với $i<j$ , do đó step size cũng sẽ lớn hơn. Tỉ lệ step size thường dùng là $\frac{\sigma_i^2}{\sigma_L^2}$ tại bước $i$ . Đây là thuật toán annealed Langevin dynamics.

Thử huấn luyện mô hình NCSN với score là mạng ResNet giống như trên cho ra kết quả chấp nhận được sau 200 epochs

Các bạn có thể tham khảo code của tác giả tại đây hoặc code mình cài đặt lại cho bài này tại đây

Kết

Bài này đã giới thiệu về các cách cải tiến và áp dụng mô hình sinh dựa trên score. Trong bài tiếp theo, chúng ta sẽ tìm hiểu về mô hình tổng quát hơn của score based model.