I. Mở đầu

Trong những bài viết trước, các bạn đã được giới thiệu tuần tự những chiến lược giải thuật từ đơn giản tới nâng cao, như đệ quy, quay lui, nhánh cận, tham lam,...Những chiến lược nói trên thực ra sẽ không xuất hiện quá nhiều trong những cuộc thi lập trình, và cũng không phải là cách hay để giải quyết bài toán, vì nhiều lí do:

• Trong các cuộc thi lập trình, mỗi bài tập đều bị giới hạn thời gian rất chặt. Giải pháp quay lui hay nhánh cận mặc dù luôn luôn cho ra kết quả đúng, nhưng thời gian thực thi quá lớn, nên chỉ có thể lấy được số điểm rất ít.
• Giải pháp Tham lam mặc dù thời gian thực thi khá nhanh, nhưng kết quả lại không phải luôn luôn chính xác.

Còn một giải pháp nữa mà tôi cũng đã giới thiệu tới các bạn, đó là Chia để trị (Divide and Conquer). Tư tưởng của phương pháp này là chia nhỏ bài toán thành các bài toán con đơn giản hơn, tìm lời giải của chúng, cuối cùng kết hợp nghiệm của các bài toán con lại thành nghiệm của bài toán ban đầu. Giải thuật đệ quy cũng được thiết kế dựa trên nguyên lí này. Tuy nhiên, trong quá trình chia nhỏ bài toán lớn, sẽ có rất nhiều bài toán con bị lặp lại, gây ra các bước tính toán thừa thãi. Phương pháp Quy hoạch động ra đời chính là để giải quyết việc đó.

Mặc dù nghe có vẻ đơn giản, nhưng thực tế Quy hoạch động lại là phương pháp tốn rất nhiều giấy mực của các chuyên gia Tin học, cũng như khiến cho những người học lập trình cảm thấy rất đau đầu. Nhưng tỉ lệ thuận với sự phức tạp của nó, thì khả năng ứng dụng của phương pháp này trong các bài toán cũng vô cùng to lớn. Cụ thể ra sao, chúng ta hãy cùng tìm hiểu thông qua bài viết này.

II. Các khái niệm căn bản

1. Công thức truy hồi

Đây là một khái niệm khá quen thuộc với các bạn học sinh giỏi Toán. Đây là một chủ đề quan trọng của Lý thuyết tổ hợp, có nhiều ứng dụng trong các bài toán đếm, đồng thời là một công cụ vô cùng hữu hiệu để giải các bài toán có bản chất Đệ quy.

Lấy một ví dụ đơn giản, dãy số Fibonacci được định nghĩa đệ quy như sau:

$$\begin{cases}f_0 = f_1 = 1. \\ f_i = f_{i - 1} + f_{i - 2}; \forall i > 1. \end{cases}$$

Trong định nghĩa trên, ta có hai yếu tố cần chú ý:

• $f_0 = f_1 = 1$. Đây là các giá trị cung cấp sẵn của bài toán, hay còn gọi là bài toán cơ sở.
• $f_i = f_{i - 1} + f_{i - 2}$. Đây là công thức để liên hệ giữa phần tử thứ $i$ của dãy số với các phần tử trước nó, hay còn gọi là công thức truy hồi.

Tóm lại, công thức truy hồi là một công thức dùng để liên hệ giữa kết quả của các bài toán con với kết quả của bài toán lớn hơn nó, từ đó tìm ra được lời giải cho bài toán ban đầu. Đây là đặc trưng chỉ xuất hiện trong những bài toán có tính chất đệ quy, nghĩa là lời giải cho bài toán lớn hơn được định nghĩa thông qua lời giải cho bài toán nhỏ hơn nó.

2. Bài toán tối ưu

Bài toán tối ưu là một bài toán có nhiều ứng dụng trong thực tế. Các bạn có lẽ đã nghe nhiều tới khái niệm này trong các phương pháp trước đó, nhưng chỉ là một cách đại thể. Bài toán tối ưu được định nghĩa chính xác như sau:

Xét bài toán có nghiệm là $X$. Gọi $f(X)$ là một hàm đánh giá độ "tốt" của nghiệm $X;$ còn $(g_1, g_2,\dots, g_n)$ là các hàm điều kiện của bài toán. Nếu như bài toán yêu cầu tìm một nghiệm $X$ sao cho $X$ thỏa mãn tất cả các hàm điều kiện $\big(g_i(X) = \text{true}, \forall i: 1 \le i \le n\big),$ đồng thời $f(X)$ là "tốt nhất", thì bài toán đó gọi là bài toán tối ưu.

III. Phương pháp Quy hoạch động

1. Bài toán con gối nhau và Cấu trúc con tối ưu

Bài toán con gối nhau

Như đã nói, những bài toán có bản chất đệ quy đều có thể giải được bằng phương pháp đệ quy. Hãy lấy luôn ví dụ là bài toán dãy Fibonacci ở trên. Nếu như sử dụng phương pháp đệ quy, ta sẽ cài đặt nó như sau:

Ngôn ngữ C++:

int fibo(int n)
{
    if (n <= 1)
        return n;

    return fibo(n - 1) + fibo(n - 2); 
}

Ngôn ngữ Python:

def fibo(n):
    if n <= 1:
        return n

    return fibo(n - 1) + fibo(n - 2)

Hãy cùng nhìn vào sơ đồ thực thi của lời giải đệ quy trên, với $n = 5$:

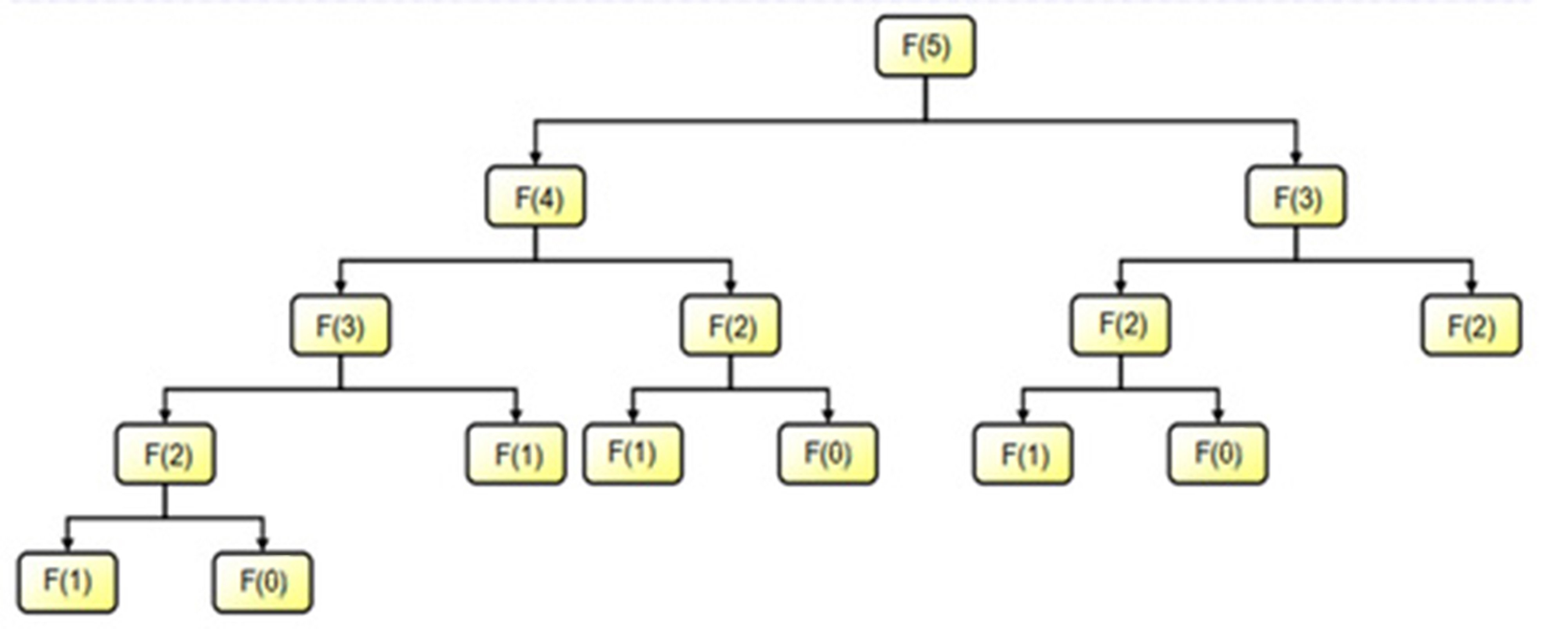
Ta thấy để tính được bài toán $fibo(5),$ chương trình phải tính lại $1$ lần $fibo(4), 2$ lần $fibo(3), 3$ lần $fibo(2), 5$ lần $fibo(1)$ và $3$ lần $fibo(0)$. Những bài toán trùng lặp đó gọi là bài toán con gối nhau, chúng chính là tác nhân chính khiến cho giải thuật đệ quy chạy rất chậm, vì việc tính toán phải thực hiện lại ngay cả khi bài toán đã có đáp số rồi!

Cấu trúc con tối ưu

Một bài toán tối ưu được gọi là thỏa mãn tính chất có "cấu trúc con tối ưu" khi và chỉ khi, lời giải tối ưu cho bài toán đó có thể thu được bằng cách sử dụng lời giải tối ưu của các bài toán con của nó.

Lấy một ví dụ đơn giản, bạn cần tìm một đường đi ngắn nhất từ nhà tới ga Hà Nội, và bạn biết rằng để tới được ga Hà Nội, thì chắc chắn phải đi qua phố Lê Duẩn. Vậy bạn có thể tìm một đường đi ngắn nhất từ nhà tới phố Lê Duẩn, rồi từ phố Lê Duẩn đi tới ga Hà Nội. Việc chia nhỏ các bài toán sẽ lại tiếp tục từ phố Lê Duẩn, cho tới khi tới được một địa điểm nào đó mà bạn đã biết chắc chắn đường đi ngắn nhất từ nhà mình tới địa điểm đó. Có thể nói, trong cuộc sống thường ngày chúng ta cũng hay tư duy theo cấu trúc con tối ưu, chứ không chỉ trong toán học!

2. Phương pháp Quy hoạch động

Quy hoạch động là phương pháp ra đời vào năm 1953, được sáng tạo bởi nhà Toán học người Mỹ Richard Bellman (1920 - 1984) để làm giảm thời gian chạy của các bài toán có tính chất của những bài toán con gối nhau và cấu trúc con tối ưu.

Hai dạng thường gặp nhất của các bài toán giải bằng quy hoạch động là:

• Bài toán đếm có bản chất đệ quy.
• Bài toán tối ưu có bản chất đệ quy.

Tư tưởng chủ đạo của phương pháp này vẫn là "chia để trị", tuy nhiên, sự khác biệt là ở phương pháp Quy hoạch động, những bài toán con gối nhau xuất hiện trong quá trình phân rã bài toán lớn sẽ được lưu lại hết lời giải trong một bảng phương án, thay vì tính toán lại nhiều lần. Sau đó, các lời giải này sẽ được kết hợp lại với nhau bằng công thức truy hồi để tạo thành kết quả của bài toán lớn.

Lấy ví dụ, bài toán Fibonacci thay vì giải bằng phương pháp đệ quy, thì ta có thể lưu lại kết quả của từng bài toán $fibo(i)$ bằng một mảng $f[i],$ rồi sử dụng kết quả đã tính để tạo ra số fibonacci tiếp theo.

Cài đặt C++:

int fibo(int n)
{
    int f[n + 1];
    f[0] = f[1] = 1;
	
    for (int i = 2; i <= n; ++i)
        f[i] = f[i - 1] + f[i - 2];
		
    return f[n];
}

Cài đặt Python:

def fibo(n):
    f = [0] * (n + 1)
	
    f[0] = f[1] = 1
    for i in range(2, n + 1):
        f[i] = f[i - 1] + f[i - 2]
	
    return f[n]

Với phương pháp này, mỗi giá trị Fibonacci được đảm bảo chỉ phải tính một lần duy nhất, khác hẳn với phương pháp đệ quy đã trình bày ở bên trên. Nhờ thế, thuật toán sẽ thực thi rất hiệu quả về mặt thời gian.

Bảng dưới đây sẽ so sánh những điểm khác biệt giữa hai phương pháp Đệ quy và Quy hoạch động:

Tựu chung lại, một bài toán Quy hoạch động sẽ được giải qua ba bước:

• Bước $1$: Giải tất cả các bài toán cơ sở, lưu sẵn vào bảng phương án.
• Bước $2$: Sử dụng công thức truy hồi, phối hợp lời giải của các bài toán con, từ đó tìm ra lời giải của bài toán lớn và tiếp tục lưu vào bảng phương án. Thực hiện như vậy tới khi tìm ra lời giải của bài toán ban đầu.
• Bước $3$: Dựa vào bảng phương án, truy vết tìm ra nghiệm tối ưu của bài toán.

Ngoài ra, các bạn cũng cần ghi nhớ một số khái niệm khi học về phương pháp Quy hoạch động:

• Bài toán giải theo phương pháp Quy hoạch động gọi là Bài toán Quy hoạch động.
• Công thức phối hợp nghiệm của các bài toán con để có nghiệm của bài toán lớn gọi là Công thức truy hồi của Quy hoạch động.
• Tập các bài toán nhỏ nhất có ngay lời giải để từ đó tìm cách giải quyết các bài toán lớn hơn gọi là Cơ sở Quy hoạch động.
• Không gian lưu trữ lời giải các bài toán con để tìm cách phối hợp chúng gọi là Bảng phương án của Quy hoạch động.

Bây giờ, hãy cùng xét một số bài toán minh họa để hiểu rõ hơn về phương pháp này!

IV. Một số bài toán minh họa

1. Lát gạch

Đề bài

Một hành lang có kích thước $2 \times n$ ô gạch gần được lát gạch hoa. Chẳng hạn với $n = 7,$ hành lang được biểu diễn như hình vẽ dưới đây:

Yêu cầu: Hãy đếm số cách lát các viên gạch có kích thước $2 \times 1$ sao cho lát kín được hành lang?

Input:

• Một dòng duy nhất chứa số nguyên dương $n$ - độ dài hành lang.

Ràng buộc:

• $1 \le n \le 10^6$.

Output:

• Số nguyên duy nhất là số cách lát gạch thỏa mãn. In ra phần dư của kết quả sau khi chia cho $10^9 + 7$.

Sample Input:

4

Sample Output:

5

Phân tích ý tưởng

Đầu tiên, ta nhận thấy hai trường hợp $n = 1$ và $n = 2$ có thể giải ngay lập tức:

• Nếu $n = 1,$ chỉ có một cách duy nhất để lát gạch là sử dụng một viên gạch đặt theo chiều dọc.
• Nếu $n = 2,$ có hai cách để lát gạch là đặt hai viên gạch theo chiều dọc hoặc chiều ngang.

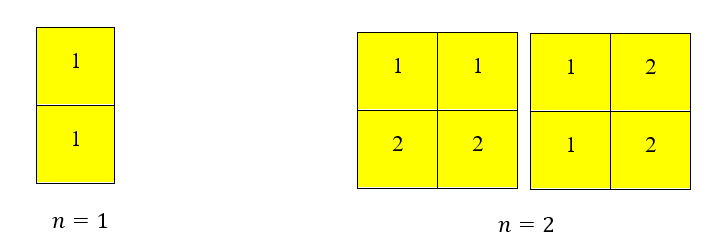
Đặt $dp[i]$ là số cách lát gạch tính đến cột thứ $i,$ thì ta đã biết trước $dp[1] = 1$ và $dp[2] = 2$. Bây giờ, để lát kín cột thứ $i$ của hàng lang, ta có hai phương án như hình bên dưới:

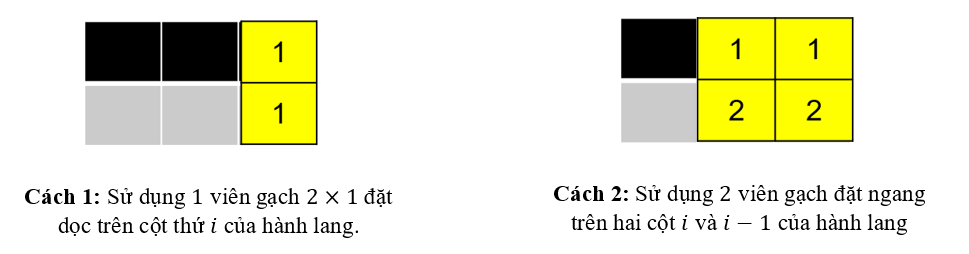
Đối với cách lát gạch thứ nhất, thì tổng số cách lát tính tới cột thứ $i$ sẽ bằng tổng số cách lát tính tới cột thứ $i - 1$. Còn đối với cách lát gạch thứ hai, thì tổng số cách lát tính tới cột thứ $i$ sẽ bằng tổng số cách lát tính tới cột thứ $i - 2$.

Từ đây, ta rút ra công thức truy hồi:

$$dp[i] = dp[i - 1] + dp[i - 2]; \forall i \ge 3$$

Đây là một bài toán đếm có bản chất đệ quy. Nếu sử dụng phương pháp đệ quy, thì giống như bài toán dãy Fibonacci, sẽ có rất nhiều giá trị $dp[i]$ bị tính lại, dẫn đến thời gian thực hiện không thể trong $1$ giây được. Giải pháp là sử dụng một mảng $dp[]$ để lưu lại kết quả sau mỗi lần tính, để đảm bảo mỗi giá trị $dp[i]$ chỉ phải tính một lần duy nhất.

Lưu ý đề bài yêu cầu in ra kết quả sau khi chia lấy dư cho $10^9 + 7$. Đối với C++, cần thực hiện phép chia dư liên tục để tránh bị tràn số.

Cài đặt

Cài đặt C++:

#include <bits/stdc++.h>

using namespace std;

const long long mod = 1e9 + 7;

main()
{
    int n;
    cin >> n;
	
    long long dp[n + 1];
    dp[1] = 1;
    dp[2] = 2;
	
    for (int i = 3; i <= n; ++i)
        dp[i] = (dp[i - 1] + dp[i - 2]) % mod;
		
    cout << dp[n];
	
    return 0;
}

Cài đặt Python:

if __name__ == '__main__':
    n = int(input())
	
    dp = [0] * (n + 1)
    dp[1] = 1
    dp[2] = 2
	
    for i in range(3, n + 1):
        dp[i] = dp[i - 1] + dp[i - 2]
    
    mod = 10 ** 9
    print(dp[n] % mod)

Đánh giá độ phức tạp

Mỗi giá trị $dp[i]$ chỉ được tính duy nhất một lần, do đó chương trình sẽ có độ phức tạp là $O(n)$.

2. Dãy con tăng dài nhất

Đề bài

Cho dãy số nguyên gồm $n$ phần tử $a_1,a_2,…,a_n$. Một dãy con của dãy số là một cách chọn ra $k$ phần tử bất kỳ của dãy số, với $k \le n$. Dãy con đơn điệu tăng gồm $k$ phần tử là dãy con $a_{i_1}, a_{i_2}, \dots, a_{i-k}$ thỏa mãn $a_{i_1} < a_{i_2} < \dots <a_{i_k}$.

Yêu cầu: Hãy tìm dãy con đơn điệu tăng dài nhất của dãy đã cho?

Input:

• Dòng đầu tiên chứa số nguyên dương $n$ - độ dài dãy số.
• Dòng thứ hai chứa $n$ số nguyên $a_1, a_2, \dots, a_n$ phân tách nhau bởi dấu cách - các phần tử của dãy ban đầu.

Ràng buộc:

• $1 \le n \le 1000$.
• $|a_i| \le 10^6; \forall i: 1 \le i \le n$.

Output:

• Dòng đầu tiên chứa một số nguyên là độ dài của dãy con tăng dài nhất tìm được.
• Dòng thứ hai chứa dãy con đó. Nếu tìm được nhiều dãy thì in ra một dãy bất kỳ.

Sample Input:

5
1 4 2 3 2

Sample Output:

3
1 2 3

Phân tích ý tưởng

Hãy gọi $dp[i]$ là độ dài của dãy con tăng dài nhất kết thúc tại phần tử $a_i$.

Có một nhận xét rằng, trước khi tính $dp[i],$ nếu như ta đã biết được các $dp[0], dp[1], \dots, dp[i - 1]$ thì ta hoàn toàn có thể tính được $dp[i]$ bằng cách lựa chọn một vị trí $j$ phía trước nó để ghép $a_i$ vào cuối dãy con đơn điệu tăng kết thúc tại $a_j$. Điều quan trọng là lựa chọn dãy nào cho tốt nhất?

Nhận xét trên khiến ta rút ra được bài toán này là một bài toán thỏa mãn cấu trúc con tối ưu, và nó lại có bản chất đệ quy. Dĩ nhiên, muốn tạo được dãy con tăng kết thúc tại $a_i$ dài nhất, thì ta cần lựa chọn dãy con tăng dài nhất kết thúc tại một vị trí $a_j$ phía trước $a_i,$ và $a_j$ phải nhỏ hơn $a_i$ (để đảm bảo tính tăng). Từ đây ta rút ra công thức:

$$dp[i] = \text{max}\big(dp[j]\big) + 1; \forall j: 1 \le j < i \text{ and } a_j < a_i$$

Kết quả cuối cùng tất nhiên phải là $\text{max}(dp[i]); \forall i: 1 \le i \le n$.

Để truy vết tìm ra dãy con tăng dài nhất, ta sử dụng thêm một mảng $trace[i]$ để lưu lại vị trí của phần tử $a_j$ liền trước $a_i$ trong dãy con tăng dài nhất kết thúc tại $a_i$. Mỗi khi ta tính được $dp[i] = dp[jmax] + 1,$ thì hãy lưu $trace[i] = jmax$. Sau đó, quá trình truy vết diễn ra như sau:

• Gọi $\text{best}$ là vị trí có $dp[\text{best}]$ lớn nhất. Phần tử cuối cùng được chọn của dãy sẽ là $a[\text{best}]$.
• Phần tử áp chót trong dãy được chọn là $a\big[trace[\text{best}]\big]$.
• Phần tử liền trước phần tử áp chót trong dãy được chọn là $a\Big[trace\big[trace[\text{best}\big]\Big]$. $\dots$

Vậy ta có thể liên tục thực hiện gán $\text{best} = trace[\text{best}]$ rồi ghi nhận phần tử ở vị trí $\text{best},$ cho tới khi $\text{best} = 0$ thì hoàn thành quá trình truy vết.

Cài đặt

Cài đặt C++:

#include <bits/stdc++.h>

using namespace std;

// Nhập dữ liệu.
void enter(int &n, vector < int > &a)
{
    cin >> n;

    a.resize(n + 1);
    for (int i = 1; i <= n; ++i)
        cin >> a[i];
}

// Truy vết tìm ra độ dài dãy con tăng dài nhất.
// và tìm ra một dãy con tăng dài nhất.
void trace_back(int n, vector < int > &a, vector < int > &dp, vector < int > &trace)
{
    // Chọn ra vị trí best_pos có dp tại đó lớn nhất.
    int best_pos = 0;
    for (int i = 1; i <= n; ++i)
        if (dp[i] > dp[best_pos])
            best_pos = i;

    cout << dp[best_pos] << endl;

    vector < int > lis_elements;
    while (best_pos)
    {
        lis_elements.push_back(a[best_pos]);
        best_pos = trace[best_pos];
    }

    for (int i = lis_elements.size() - 1; i >= 0; --i)
        cout << lis_elements[i] << ' ';
}

// Sử dụng công thức truy hồi để tính bảng phương án.
void solution(int n, vector < int > &a)
{
    vector < int > dp(n + 1), trace(n + 1);

    for (int i = 1; i <= n; ++i)
    {
        // Chọn vị trí jmax tốt nhất để nối a[i] vào sau.
        int jmax = 0;
        for (int j = 1; j < i; ++j)
            if (dp[j] > dp[jmax] && a[j] < a[i])
                jmax = j;

        dp[i] = dp[jmax] + 1; // Cập nhật dp[i].
        trace[i] = jmax; // Lưu vết phần tử đứng trước a[i] là a[jmax].
    }

    trace_back(n, a, dp, trace);
}

main()
{
    int n;
    vector < int > a;

    enter(n, a);
    solution(n, a);

    return 0;
}

Cài đặt Python:

import sys


# Truy vết và in ra kết quả.
def trace_back(n, a, dp, trace):
    # Chọn ra vị trí best_pos có dp tại đó lớn nhất.
    best_pos = 1
    for i in range(2, n + 1):
        if dp[i] > dp[best_pos]:
            best_pos = i
			
    print(dp[best_pos])
	
    # Tìm ra dãy con tăng dài nhất có phần tử kết thúc là a[best_pos].
    lis_elements = []
    while best_pos != 0:
        lis_elements.append(a[best_pos])
        best_pos = trace[best_pos]
	
    lis_elements.reverse()
	
    print(lis_elements)


# Tính bảng phương án bằng công thức truy hồi.
def solution(n, a):
    trace, dp = [0] * (n + 1)
	
    for i in range(1, n):
	
        # Chọn vị trí jmax tốt nhất để nối a[i] vào sau.
        jmax = 0
        for j in range(1, i - 1):
            if dp[j] > dp[jmax] and a[j] < a[i]:
                jmax = j
				
        dp[i] = dp[jmax] + 1  # Cập nhật dp[i].
        trace[i] = jmax  # Lưu vết phần tử liền trước a[i] là a[jmax].
	
    trace_back(n, a, dp, trace)
	
	
if __name__ == '__main__':
    n = int(input())
    
    a = [0] * (n + 1)
    for i in range(1, n + 1):
        a[i] = int(input())
	
    solution(n, a)

Đánh giá độ phức tạp

Với mỗi giá trị $dp[i],$ ta cần thực hiện lại một vòng lặp với $i$ thao tác so sánh và kiểm tra để chọn ra vị trí $j$ thỏa mãn $dp[j]$ lớn nhất và $a[j] < a[i]$. Vì thế số lần lặp là $\frac{n \times (n + 1)}{2},$ tương ứng với độ phức tạp là $O(n^2)$.

V. Tổng kết

Như vậy, trong bài viết này, chúng ta đã cùng nhau tìm hiểu về những khái niệm cơ bản nhất của phương pháp Quy hoạch động. Hy vọng các bạn đã có thể hình dung được cách hoạt động của phương pháp sau khi đọc những bài toán ví dụ tôi đưa ra.

Ngoài ra, như đã nói ở trên, phương pháp Quy hoạch động thường dùng để giải hai dạng bài toán:

• Bài toán đếm có bản chất đệ quy.
• Bài toán tối ưu có bản chất đệ quy.

Vì vậy, nếu như các bạn gặp phải một bài toán yêu cầu đếm một đại lượng nào đó, hoặc yêu cầu tìm ra một kết quả lớn nhất hay nhỏ nhất, thì có nhiều khả năng đó là một bài toán giải bằng phương pháp Quy hoạch động. Điều cần quan tâm cuối cùng là bài toán đó có bản chất đệ quy hay không? Để kiểm tra điều này, các bạn có thể thử suy nghĩ giải bài toán đó bằng Đệ quy (với kích thước nhỏ thì bài toán Quy hoạch động hoàn toàn giải được bằng Đệ quy), rồi mới quyết định có sử dụng Quy hoạch động hay không.

Đôi khi những bài toán có yêu cầu tìm kết quả lớn nhất hay nhỏ nhất lại là một bài toán sử dụng Tìm kiếm nhị phân thay vì Quy hoạch động, vì thế các bạn cần phân biệt rõ điều kiện cần và đủ của hai phương pháp này, tránh gây ra nhầm lẫn khi giải các bài toán.

Cuối cùng, hãy luyện tập thật nhiều!

VI. Tài liệu tham khảo

• Competitive Programming 3 - Steven Halim & Felix Halim.
• https://www.geeksforgeeks.org/optimal-substructure-property-in-dynamic-programming-dp-2/.
• https://www.geeksforgeeks.org/overlapping-subproblems-property-in-dynamic-programming-dp-1/.
• Sách Giải thuật và Lập trình - thầy Lê Minh Hoàng.
• Tài liệu giáo khoa chuyên Tin quyển 1 - thầy Hồ Sĩ Đàm.