Chào mọi người, trong Series Machine Learning From Scratch này mình và các bạn sẽ cùng đi triển khai các thuật toán cơ bản trong học máy để cùng hiểu rõ hơn bản chất của các thuật toán này nhé.

1. Vì sao cần giảm chiều dữ liệu?

Như mọi người đã biết, trong các bài toán học máy thì dữ liệu có kích thước rất lớn. Máy tính có thể hiểu và thực thi các thuật toán trên dữ liệu này, tuy nhiên đối với con người để "nhìn" dữ liệu nhiều chiều thật sự là rất khó. Vì vậy bài toán giảm chiều dữ liệu ra đời giúp đưa ra cái nhìn mới cho con người về dữ liệu nhiều chiều. Ngoài để trực quan dữ liệu, các phương pháp giảm chiều dữ liệu còn giúp đưa dữ liệu về một không gian mới giúp khai phá các thuộc tính ẩn mà trong chiều dữ liệu ban đầu không thể hiện rõ, hoặc đơn giản là giảm kích thước dữ liệu để tăng tốc độ thực thi cho máy tính. Ví dụ về tập dữ liệu huyền thoại Iris bao gồm 4 thuộc tính và 3 nhãn tương ứng với 3 loài hoa. Rất khó để có thể nhận biết rằng 4 thuộc tính này có phân tách với nhau theo mỗi loài hay không vì cần biểu diễn không gian này trên dữ liệu 4 chiều. Vì vậy, thuật toán giảm chiều dữ liệu giúp đưa về không gian 2 chiều để dễ dàng trực quan hóa trên hệ toạn độ Oxy, đổi lại là chúng ta phải chấp nhận mất mát đi một lượng thông tin. Và đây là kết quả:

Nhìn vào đây chúng ta có thể dễ dàng phân tích hơn, có thể thấy lớp nào dễ nhầm lẫn với nhau, mức độ tách biệt giữa các lớp,...

2. Thuật toán PCA (Principal component analysis)

Về mặt ý tưởng, thuật toán PCA tìm một hệ không gian mới và tối đa hóa phương sai dữ liệu của không gian mới đó. Sau đó lựa chọn ra n chiều có phương sai lớn nhất (giả thuyết rằng dữ liệu càng phân tán, phương sai càng lớn thì càng có giá trị)

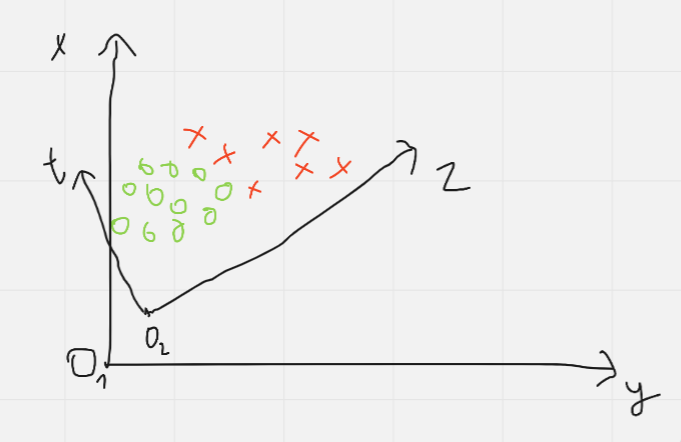
Hình trên đây thể hiện được giá trị của phương sai, khi mà đối với không gian ban đầu ($O_1$ xy) thì phần overlape của 2 lớp khi ánh xạ lên mỗi trục là khá lớn. Khi đó không gian mới ($O_{2}$ zt) được cực đại hóa phương sai cho trục $O_2$ z nên khi ánh xạ lên đây các lớp sẽ tách biệt với nhau khá rõ. Để tìm được không gian mới, PCA đi tìm các trị riêng của ma trận hiệp phương sai của dữ liệu đầu vào. Các trị riêng thể hiện phương sai của chiều dữ liệu mới, các vector riêng ứng với trị riêng đó tương ứng với một không gian dữ liệu mới. Vậy nên sau bước này chúng ta chọn các vector riêng ứng với các trị riêng có giá trị lớn nhất để được một không gian mới được cực đại hóa phương sai. Chi tiết về phần đại số mọi người có thể đọc thêm tại đây

Để làm được việc này, thuật toán PCA cần thực hiện qua các bước:

• Step 1: Chuẩn bị dữ liệu cần giảm chiều là X với kích thước (n_sample, n_feature), tương ứng mỗi hàng là 1 mẫu dữ liệu có n_feature thuộc tính
• Step 2: Trừ mỗi điểm dữ liệu cho vector kỳ vọng: $X_k$ = $X_k$ - $X_{mean}$ với k = 1..n_sample và $X_{mean}$ là vector trung bình của tất cả các điểm dữ liệu
• Step 3: Tính ma trận hiệu phương sai : S = $\frac{1}{n-sample}*X^T*X$
• Step 4: Tìm trị riêng, vector riêng của ma trận S
• Step 5: Lấy k trị riêng có giá trị lớn nhất, tạo ma trận U với các hàng là các vector riêng ứng với k trị riêng đã chọn
• Step 6: Ánh xạ không gian ban đầu sang không gian k chiều: $X_{new}$ = X*U
• Note: Nếu không hiểu phép nhân ở Step 6 bạn có thể lấy từng mẫu dữ liệu nhân với từng vector riêng, khi đó mỗi mẫu dữ liệu ban đầu sẽ được nhân với k vector nên sẽ có k chiều.

3. Python implement:

Giả sử đã có ma trận dữ liệu X, mình sẽ thực hiện lần lược từ Step 2 đến Step 6 cho mọi người tiện theo giỏi nhé:

• Step 2: Tính vector trung bình, sau đó trừ các điểm dữ liệu cho vector đó

mean = np.mean(X, axis=0)
X = X - mean

• Step 3: Tìm ma trận hiệp phương sai

cov = X.T.dot(X) / X.shape[0]

• Step 4: Tính trị riêng, vector riêng

eigen_values, eigen_vectors, = np.linalg.eig(cov)

• Step 5: Ở bước này mình sẽ lấy chỉ số index của trị riêng từ lớn đến nhỏ, rồi chọn k vector riêng tạo ma trận U tương ứng với k index đã tìm được

select_index = np.argsort(eigen_values)[::-1][:k]
U = eigen_vectors[:, select_index]

• Step 6: Ánh xạ dữ liệu sang không gian mới

X_new = X.dot(U)

Và đây là toàn bộ code mình chạy thử trên tập dữ liệu Iris, mọi người có thể tìm thấy tập dữ liệu này trên Google nhé

import numpy as np
import pandas as pd
fỏm matplotlib import pyplot as plt

class PCA:
  def __init__(self, n_dimention: int):
    self.n_dimention = n_dimention

  def fit_transform(self, X):
    mean = np.mean(X, axis=0)
    X = X - mean
    cov = X.T.dot(X) / X.shape[0] 
    eigen_values, eigen_vectors, = np.linalg.eig(cov)
    select_index = np.argsort(eigen_values)[::-1][:self.n_dimention]
    U = eigen_vectors[:, select_index]
    X_new = X.dot(U)
    return X_new
    
if __name__ == "__main__":
  df = pd.read_csv(r"/content/iris.csv")
  X = df[["sepal_length",	"sepal_width",	"petal_length",	"petal_width"]].to_numpy()
  Y = df["species"].to_numpy()

  pca = PCA(n_dimention=2)
  new_X = pca.fit_transform(X)
  
  for label in set(Y):
    X_class = new_X[Y == label]
    plt.scatter(X_class[:, 0], X_class[:, 1], label=label)

  plt.legend()

Và đây là kết quả khi chuyển tập dữ liệu Iris từ 4 chiều về 2 chiều nhé

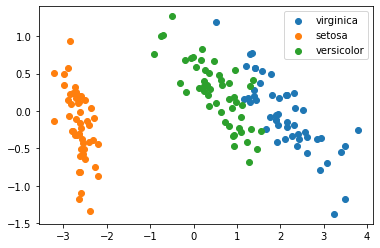
4. Kết luận

Trong bài viết này mình và các bạn đã cùng tìm hiểu qua về cách mà thuật toán PCA hoạt động trong bài toán giảm chiều dữ liệu củng như cách triển khai nó bằng ngôn ngữ Python. Cảm ơn các bạn đã đọc bài viết và nhớ Upvote cho mình nếu thấy bài viết hữu ích nhé.😀

Tài liệu tham khảo:

• Bài 27: Principal Component Analysis (phần 1/2)