Mạng lan truyền ngược
Bài đăng này đã không được cập nhật trong 4 năm
Mạng lan truyền ngược hay còn được gọi là mạng phản hồi (truy hồi) được sử dụng khá phổ biến trong các model của AI hiện nay như DeepID-X hay CNN và đã được ứng dụng trong thực tế như: dùng làm bộ nhớ địa chỉ hóa nội dung; dùng làm các bộ tối ưu; đặc biệt thành công là thực hiện để sản xuất các phần cứng máy tính kiểu tương tự, điển hình gồm: Mạng Hopfield rời rạc (1982); Mạng Hopfield liên tục (1984); Mạng liên kết hai chiều BAM (thực chất là hai mạng Hopfield đấu phản hồi); mạng Cohen-Grossberg (thực chất là khái quát hóa mạng Hopfield liên tục thành định lý Cohen-Grossberg, nhưng rất khó thực hiện trong kỹ thuật); Mạng neraul tế bào do Chu đề xuất và đã chế tạo thành máy tính đa năng hai chiều (thực chất là mạng nơ ron hai chiều của mạng Hopfield)… Tuy nhiên, dù nó được ứng dụng khá nhiều, bạn có thực sự biết về Mạng lan truyền ngược để có thể chọn được phương pháp tốt nhất cho bài toán của mình khi xây dựng model riêng cho mỗi trường hợp nhất định? Hôm nay mình xin giới thiệu một số mạng neraul phản hồi có tính ổn định của các mạng điển hình nhất là Mạng Hopfield rời rạc (1982); Mạng Hopfield liên tục (1984).
1. Mạng Hopfield rời rạc
Xét mạng Hopfield rời rạc (năm 1982). Phương trình mô tả luật tác động:
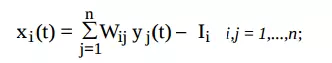
Luật cập nhật đầu ra:
nếu xi(t) khác 0, i = p nếu xi(t) = 0, i khác p
Hàm quan hệ vào ra là hàm phi tuyến bước nhảy
$ g(xi(t)) = 1 $ nếu xi(t) > 0
$\quad\quad \quad= 0 $ nếu xi(t) < 0
Luật cập nhật trọng liên kết theo luật Hebb tương quan:
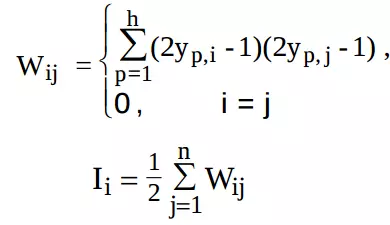 Trong đó, $ xi(t)$: tổng của tất cả các đầu vào; : đầu ra của nơ ron; : là trọng liên kết phản hồi từ nơ ron i tới nơ ron j ; : hằng số của neural i; h là số mẫu được cất giữ; n là số neural; p là phần tử thứ p đang tác động.
Hopfield cũng nêu hàm năng lượng mạng (hay hàm thế năng):
Trong đó, $ xi(t)$: tổng của tất cả các đầu vào; : đầu ra của nơ ron; : là trọng liên kết phản hồi từ nơ ron i tới nơ ron j ; : hằng số của neural i; h là số mẫu được cất giữ; n là số neural; p là phần tử thứ p đang tác động.
Hopfield cũng nêu hàm năng lượng mạng (hay hàm thế năng):
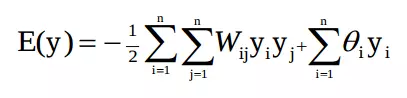 Nếu Wij = 0 và Wij = Wji thì mỗi thay đổi không đồng bộ của yp năng lượng sẽ giảm phù hợp theo:
Nếu Wij = 0 và Wij = Wji thì mỗi thay đổi không đồng bộ của yp năng lượng sẽ giảm phù hợp theo:
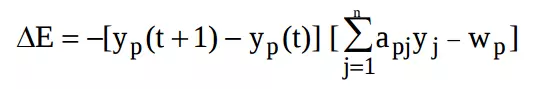
2 Mô hình mạng Hopfield liên tục chuẩn
Hopfield (1984) đa ra mô hình mạng mô tả bằng tập các phương trình vi phân
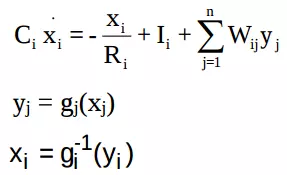 Trong đó, Ci và Ri là các hằng số; Ii là ngưỡng; Wij là trọng liên kết giữa phần tử neural thứ j với neural thứ i; xi là trạng thái neural thứ i.
Hopfield nêu hàm Liapunov với dạng sau:
Trong đó, Ci và Ri là các hằng số; Ii là ngưỡng; Wij là trọng liên kết giữa phần tử neural thứ j với neural thứ i; xi là trạng thái neural thứ i.
Hopfield nêu hàm Liapunov với dạng sau:
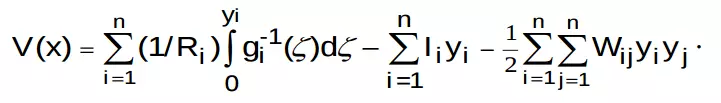
a) Ứng dụng mạng Hopfield cho các bài toán tối ưu
Để giải quyết các vấn đề tối ưu óa thì trong mạng hopfield, các hàm năng lượng được sử dụng tương đương như hàm mục tiêu để mà tối thiểu hoá. Việc tìm hàm tối thiểu trong mạng Hopfield chính là tìm lời giải cho các vấn đề tối ưu. Kết quả là phải đưa ra một vấn đề tối ưu với một hàm mục tiêu chính xác mà nó có thể được dùng để cấu thành một mạng hopfield, đặc biệt là tìm các trọng (weight) của chúng. Khi ta sử dụng mạng noron để giải quyết các vấn đề tối ưu, thì phải xây dựng chính xác từng loại thuật toán song song phù hợp với lời giải đó.
Ví dụ. Thiết kế bộ chuyển đổi A/D 4 bít mà sử dụng mạng Hopfield đơn liên tục
Mục đích là chuyển đổi từ một giá trị đầu vào liên tục là x (0< x <15) và đầu ra là $ y = [y3 , y2 , y1 , yo]^T $ với yi trong khoảng {0,1}; để giá trị thập phân của $ 8y3 +4 y2 +2 y1 + yo $ và giá trị của x được gần nhau nếu có thể.
Sai số của bộ chuyển đổi A/D
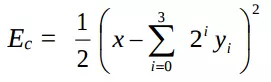 Rõ ràng là tối thiểu hoỏ hàm năng lượng tương đương với việc tối thiểu hoá sai số chuyển đổi của bộ chuyển đổi A/D.
Mục đích là phải xây dựng mạng Hopfield liên tục có 4 nút với hàm một hàm kích hoạt để tối thiểu hoá.
Để phục vụ cho mục đích này, chúng ta phải tìm ra các thông số chính xác, gồm các trọng và đầu vào mở rộng của mạng Hopfied. Việc này có thể được thực hiện được bằng cách so sánh giữa Ec và Eq (hàm năng lượng của mạng Hopfield liên tục).
Tuy vậy, trong biểu thức Ec có với hệ số khác 0 thì cũng làm cho wii trong mạng Hopfield khác không. Sự mâu thuẫn này được định nghĩa trong mạng Hopfield.
Vì vậy Ea được thêm vào như sau:
Rõ ràng là tối thiểu hoỏ hàm năng lượng tương đương với việc tối thiểu hoá sai số chuyển đổi của bộ chuyển đổi A/D.
Mục đích là phải xây dựng mạng Hopfield liên tục có 4 nút với hàm một hàm kích hoạt để tối thiểu hoá.
Để phục vụ cho mục đích này, chúng ta phải tìm ra các thông số chính xác, gồm các trọng và đầu vào mở rộng của mạng Hopfied. Việc này có thể được thực hiện được bằng cách so sánh giữa Ec và Eq (hàm năng lượng của mạng Hopfield liên tục).
Tuy vậy, trong biểu thức Ec có với hệ số khác 0 thì cũng làm cho wii trong mạng Hopfield khác không. Sự mâu thuẫn này được định nghĩa trong mạng Hopfield.
Vì vậy Ea được thêm vào như sau:
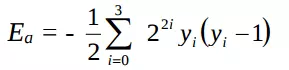 Hàm tổng năng lượng là:
Hàm tổng năng lượng là:
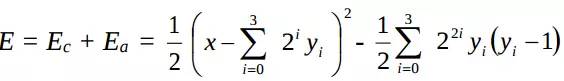 Chú ý rằng Ea không âm và đạt giá trị thấp nhất khi yi=0 hoặc yi=1. Do đó Ea có thể cho trạng thái mạng phải vào các góc của hình sườn khối lập phương (Hypercube) khi E đạt cực tiểu. Ta có hàm năng lượng E của mạng Hopfield liên tục, cứ 1 lớp 4 noron.
Với các đầu vào ngoài $x = [x3, x2, x1 , xo]^T $ và đầu ra
Chú ý rằng Ea không âm và đạt giá trị thấp nhất khi yi=0 hoặc yi=1. Do đó Ea có thể cho trạng thái mạng phải vào các góc của hình sườn khối lập phương (Hypercube) khi E đạt cực tiểu. Ta có hàm năng lượng E của mạng Hopfield liên tục, cứ 1 lớp 4 noron.
Với các đầu vào ngoài $x = [x3, x2, x1 , xo]^T $ và đầu ra
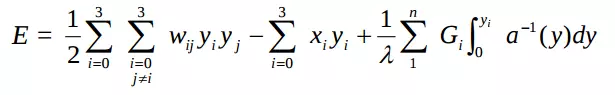 So sánh 2 kết quả trên, ta có:
và với i, j = 0,1,2,3; i khác j
Do đó:
$
W = - \begin{bmatrix}
0 & 2 & 4 & 8 \
2 & 0 & 8 & 16 \
4 & 8 & 0 & 32 \
8 & 16 & 32 & 0
\end{bmatrix}
$ và $ x = \begin{bmatrix}
0,5 & -x \
2 & -2x \
8 & -4x \
32 & -8x
\end{bmatrix} $
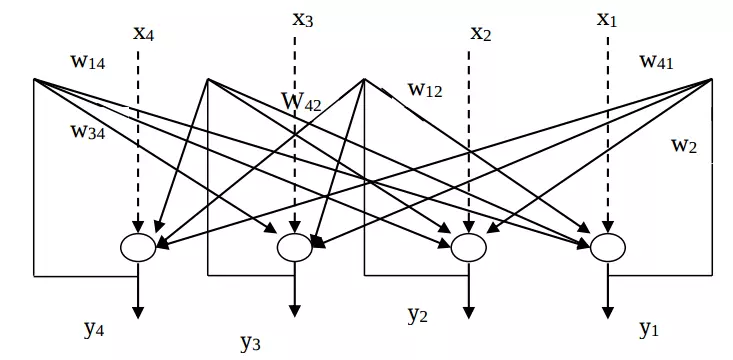
Với ma trận trọng như vậy, ta có sơ đồ mạng Hopfield như sau:
So sánh 2 kết quả trên, ta có:
và với i, j = 0,1,2,3; i khác j
Do đó:
$
W = - \begin{bmatrix}
0 & 2 & 4 & 8 \
2 & 0 & 8 & 16 \
4 & 8 & 0 & 32 \
8 & 16 & 32 & 0
\end{bmatrix}
$ và $ x = \begin{bmatrix}
0,5 & -x \
2 & -2x \
8 & -4x \
32 & -8x
\end{bmatrix} $
Với ma trận trọng như vậy, ta có sơ đồ mạng Hopfield như sau:
 Có hai kiểu bộ nhớ liên kết là bộ nhớ liên kết tự động và bộ nhớ liên kết không đồng nhất (Hereoassociative Memory)
Xem bộ nhớ liên kết như mạng Hopfield với m đầu vào và n đầu ra nhận các giỏ trị 1 hoặc -1
Có hai kiểu bộ nhớ liên kết là bộ nhớ liên kết tự động và bộ nhớ liên kết không đồng nhất (Hereoassociative Memory)
Xem bộ nhớ liên kết như mạng Hopfield với m đầu vào và n đầu ra nhận các giỏ trị 1 hoặc -1
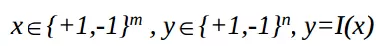 , y=I(x)
Mạng lưu trữ gồm tập p mẫu thông qua các trọng số Wij nhờ thuật toán lưu trữ $W = F(x^r, y^r) $, nếu ta đưa vào mạng mẫu x thì khi mạng ổn định, sẽ cho kết tương ứng giống x nhất trong p mẫu lưu trữ.
Kiểu bộ nhớ tự liên kết:
Kiểu bộ nhớ không đồng nhất: khác
Khái niệm gần nhất “close” có thể xem xét như là một số phép xác định khoảng cách.
Xét khoảng cách của Ơclit và khoảng cách Hamming:
, y=I(x)
Mạng lưu trữ gồm tập p mẫu thông qua các trọng số Wij nhờ thuật toán lưu trữ $W = F(x^r, y^r) $, nếu ta đưa vào mạng mẫu x thì khi mạng ổn định, sẽ cho kết tương ứng giống x nhất trong p mẫu lưu trữ.
Kiểu bộ nhớ tự liên kết:
Kiểu bộ nhớ không đồng nhất: khác
Khái niệm gần nhất “close” có thể xem xét như là một số phép xác định khoảng cách.
Xét khoảng cách của Ơclit và khoảng cách Hamming:
- Khoảng cách Ơclit d của 2 vector $x = (x1, x2,..., xn)^T $ và $x = (x'1, x'2,..., x'k)^T $ được định nghĩa $[ (x1 - x'1)^2 + (x2 - x'2)^2 + ... + (xn - x'n)^2 )^2 ] ^ {1/2} $
- Khoảng cách Hamming HD(x, x’) xác định số lượng các cặp không bằng nhau giữa 2 vector x và x’ Ví dụ: Nếu $ x = (1,1,0,1)^T $ và , khi đó $ HD(x,x^’) = 2 $
b) Ứng dụng mạng Hopfield làm bộ nhớ tự liên kết hồi quy (Bộ nhớ Hopfield)
Đây là mạng Hopfield rời rạc với các ngưỡng và các đầu ngoài vào bằng 0 (chỉ cần thành phần hồi quy (hay đơn giản là phản hồi))
Thuật toán lưu trữ:
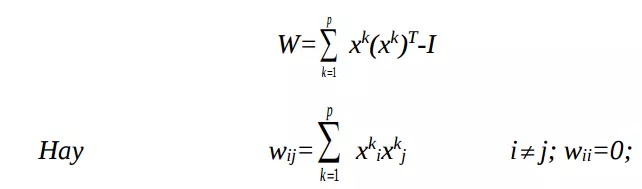 Trong đó, và I là ma trận xác định xấp xỉ
Nếu xi là ma trận nhị phân đơn cực, tức là xi nằm trong khoảng { 0,1}:
Thuật toán lưu trữ:
Trong đó, và I là ma trận xác định xấp xỉ
Nếu xi là ma trận nhị phân đơn cực, tức là xi nằm trong khoảng { 0,1}:
Thuật toán lưu trữ:
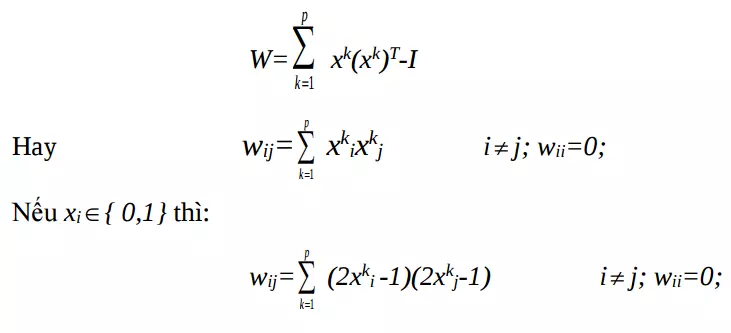 Công thức xác định trên dựa trên luật học Hebbian với trọng số ban đầu là 0. Vì vậy luật học được gọi là luật học kiểu Hebbian hay luật học tích ngoài.
Ta có thể cộng thêm vào bộ nhớ bằng cách tăng ma trận trọng số, cũng như có thể giảm đi. Việc này không bị ảnh hưởng bởi thứ tự lưu trữ các mẫu.
Ví dụ: Xem xét sử dụng bộ nhớ Hopfield để lưu trữ 2 vector và
và $ x^2 = {[-1,1,-1,1]}^T$
Theo luật học trên ta có ma trận trọng số:
$
W = \begin{bmatrix}
0 & -2 & 0 & 0 \
-2 & 0 & 0 & 0 \
0 & 0 & 0 & -2 \
0 & 0 & -2 & 0
\end{bmatrix}
$
Ví dụ trên chỉ ra 1 tính chất quan trọng của bộ nhớ Hopfield đó là sự đầy đủ của một vector lưu trữ cũng là một vector lưu trữ. Bởi vì chúng có cùng một giá trị năng lượng E(x) = . Yếu tố chủ chốt là sự hội tụ tương tự giữa vector đầu ra khởi tạo và x.
Có 2 vấn đề lớn của bộ nhớ Hopfield.
Công thức xác định trên dựa trên luật học Hebbian với trọng số ban đầu là 0. Vì vậy luật học được gọi là luật học kiểu Hebbian hay luật học tích ngoài.
Ta có thể cộng thêm vào bộ nhớ bằng cách tăng ma trận trọng số, cũng như có thể giảm đi. Việc này không bị ảnh hưởng bởi thứ tự lưu trữ các mẫu.
Ví dụ: Xem xét sử dụng bộ nhớ Hopfield để lưu trữ 2 vector và
và $ x^2 = {[-1,1,-1,1]}^T$
Theo luật học trên ta có ma trận trọng số:
$
W = \begin{bmatrix}
0 & -2 & 0 & 0 \
-2 & 0 & 0 & 0 \
0 & 0 & 0 & -2 \
0 & 0 & -2 & 0
\end{bmatrix}
$
Ví dụ trên chỉ ra 1 tính chất quan trọng của bộ nhớ Hopfield đó là sự đầy đủ của một vector lưu trữ cũng là một vector lưu trữ. Bởi vì chúng có cùng một giá trị năng lượng E(x) = . Yếu tố chủ chốt là sự hội tụ tương tự giữa vector đầu ra khởi tạo và x.
Có 2 vấn đề lớn của bộ nhớ Hopfield.
- Thứ nhất, là trạng thái ổn định không định trước gọi là trạng thái ổn định giả tạo nguyên nhân bởi sự tối thiểu các hàm năng lượng thêm vào cái chúng ta cần.
- Thứ hai, tràn bộ nhớ là kết quả của việc khoảng cách Hamming giữa các mẫu lưu trữ nhỏ vì không cung cấp các lỗi và sự phục hồi hiệu quả cho các mẫu lưu trữ. Có thể thấy, có mối quan hệ giữa số lượng các trạng thái giả tạo giảm và kích cỡ (chiều) của vector lưu trữ tăng trên khía cạnh số lượng các vector lưu trữ.
Khả năng lưu trữ của bộ nhớ Hopfield.
Khả năng lưu trữ này có mối quan hệ với kích thước của mạng. Một phép đo hữu hiệu cho việc ước lượng dung lượng của bộ nhớ là bán kính hấp dẫn . Bán kính của một bộ nhớ tự liên kết là: khoảng cách mà mọi vector nằm trong vùng bán kính đó vẫn đạt được trạng thái ổn định. Khoảng cách ở đây thường dùng là khoảng cách Hamming bởi vì giá trị của nó là các số nguyên; nghĩa là, khi đưa vào mẫu x có
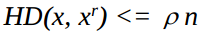 thì ở đầu ra nhận được mẫu lưu trữ
Dung lượng c là số mẫu tối đa có thể được lưu trữ (p <= c) để đảm bảo các mẫu trong bán kính vẫn có thể nhận được đúng. Có thể ước lượng cho bộ nhớ tự liên kết gồm có n neuron (theo McEliece, 1987):
thì ở đầu ra nhận được mẫu lưu trữ
Dung lượng c là số mẫu tối đa có thể được lưu trữ (p <= c) để đảm bảo các mẫu trong bán kính vẫn có thể nhận được đúng. Có thể ước lượng cho bộ nhớ tự liên kết gồm có n neuron (theo McEliece, 1987):

3. Mạng liên kết hai chiều
1. Giới thiệu
Một bộ nhớ liên kết hai chiều (BAM: Bidirectional Associative Memory) có thể lưu trữ một tập các mẫu như các bộ nhớ. Khi ta đưa vào bộ nhớ liên kết một mẫu, nó sẽ trả lại kết quả gần với giá trị tương ứng của mẫu với mẫu đưa vào. Vì vậy, việc xác định thông qua các mẫu với các thông tin cần nhớ. Các mẫu được nhớ vào và gọi ra theo nội dung của nó, nên nó được gọi là bộ nhớ nội dung địa chỉ hoá, khác với bộ nhớ truyền thống của máy tính số là bộ nhớ địa chỉ-địa chỉ hoá. Bộ nhớ liên kết chính là một dạng của mạng Hopfield.
2. Bộ nhớ liên kết 2 chiều sử dụng BAM
BAM là loại bộ nhớ hồi quy liên kết không đồng nhất gồm có 2 lớp và có thể coi như là một sự mở rộng của mạng Hopfield. Nó thực thi việc tìm kiếm xuôi và ngược trong các bộ lưu trữ các tác nhân đáp ứng liên kết. Sau đây là cấu trúc của bộ nhớ BAM rời rạc. Khi các noron nhớ được kích hoạt bởi vector khởi tạo X tạo đầu vào. Khi đó mạng tiến tới có 2 phần trạng thái ổn định mà đầu này sẽ là đầu ra của đầu kia. Chức năng của mạng gồm có 2 tầng tương tác. Giả sử có một vector khởi tạo X cung cấp cho đầu vào của lớp noron Y. Đầu vào sẽ được xử lý và chuyển đổi thành đầu ra của Y theo sau:
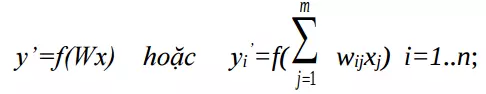 Đầu ra của lớp Y:
Đầu ra của lớp Y:
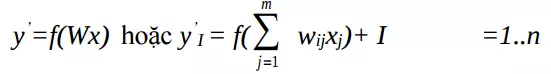 Đầu ra lớp X:
Đầu ra lớp X:
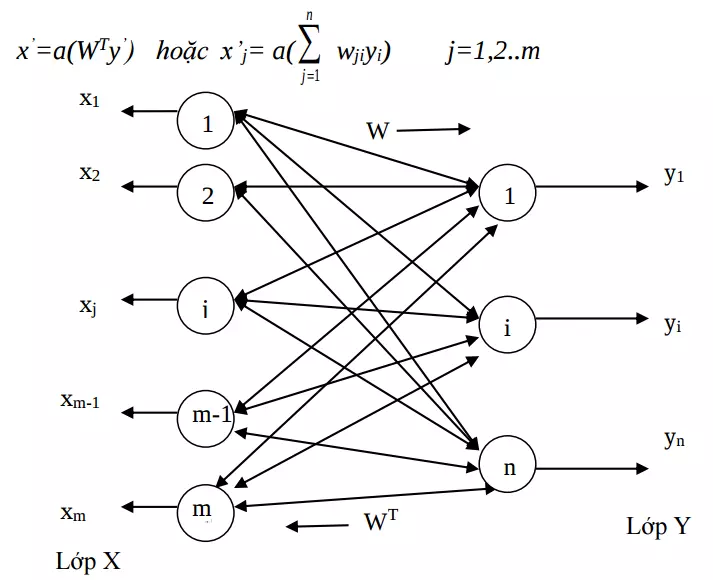 f (.) là hàm ngưỡng. Vector y’ cung cấp cho lớp X và vector x’ cung cấp đầu vào cho lớp Y cho đầu ra y’’.Quá trình sẽ tiếp tục cho tới khi cập nhật x và y dừng lại. Quá trình truy hồi đệ quy có thể gồm các bước sau:
f (.) là hàm ngưỡng. Vector y’ cung cấp cho lớp X và vector x’ cung cấp đầu vào cho lớp Y cho đầu ra y’’.Quá trình sẽ tiếp tục cho tới khi cập nhật x và y dừng lại. Quá trình truy hồi đệ quy có thể gồm các bước sau:
 Trạng thái cập nhật có thể là đồng bộ hoặc không đồng bộ.
Thuật toán lưu trữ
Với p cặp vector liên kết lưu trữ trong BAM:
Trạng thái cập nhật có thể là đồng bộ hoặc không đồng bộ.
Thuật toán lưu trữ
Với p cặp vector liên kết lưu trữ trong BAM:
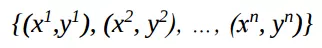 trong đó, //ảnh 52
trong đó, //ảnh 52
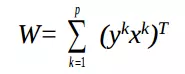 cho các vector lưỡng cực : {1, -1}
cho các vector lưỡng cực : {1, -1}
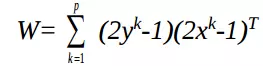 cho các vector nhị phân : {0, 1}
hoặc
cho các vector nhị phân : {0, 1}
hoặc
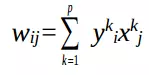 Cho các vector lưỡng cực :{1, -1}
Cho các vector lưỡng cực :{1, -1}
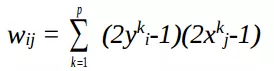 cho các vector nhị phân :{0, 1}
cho các vector nhị phân :{0, 1}
Tính ổn định của BAM (được chứng minh dùng định lý của Lyapunov)
Hàm năng lượng:
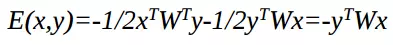 Xem xét ∆E sinh ra do ∆y ta có
Xem xét ∆E sinh ra do ∆y ta có
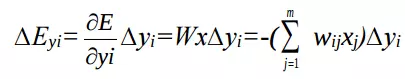 Có 3 trường hợp xảy ra:
Có 3 trường hợp xảy ra:
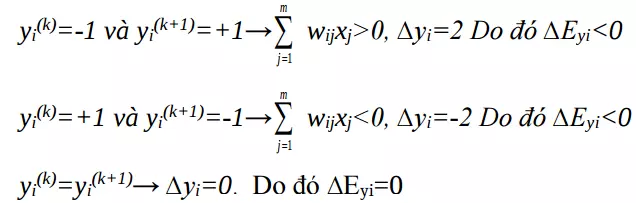 Đối với ∆x làm tương tự
Dung lượng bộ nhớ
Ước lượng p ≤ min(m,n) hoặc có thể xác định
Đối với ∆x làm tương tự
Dung lượng bộ nhớ
Ước lượng p ≤ min(m,n) hoặc có thể xác định 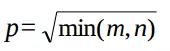
Ví dụ: Dùng mạng BAM để nhớ, nhận dạng - gán nhãn
Ví dụ này minh họa khả năng của mạng BAM dùng làm bộ nhớ liên kết địa chỉ hóa nội dung với khích thước m x n ; nhận mẫu đầu vào, gán nhãn đầu ra; khả năng chịu lỗi.
Bộ nhớ liên kết 2 chiều thường được dùng để minh hoạ việc cô lập lỗi và điều khiển. BAM là mạng phản hồi 2 lớp của các thành phần tương tác như là các bộ lưu trữ nhớ liên kết (Recall Stored Asociations) với (Xi, Yi) i=1...q. Như vậy, một vector x có n chiều đầu vào sẽ cho kết quả ra là vector y có m đầu ra. Mạng được xây dựng từ ma trận trọng cố định W kích cỡ m x n.
Quá trình xử lý phần tử tại bước thứ k tại lớp ra y được cập nhật như sau:
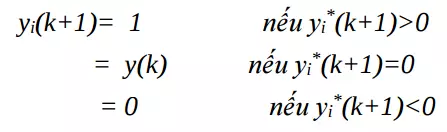 Cấu trúc lớp ra được mô tả
Cấu trúc lớp ra được mô tả
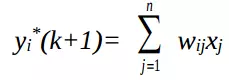 Quá trình xử lý phần tử tại bước thứ k tại lớp X được cập nhật như sau:
Quá trình xử lý phần tử tại bước thứ k tại lớp X được cập nhật như sau:
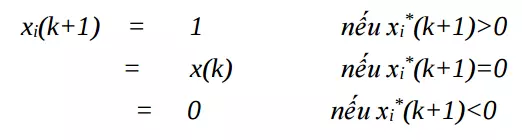 Cấu trúc lớp vào được mô tả
Cấu trúc lớp vào được mô tả 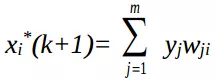 Việc cập có thể được thực hiện đồng bộ tức là tất cả các phần tử xử lý được cập nhật trong một chu trình đồng hồ, hoặc được thực hiện không đồng bộ khi chỉ có một tập con được cập nhật tại mỗi thời điểm.
Hàm năng lượng được xác định như công thức ở trên
Luật Hebb
Việc cập có thể được thực hiện đồng bộ tức là tất cả các phần tử xử lý được cập nhật trong một chu trình đồng hồ, hoặc được thực hiện không đồng bộ khi chỉ có một tập con được cập nhật tại mỗi thời điểm.
Hàm năng lượng được xác định như công thức ở trên
Luật Hebb 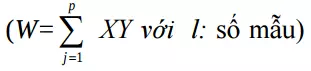 có thể đựơc dùng để mờ hóa q liên kết (Xi,Yi) trong BAM trong việc thể hiện vector dạng nhị phân (Binary Representation) thành dạng** lưỡng cực** (Bipolar Representation)
Như thay 0 thành -1.
Cho (Ai, Bi) là dạng lưỡng cực thì kết quả ma trận trọng số là:
có thể đựơc dùng để mờ hóa q liên kết (Xi,Yi) trong BAM trong việc thể hiện vector dạng nhị phân (Binary Representation) thành dạng** lưỡng cực** (Bipolar Representation)
Như thay 0 thành -1.
Cho (Ai, Bi) là dạng lưỡng cực thì kết quả ma trận trọng số là:
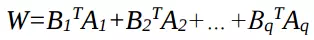 Vấn đề cho các bộ cảm ứng và bộ xác định cô lập lỗi (actuator failure isolation) trong việc quan tâm đến việc cải thiện bộ tin cậy của hệ thống điều khiển.
Sau đây là một BAM dùng như bộ ánh xạ liên kết từ không gian đặc trưng hệ thống sang không gian lỗi nhãn hệ thống.
Vấn đề cho các bộ cảm ứng và bộ xác định cô lập lỗi (actuator failure isolation) trong việc quan tâm đến việc cải thiện bộ tin cậy của hệ thống điều khiển.
Sau đây là một BAM dùng như bộ ánh xạ liên kết từ không gian đặc trưng hệ thống sang không gian lỗi nhãn hệ thống.
Xác định định được 3 lớp lỗi thông qua các vector chức năng và tương ứng với các vector nhóm.
Kết quả của sản phẩm đầu ra đưa đến ma trận trọng số
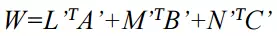 Giả sử có ba mẫu (k=3) cần nhớ được mã hoá từ trước ở dạng các giá trị đặc trưng là 1 hoặc 0 với năm phần tử nơ ron ra; 6 nơ ron đầu vào.
Giả sử có ba mẫu (k=3) cần nhớ được mã hoá từ trước ở dạng các giá trị đặc trưng là 1 hoặc 0 với năm phần tử nơ ron ra; 6 nơ ron đầu vào.
| Vector đặc trưng | Vector nhãn |
|---|---|
| A=(1 0 1 0 11), A'=(1-1 1-1 1 1) | L=(1 1 1 1 1), L'=(1 1 1 11) |
| B=(1 0 1 0 0 0), B'=(1-1 1-1-1-1) | M=(0 1 1 0 0), M'=(-1 1 1 -1-1) |
| C=(0 1 0 1 1 1), C'=(-1 1-1 1 1 1) | N=(1 0 0 1 1), N'=(1 -1 -1 11) |
Kết quả của sản phẩm đầu ra đưa đến ma trận trọng số
 Tương tự ta có:
Tương tự ta có:
 Sử dụng công thức, ví dụ trên có thể được xác định lại:
Sử dụng công thức, ví dụ trên có thể được xác định lại:
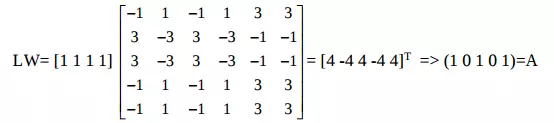 Như vậy (A, L), (B, M), (C < N) là các điểm cố định cho BAM bởi công thức và ma trận trọng W xác định nhờ công thức
Hơn nữa nếu cho vector (A+S) (thay đổi một chỳt vector A) vào BAM, thì nó vẫn hội tụ gần nhất tới lỗi nhóm L. Ví dụ
Như vậy (A, L), (B, M), (C < N) là các điểm cố định cho BAM bởi công thức và ma trận trọng W xác định nhờ công thức
Hơn nữa nếu cho vector (A+S) (thay đổi một chỳt vector A) vào BAM, thì nó vẫn hội tụ gần nhất tới lỗi nhóm L. Ví dụ
Chú ý rằng việc học với BAM là cố định, vì vậy nó không đủ mạnh trong trường hợp đẩy 1 bit trong 1 mẫu có thể kết quả hội tụ được là sai. BAM là ví dụ của mạng ánh xạ
4. Kết luận
Việc sử dụng các model trong training là vô cùng cần thiết, nhưng chúng ta cần tìm hiểu sâu hơn về việc làm như thế nào để có thể tạo ra được model đó để có thể sử dụng model một cách hợp lý và hiệu quả nhất để môt lúc nào đó model là do chính chúng ta tạo ra!
All rights reserved