2.2K 123 40

Đã đăng vào thg 6 30, 2017 3:09 CH 12 phút đọc

7.3K

Machine learning : K-means Clustering

Bài đăng này đã không được cập nhật trong 3 năm

Trong bài trước, chúng ta học thuật toán Hồi qui tuyến tính Linear Regression. Đây là thuật toán đơn giản nhất trong Supervised learning. Bài viết này chúng ta chuyển sang học về một thuật toán cơ bản trong Unsupervised learning - thuật toán K-means clustering (phân nhóm K-means). Đây là là một thuật toán khá gần gũi với tôi vì trong quá trình làm nghiên cứu ở đại học, tôi đã làm khá sâu về graph và đường đi ngắn nhất với bài toàn tìm k Nearest Neighbor.

Hiểu về K-Means Clustering

Trước hết chúng ta sẽ tìm hiểu về thuật toán K-means clustering trước bằng ví dụ :

Bài toán kích thước áo T-shirt

Giả sử có một công ty định ra mắt một mẫu sản phẩn mới T-shirt vào thị trường. Tất nhiên họ sẽ phải sản xuất rất nhiều size để phù hợp với sự đa dạng của thị trường người dùng. Với định hướng đo, công ty đã tiến hành khảo sát dữ liệu chiều cao và cân nặng của người dùng, và vẽ nó thành 1 đồ thị như sau :

alt

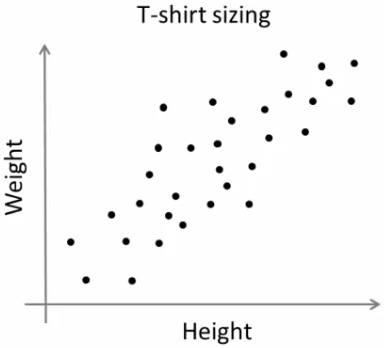
Công ty này ko thể đủ nguồn lực để có thể sản xuất áo với tất cả mọi size. Thực tế này trong kinh doanh bạn cũng dễ dàng hiểu được. THay vì đó, họ sẽ chia số lượng người dùng thành các size như là Small, Medium, Large và sản xuất chỉ 3 mẫu như thế. 3 mẫu này là đủ khớp với tất cả mọi người và thị trường. Ở đây việc phân chia các người dùng vào 3 nhóm trên sẽ được xử lý bằng kĩ thuật phân nhóm K-means. Thuật toán này sẽ cho ta 3 size áo tối ưu nhất - thoã mãn tất cả mọi người. Tất nhiên, nếu như ko thể tìm được 3 size áo vừa vặn thoả mãn mọi người trong nhóm, công ty sẽ chia nhỏ nhóm thêm thành nhiều nhóm khác, có thể là 5, có thể là nhiều hơn nữa .... Bạn nhìn hình sẽ rõ nhé

alt

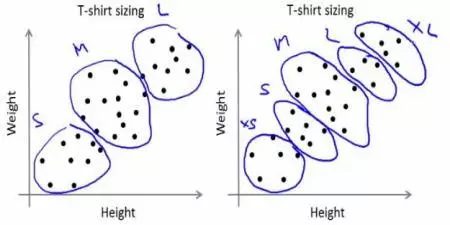
Làm thế nào mà chia nhỏ được thế

Thuật toán này sẽ là một vòng lặp. Để đơn giản mình sẽ mô tả từng step của thuật toán và môt chút hình minh hoạ.

Hãy xem nhóm dữ liệu như đồ thị dưới ( để dễ hình dung thì bạn hãy xem đây như là đồ thị về chiều cao - cân nặng của nhóm người dùng ). Chúng ta sẽ nhóm các dữ liệu thành 2 nhóm.

alt

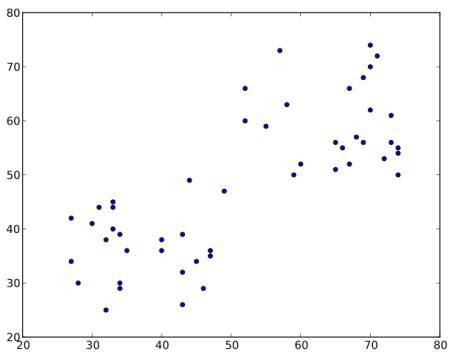
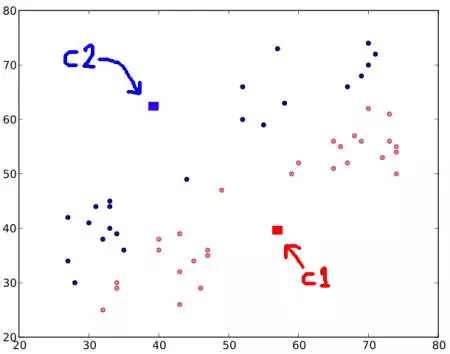
STEP 1 : Thuật toán này chọn ngẫu nhiên 2 trọng tâm. C1 và C2 ( thỉnh thoảng, bất kì 2 cặp điểm nào cũng sẽ được xem như là 2 cặp trọng tâm ).

STEP 2 : Tính toán khoảng cách từ mỗi điểm đến 2 trọng tâm đó. Nếu một dữ liệu thử nghiệm là gần với C1 hơn thì nó sẽ được gán nhãn '0'. Nếu đó là gần với C2 hơn, nó sẽ được dán nhãn là '1' (nếu bạn dùng nhiều trọng tâm hơn thì bạn sẽ có nhiều label hơn ví dụ như '2', '3' v.v... ).

Trong hình, chúng ta sẽ tô màu cho các nhãn 0 là đỏ và xanh cho các nhãn 1. Chúng ta có hình như dưới :

alt

STEP 3 : Tiếp theo chúng ta tính toán trung bình của tất cả các điểm màu xanh và đỏ riêng biệt. Kết quả này sẽ cho phép quyết định được trọng tâm mới. C1 và C2 sẽ được tái thiết lập vị trí mới với các điểm dữ liệu mới ( chú ý, các hình ảnh dưới ko phải là giá trị thật đây chỉ là ví dụ thôi nhé ).

Tiếp, chúng ta lại lặp lại bước 2. Chúng ta có kết quả như sau :

alt

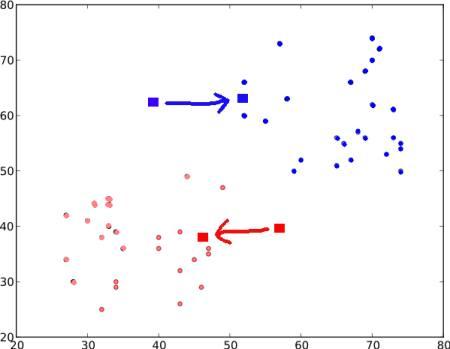
Bây giờ, bước 2 và bước 2 sẽ được lặp đi lặp lại cho đến khi trọng tâm được hội tụ về 1 điểm cố định. Hoặc đơn giản là nó sẽ dừng lại ở trong một phạm vi - thoả mãn một chuẩn mà chúng ta đã đưa ra từ trước. Ví du như là đạt đến số lần vòng lặp tối đa đã định nghĩa trước, hoặc là đạt được một chuẩn chính xác nào đó .v... Các điểm này sẽ thoả mãn tổng khoảng cách giữa dữ liệu test và trọng tâm tương ứng là nhỏ nhất. Hoặc cũng có thể là tổng khoảng cách giữa C1 tới điểm đỏ và C2 tới điểm xanh là nhỏ nhất.

alt

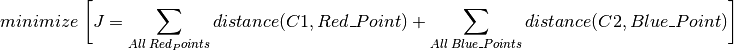
Cuối cùng chúng ta có trọng tâm như sau :

alt

K-Means Clustering sử dụng trong OpenCV

Mục tiêu của phần nay là sẽ giúp bạn sử dụng công cụ OpenCV - cụ thể là cv2.kmeans() để thực hiện thuật toán k-means.

Tìm hiểu về Parameters

samples : Mẫu thì nên là kiểu dữ liệu của np.float32, và mỗi đối tượng cần được đặt trọng một cột duy nhất.
nclusters (K): Số nhóm yêu cầu tại thời điểm cuối cùng
criteria : Đây là tiêu chí chấm dứt vòng lặp. Khi tiêu chí này được thỏa mãn, thuật toán sẽ dừng vòng lặp. Trên thực tế, nó phải là một nhóm 3 thông số (type, max_iter, epsilon):

3.a - loại tiêu chí chấm dứt: Nó có 3 lá cờ như sau: cv2.TERM_CRITERIA_EPS - ngăn sự lặp lại thuật toán nếu đạt được độ chính xác nhất định - epsilon đạt được. cv2.TERM_CRITERIA_MAX_ITER - dừng thuật toán sau khi số lượng nhất định được lặp đi lặp lại cv2.TERM_CRITERIA_EPS max_iter + cv2.TERM_CRITERIA_MAX_ITER - ngăn chặn sự lặp đi lặp lại khi một trong các điều kiện trên nó được đáp ứng
3.b - max_iter - Một số nguyên xác định số lượng tối đa vòng lặp.
3.c - Độ chính xác - epsilon

attempts: Cờ để xác định số lần các thuật toán được thực hiện bằng cách sử dụng việc đánh nhãn khởi tạo khác nhau.
flags : Cờ này được sử dụng để xác định trung tầm ban đầu được chọn như thế nào. Về cơ bản có 2 cờ được sử dụng là : cv2.KMEANS_PP_CENTERS và cv2.KMEANS_RANDOM_CENTERS.

Output parameters

compactness : Đây là tổng của bình phương khoảng cách từ mỗi điểm đến trọng tâm tương tự của họ.
labels : Đây là mảng các label trong đó mỗi phần tử của mảng được đánh dấu '0', '1' .....
centers : Đây là mảng trọng tâm của các nhóm.

Bây giờ chúng ta sẽ thấy làm thế nào để áp dụng thuật toán K-Means với ví dụ.

Dữ liệu với chỉ một biến

Hãy xem xét, bạn có một bộ dữ liệu chỉ với một tính năng, tức là một chiều. Ví dụ như bài toán áo T-shirt ở trên nhưng chúng ta chỉ sử dụng mỗi chiều cao của người dùng để quyết định size áo .

Chúng ta sẽ bắt đầu bằng cách tạo ra dữ liệu và vẽ nó trên đồ thị trong Matplotlib :

import numpy as np
import cv2
from matplotlib import pyplot as plt

x = np.random.randint(25,100,25)
y = np.random.randint(175,255,25)
z = np.hstack((x,y))
z = z.reshape((50,1))
z = np.float32(z)
plt.hist(z,256,[0,256]),plt.show()

Chúng ta có z là một mảng có kích thước 50, và các giá trị khác nhau từ 0 đến 255. Cho z thành một vector cột. Sau đó, chúng ta tạo dữ liệu của loại np.float32.

Chúng ta sẽ có hình ảnh sau:

alt

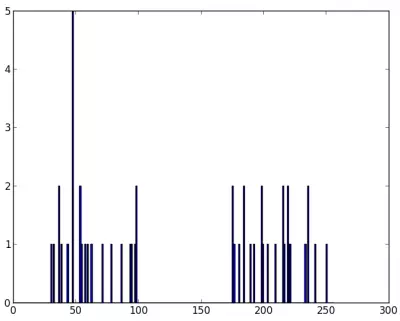
Bây giờ chúng ta áp dụng thuật toán K-Means. Trước đó chúng ta cần xác định các tiêu chí. Tiêu chuẩn của tôi là, bất cứ khi nào 10 lần lặp của thuật toán được chạy, hoặc đạt được độ chính xác của epsilon = 1.0, thuật toán sẽ dừng và trả về kết quả :

# Define criteria = ( type, max_iter = 10 , epsilon = 1.0 )
criteria = (cv2.TERM_CRITERIA_EPS + cv2.TERM_CRITERIA_MAX_ITER, 10, 1.0)

# Set flags (Just to avoid line break in the code)
flags = cv2.KMEANS_RANDOM_CENTERS

# Apply KMeans
compactness,labels,centers = cv2.kmeans(z,2,None,criteria,10,flags)

Việc này sẽ cho ta các giá trị về compactness, label và trọng tâm. Trong trường hợp này, ta có các trung tâm là 60 và 207. Nhãn sẽ có cùng kích thước với dữ liệu test, ở đây mỗi dữ liệu sẽ được gắn nhãn là '0', '1', '2' v.v... tùy thuộc vào trọng tâm của chúng. Bây giờ ta chia dữ liệu vào các nhóm khác nhau tùy thuộc vào nhãn của chúng.

A = z[labels==0]
B = z[labels==1]

Bây giờ chúng ta sẽ vẽ A màu đỏ và B màu xanh và trọng tâm của chúng bằng màu vàng.

# Now plot 'A' in red, 'B' in blue, 'centers' in yellow
plt.hist(A,256,[0,256],color = 'r')
plt.hist(B,256,[0,256],color = 'b')
plt.hist(centers,32,[0,256],color = 'y')
plt.show()

Chúng ta sẽ có kết quả như sau :

alt

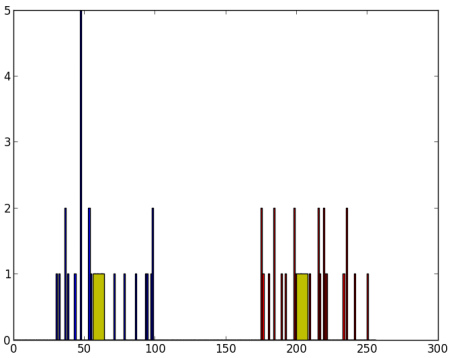
Dữ liệu với chỉ nhiều biến

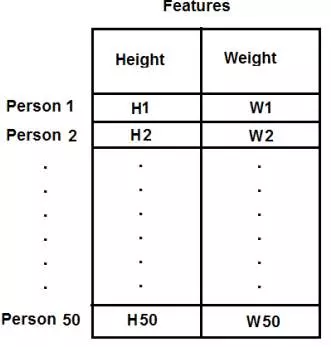
Trong ví dụ ở trên, chúng ta chỉ có chiều cao để quyêt định bài toán. Bây giơ, hãy cân nhắc luôn cả cân nặng nhé . Bài toán sẽ trở thành phân nhóm tập các chiều cao - cân nặng. Chú ý rằng ở ví dụ trước, chúng ta lưu dữ liệu vào một vector đơn. Mỗi biến sẽ được sắp xếp trong một cột, mỗi cột sẽ tương ứng với một giá trị test được đẩy vào. Trong trường hợp này, giả sử chúng ta có tập dữ liệu 50x2, tức là sẽ có cặp chiều cao - cân nặng của 50 người. Cột đầu tiên sẽ tương ứng với chiều cao của 50 người và cột thứ 2 là cân nặng của họ. Dòng dầu tiên tương ứng với 2 yếu tố ( chiều cao - cân nặng ) của người thứ nhất. v.v... tương tự như vậy cho đến dòng số 50.

Giải thích có vẻ hơi dài dòng nhưng nếu bạn nào còn nhớ kiến thức toán về ma trận hẳn sẽ định hình được ngay ý niệm này trong đầu :

alt

Tiếp, chúng ta sẽ code như sau :

import numpy as np
import cv2
from matplotlib import pyplot as plt

X = np.random.randint(25,50,(25,2))
Y = np.random.randint(60,85,(25,2))
Z = np.vstack((X,Y))

# convert to np.float32
Z = np.float32(Z)

# define criteria and apply kmeans()
criteria = (cv2.TERM_CRITERIA_EPS + cv2.TERM_CRITERIA_MAX_ITER, 10, 1.0)
ret,label,center=cv2.kmeans(Z,2,None,criteria,10,cv2.KMEANS_RANDOM_CENTERS)

# Now separate the data, Note the flatten()
A = Z[label.ravel()==0]
B = Z[label.ravel()==1]

# Plot the data
plt.scatter(A[:,0],A[:,1])
plt.scatter(B[:,0],B[:,1],c = 'r')
plt.scatter(center[:,0],center[:,1],s = 80,c = 'y', marker = 's')
plt.xlabel('Height'),plt.ylabel('Weight')
plt.show()

Kết quả chúng ta có được :

alt

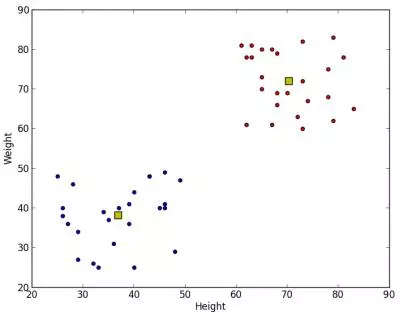
Color Quantization

Color Quantization là một process giảm số lượng màu trong một hình ảnh.

Lý do để giảm chất lượng ảnh là để giảm thiểu dung lượng nhớ và tải server or đơn giản là đôi khi trên một số thiết bị có thể có giới hạn sao cho nó có thể sản xuất chỉ số lượng màu giới hạn. Trong những trường hợp đó, lượng tử hóa màu được thực hiện. Ở đây chúng ta sử dụng k-means clustering để "trung bình hoá màu".

Hẳn là bạn đã nhận ra sự liên quan rồi nhỉ. Màu sẽ có 3 biến là R, G, B. Vì vậy, chúng ta cần định hình lại image vào một mảng có kích thước Mx3 (M là số pixel trong images). Sau khi phân nhóm, chúng ta thay giá trị trọng tâm ( R, G, B ) cho tất cả các điểm ảnh sao cho hình ảnh mới sẽ chỉ có một số lượng màu xác định. Tiếp tục, chúng ta lại reshape nó trở lại dạng hình ảnh bình thường :

Code sẽ như sau :

import numpy as np
import cv2

img = cv2.imread('home.jpg')
Z = img.reshape((-1,3))

# convert to np.float32
Z = np.float32(Z)

# define criteria, number of clusters(K) and apply kmeans()
criteria = (cv2.TERM_CRITERIA_EPS + cv2.TERM_CRITERIA_MAX_ITER, 10, 1.0)
K = 8
ret,label,center=cv2.kmeans(Z,K,None,criteria,10,cv2.KMEANS_RANDOM_CENTERS)

# Now convert back into uint8, and make original image
center = np.uint8(center)
res = center[label.flatten()]
res2 = res.reshape((img.shape))

cv2.imshow('res2',res2)
cv2.waitKey(0)
cv2.destroyAllWindows()

Kết quả với K = 8 :

alt