8.8K 668 107

Đã đăng vào thg 6 10, 2022 6:04 SA 5 phút đọc

24.2K

Bài 8: Sử dụng mảng làm tham số của hàm

I. Truyền mảng một chiều

Mảng cũng có thể được truyền vào hàm giống như một tham số để tính toán. Có $3$ cách để truyền mảng vào hàm: Sử dụng tham số mảng có kích cỡ, sử dụng tham số mảng không có kích cỡ và sử dụng con trỏ. Trong bài học này chúng ta sẽ tập trung vào hai cách đầu tiên, còn cách thứ ba với C++ là không cần thiết nên sẽ không đề cập ở đây.

Cú pháp:

Truyền mảng có kích cỡ:

{Kiểu_trả_về} {Tên_hàm}({Kiểu_phần_tử} {Tên_mảng}[{Kích_cỡ}])

Ví dụ:

int function1(int a[10])
{
    {Thân_hàm};
}

Truyền mảng không kích cỡ:

{Kiểu_trả_về} {Tên_hàm}({Kiểu_phần_tử} {Tên_mảng}[])

Ví dụ:

int function2(int a[])
{
    {Thân_hàm};
}

Khác với việc truyền biến vào hàm, việc truyền mảng vào hàm không phân biệt ra tham trị hay tham chiếu. Khi truyền mảng, hệ thống luôn luôn truyền trực tiếp địa chỉ của phần tử đầu tiên của mảng ban đầu vào hàm, dẫn đến mọi thay đổi trên tham số đại diện trong hàm sẽ tác động đến mảng gốc bên ngoài, dù là theo cách nào trong số các cách trên. Vì vậy cần hết sức chú ý đến dữ liệu khi thực hiện truyền mảng vào hàm. Dưới đây là ví dụ cụ thể:

#include <bits/stdc++.h>

using namespace std;

void increase(int b[])
{
    for (int i = 0; i <= 4; ++i)
        ++b[i];
}
	
int main()
{
    int a[5] = {1, 2, 3, 4, 5};
    increase(a);

    cout << "Mảng sau khi tăng lên: ";
    for (int i = 0; i <= 4; ++i)
	cout << a[i] << ' ';
		
    return 0;
}

Khi biên dịch và chạy chương trình này, ta sẽ thu được kết quả:

Mảng sau khi tăng lên: 2 3 4 5 6

Trong phần tham số của hàm void increase(int b[]), nếu ta thay int b[] bằng int b[5] thì cũng vẫn trả ra kết quả tương tự, do hệ thống sẽ không tạo ra một bản sao của mảng mà lấy trực tiếp địa chỉ của mảng gốc rồi truyền vào hàm.

Một lưu ý khác là C++ không cho phép trả về trực tiếp một mảng như là kết quả của hàm. Để trả ra kết quả cho hàm là một mảng, cần phải sử dụng con trỏ, nhưng việc đó khá phức tạp. Để tránh việc phải trả ra kết quả là một mảng, ta nên khai báo các mảng là biến toàn cục hoặc sử dụng kiểu mảng động <vector> (sẽ học ở bài số $9$ ).

II. Truyền mảng hai chiều

Về bản chất, mảng hai chiều thực ra là một "mảng chứa các mảng", nghĩa là nó giống như một mảng một chiều nhưng mỗi phần tử lại là một mảng một chiều khác. Do đó, trên bộ nhớ, toàn bộ các phần tử của mảng hai chiều thực ra được viết liền kề với nhau, chứ không phải tạo thành một bảng số như chúng ta vẫn tưởng tượng.

Chính vì thế, khi truyền mảng hai chiều vào hàm thì thực chất chương trình vẫn sẽ truyền địa chỉ của phần tử đầu tiên trong mảng hai chiều vào hàm. Chẳng hạn, với một mảng hai chiều $3 \times 3$ thì địa chỉ của các phần tử trên thanh RAM sẽ trông như thế này:

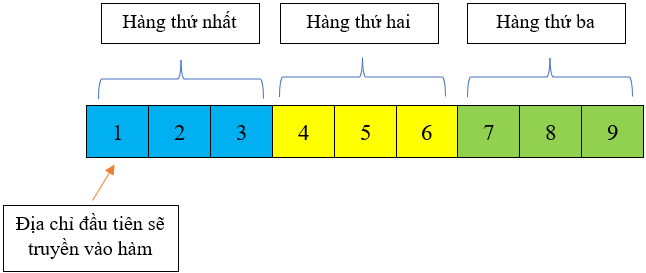
Mảng hai chiều cũng có thể được truyền vào hàm như mảng một chiều, tuy nhiên có một số lưu ý khi khai báo tham số hình thức. Có ba cách để truyền mảng hai chiều vào hàm:

Cách

1

: Khai báo cụ thể số hàng, số cột:

{Kiểu_trả_về} {Tên_hàm}({Kiểu_phần_tử} {Tên_mảng}[{Số_hàng}][{Số_cột}])

Cách

2

: Khai báo cụ thể số cột, số hàng bỏ trống:

{Kiểu_trả_về} {Tên_hàm}({Kiểu_phần_tử} {Tên_mảng}[][{Số_cột}])

Cách

3

: Sử dụng từ khóa typedef để định nghĩa trước kiểu mảng:

typedef {Kiểu_dữ_liệu} {Tên_thay_thế}[{Số_hàng}][{Số_cột}];

// Khi truyền vào hàm.
{Kiểu_trả_về} {Tên_hàm}({Tên_thay_thế} {Tên_mảng});

Ví dụ, nếu truyền mảng $3 \times 3$ vào hàm void function() thì ta có thể khai báo tham số hình thức theo các cách sau đều được:

typedef int arr[100][100];

void function(int a[3][3]); // Cách 1.
void function(int a[][3]); // Cách 2.
void function(arr a); // Cách 3.

Thông thường, cách thứ $2$ và $3$ sẽ được ưu tiên sử dụng hơn. Lưu ý nhỏ, nếu các bạn truyền mảng từ hai chiều trở lên thì chỉ có chiều đầu tiên được phép để trống kích thước, còn các chiều sau đó đều phải xác định kích thước. Ví dụ, cách khai báo tham số int a[][] sẽ là không hợp lệ và bị báo lỗi khi biên dịch.

III. Tài liệu tham khảo

I. Truyền mảng một chiều

II. Truyền mảng hai chiều

III. Tài liệu tham khảo

Mục lục