Làm việc với đường cong Bezier trong Unity
Bài đăng này đã không được cập nhật trong 4 năm
Xin chào mọi người, hôm nay mình xin giới thiệu một kỹ thuật trong Unity đó là đường cong Bezier và cách sử dụng kỹ thuật này trong Unity.
Mục đích của bài viết
Cung cấp cho mọi người thông tin cơ bản về đường cong Bezier và ứng dụng nó trong game.
Giới thiệu
Đường cong Bezier là một trong những đường cong cơ bản nhất, thường được sử dụng trong đồ họa máy tính và xử lý hình ảnh. Đường cong Bezier có thể được sử dụng để tạo ra những con đường, dòng sông hoặc các loại đường cong khác trong game của bạn. Đường cong Bezier được công bố lần đầu vào năm 1962 bởi một kĩ sư người Pháp Pierre Bézier nên được gọi là đường cong Bezier.
Một đường cong Bezier được định nghĩa bởi một tập hợp các điểm control từ P0 đến Pn trong đó n được gọi là thứ tự của nó.(n=1 là đường cong tuyến tính hay còn gọi là đường cong bậc một, n=2 là đường cong bậc hai). Điểm đầu và điểm cuối của đường cong Bezier luôn luôn là những điểm cuối của đường cong và các điểm trung gian của đường cong sẽ thường không nằm trên đường cong này.
Linear Interpolation (Nội suy tuyến tính)
Linear interpolation (nội suy tuyến tính) giữa hai điểm đã biết trước nghĩa là tìm ra những điểm ở giữa hai điểm đã cho dựa vào các giá trị t khác nhau. Trong đó 0 <= t <= 1, nếu mọi người đã sử dụng Mathf.Lerp hoặc Vector3.Lerp sẽ rất quen thuộc với khái niệm này. Chúng ta hãy đến với công thức để tìm điểm nội suy P giữa điểm P0 và P1 như sau:
P = P0 + t( P1 - P0 ), với 0 <= t <= 1
Dựa vào công thức này ta có thể lấy ra điểm nội suy bằng cách nhân t với khoảng cách giữa hai điểm P1 và P0 cộng với điểm đầu là P0. Như vậy ta có:
khi t=0, P = P0.
khi t=1, P = P1.
khi t=0.5, P sẽ ở giữa hai điểm P0 và P1.
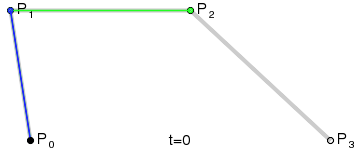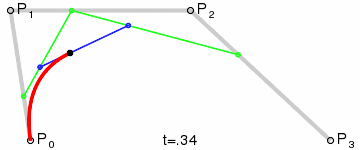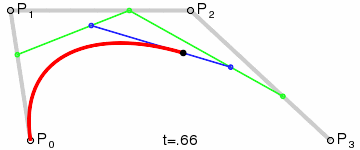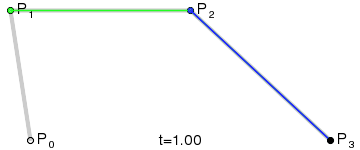
Đường cong Bezier tuyến tính
Đường cong Bezier tuyến tính có hai điểm control. Từ hai điểm P(0) và P(1), ta sẽ có một đường cong Bezier tuyến tính là một đường thẳng giữa hai điểm đó. Công thức tính điểm nội suy trong trường hợp này như sau:
P = P0 + t(P1-P0) = (1 - t)P0 + tP1, với 0 <= t <= 1
Mô tả chuyển động của đối tượng trên một đường cong Bezier tuyến tính được thể hiện ở ảnh bên dưới:
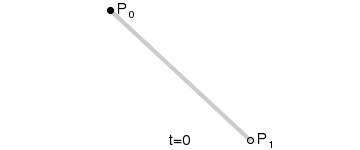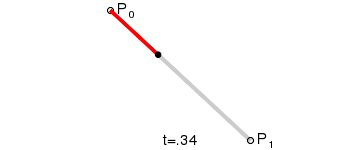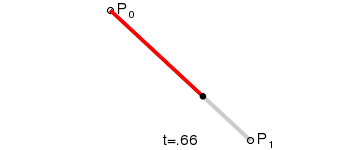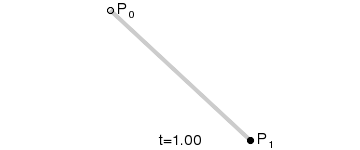
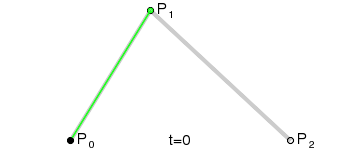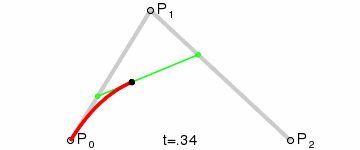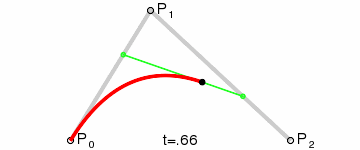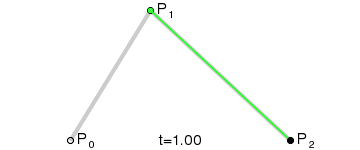
Đường cong Bezier bậc hai
Đường cong Bezier bậc hai có 3 điểm control. Đường cong Bezier là một đường có các điểm nội suy được tính từ hai đường Bezier tuyến tính. Từ ba điểm P0, P1, P3 cho trước, ta sẽ có đường cong Bezier là phép tính nội suy tuyến tính từ hai điểm được lấy từ đường Bezier tuyến tính giữa P0 và P1 và đường Bezier tuyến tính giữa P1, và P2. Công thức để tính đường cong Bezier bậc hai như sau:

Trong đó B(P0,P1) là điểm nội suy giữa hai điểm P0 và P1 và B(P1,P2) là điểm nội suy giữa P1 và P2, thay công thức nội suy tuyến tính ta sẽ được công thức:

rút gọn lại ta được công thức hoàn chỉnh như sau:

chuyển động của vật thể trên đường cong Bezier bậc hai được thể hiện như sau:
Đường cong Bezier bậc ba(Cubic)
Đường cong Bezier bậc ba có bốn điểm control và là tập hợp các điểm nội suy được tính từ hai đường cong bezier bậc hai. Từ bốn điểm P0, P1, P2 và P3, 1 đường cong bezier bậc ba là phép nội suy tuyến tính của hai điểm, được lấy từ đường cong Bezier bậc hai của ba điểm P0, P1 và P2, và đường cong Bezier bậc hai của ba điểm P1, P2 và P3. Công thứ của đường cong Bezier bậc ba như sau:

áp dụng công thức của hai đường Bezier bậc hai, ta có:

rút gọn lại ta được công thức:

Chuyển động của vật thể trên đường cong Bezier bậc ba được thể hiện như sau:
Như vậy, đường cong Bezier bậc n có thể được định nghĩa bằng một phép nội suy tuyến tính từ điểm đến điểm của hai điểm được tính từ hai đường cong bezier tương ứng cấp n-1.
Demo
Trong hầu hết các ứng dụng, chúng ta thường sử dụng đường cong Bezier bậc hai hoặc bậc ba, việc sử dụng các đường cong Bezier bậc cao hơn thường rất phức tạp và làm tăng quá trình tính toán nên thay vi sử dụng đương cong Bezier bậc cao chúng ta sẽ sử dụng đường cong bậc hai hoặc bậc ba nhiều lần. Dưới đây là một ví dụ về cách sử dụng đường cong Bezier để hiển thị dấu vô cực.
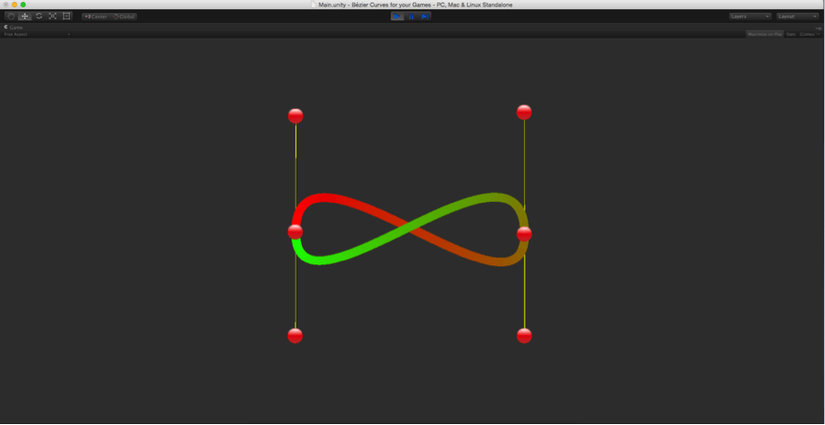
Để tạo được đường cong như trên thì chúng ta cần setup scene như sau:
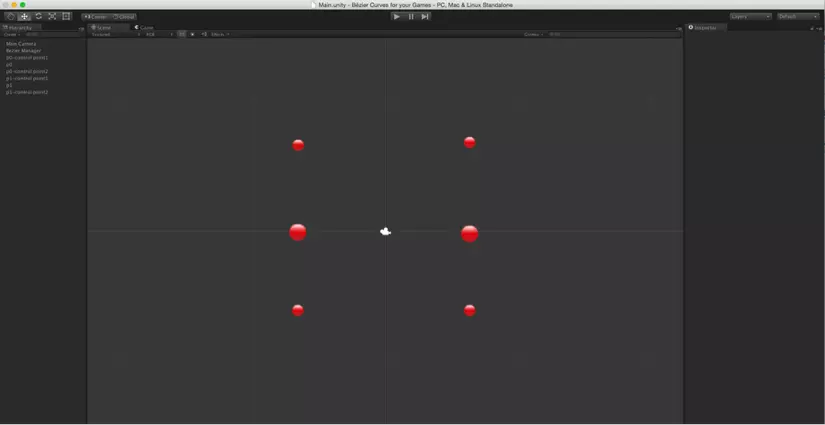
sau đó, chúng ta cần add script Bezier.cs vào đối tượng Bezier Manager. Bezier.cs:
using UnityEngine;
using System.Collections.Generic;
[RequireComponent(typeof(LineRenderer))]
public class Bezier : MonoBehaviour
{
public Transform[] controlPoints;
public LineRenderer lineRenderer;
private int curveCount = 0;
private int layerOrder = 0;
private int SEGMENT_COUNT = 50;
void Start()
{
if (!lineRenderer)
{
lineRenderer = GetComponent<LineRenderer>();
}
lineRenderer.sortingLayerID = layerOrder;
curveCount = (int)controlPoints.Length / 3;
}
void Update()
{
DrawCurve();
}
void DrawCurve()
{
for (int j = 0; j <curveCount; j++)
{
for (int i = 1; i <= SEGMENT_COUNT; i++)
{
float t = i / (float)SEGMENT_COUNT;
int nodeIndex = j * 3;
Vector3 pixel = CalculateCubicBezierPoint(t, controlPoints [nodeIndex].position, controlPoints [nodeIndex + 1].position, controlPoints [nodeIndex + 2].position, controlPoints [nodeIndex + 3].position);
lineRenderer.SetVertexCount(((j * SEGMENT_COUNT) + i));
lineRenderer.SetPosition((j * SEGMENT_COUNT) + (i - 1), pixel);
}
}
}
Vector3 CalculateCubicBezierPoint(float t, Vector3 p0, Vector3 p1, Vector3 p2, Vector3 p3)
{
float u = 1 - t;
float tt = t * t;
float uu = u * u;
float uuu = uu * u;
float ttt = tt * t;
Vector3 p = uuu * p0;
p += 3 * uu * t * p1;
p += 3 * u * tt * p2;
p += ttt * p3;
return p;
}
}
Ở đây, hàm CalculateCubicBezierPoint là hàm tính toán đường cong Bezier, hàm DrawCurve dùng để vẽ ra đường cong Bezier sử dụng line renderer. Bạn có thể thay đổi đường cong bằng cách thay đổi các điểm control như sau:
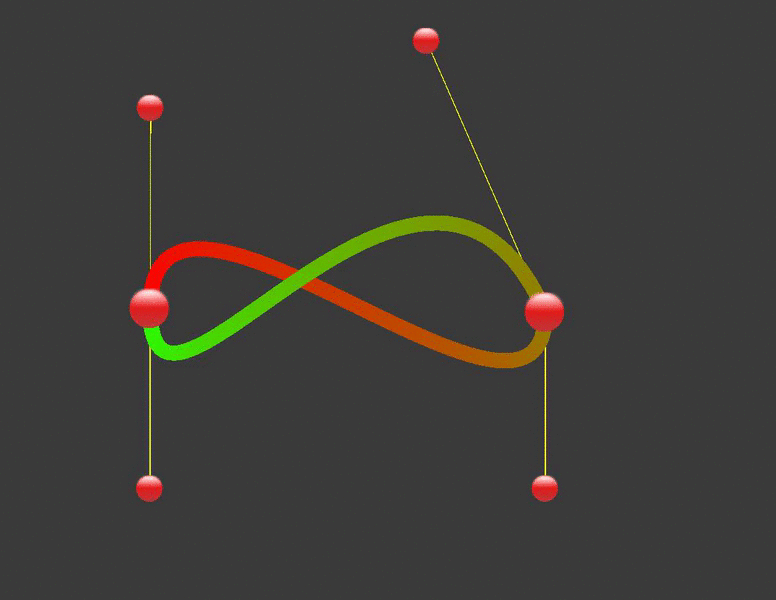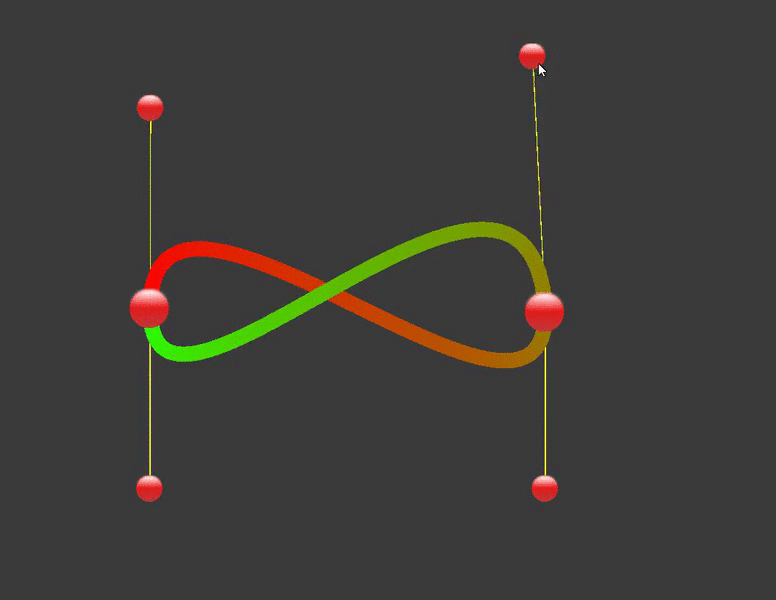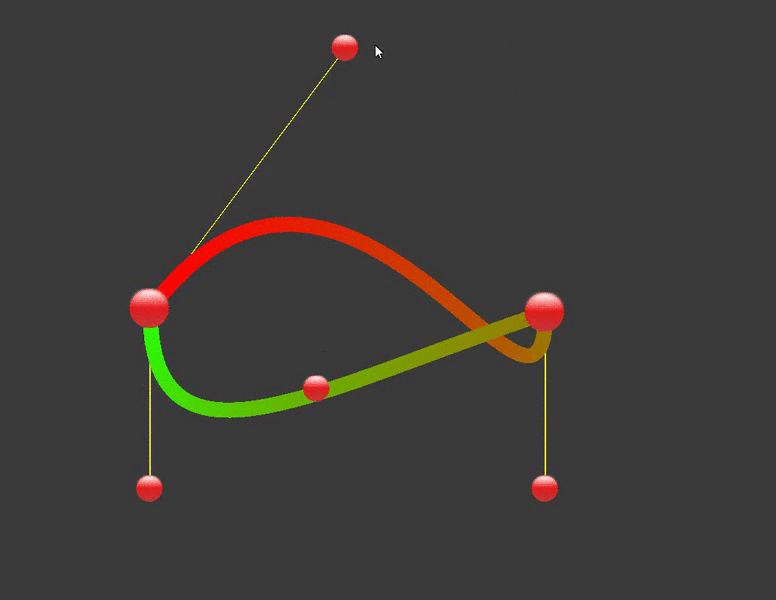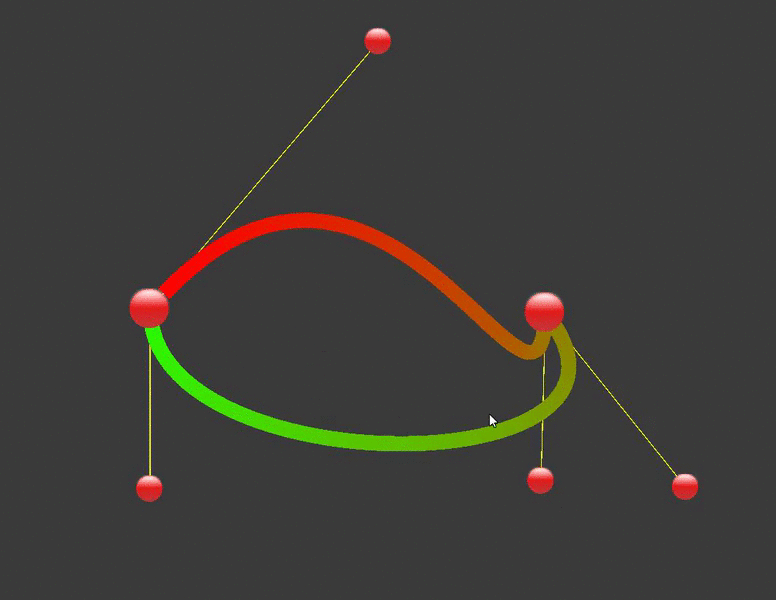
Kết luận
sau khi đọc đến đây, mình nghĩ rằng mọi người có thể đã nhận ra rằng chúng ta đã gặp đường cong Bezier trong rất nhiều ứng dụng nổi tiếng như Pen trong photoshop hay chỉnh sửa giá trị animation trong Unity, nó cho phép chúng ta dễ dàng điểu chỉnh đường cong. Hi vọng sau bài viết này mọi người có thể ứng dụng đường cong Bezier vào game của mình để tạo level hoặc map.
Bài viết này được dịch và tham khảo từ bài viết: http://www.theappguruz.com/blog/bezier-curve-in-games.
All rights reserved