Làm gì khi mô hình học máy thiếu dữ liệu có nhãn - Phần 2 - Semi Supervised Learning
Bài đăng này đã không được cập nhật trong 3 năm
Xin chào các bạn, tiếp nối bài viết trước về Active Learning - một trong những phương pháp hữu hiệu để xử lý đối với trường hợp thiếu dữ liệu có nhãn. Bài viết này mình xin phép được chia sẻ với các bạn một phương pháp khác đó là semi-supervised learning hay còn gọi với cái tên khác là học bán giám sát. Và không còn chần chừ gì nữa chúng ta sẽ bắt đầu ngay thôi. Gét gô.
Semi supervised learning là gì
Semi-supervsied learning là một phương pháp sử dụng kết hợp cả dữ liệu có nhãn và dữ liệu không nhãn trong quá trình huấn luyện mô hình học máy.
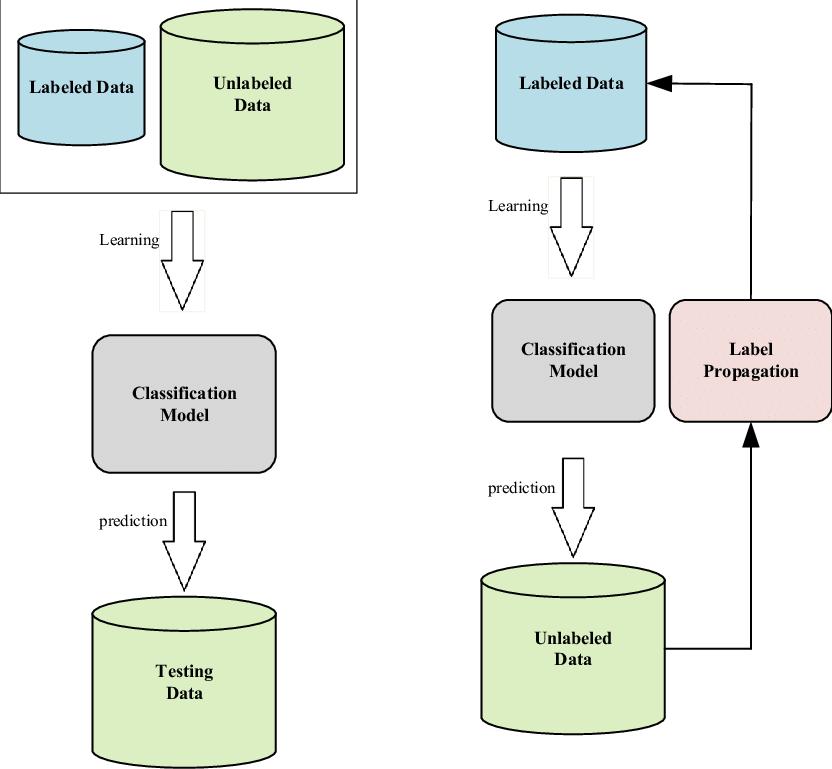
Các bạn có thể đặt câu hỏi rằng việc huấn luyện như vậy có sự khác biệt gì không? Ồ, chắc chắn là có rồi và chúng ta sẽ cùng nhau đi sâu tìm hiểu trong bài viết này. Xuyên suốt bài viết này, khái niệm loss function được hiểu là sự kết hợp giữa supervised loss và unsupervised loss . Supervsied loss không có gì xa lạ đối với các bạn nữa rồi vì dữ liệu là dữ liệu có nhãn. Chúng ta sẽ tìm hiểu rõ hơn về các thiết kế unsupervised loss . Chúng ta có thể để ý thấy một hàm là một ramp function giúp tăng mức độ quan trọng của unsupervised loss theo thời gian.
Các kí hiệu sử dụng trong bài
Để thuận tiện cho việc mô tả các thuật toán trong bài viết này, chúng ta sẽ cùng nhau dịnh nghĩa một số kí hiệu cần thiết. Đừng quá lo lắng nếu như bạn không phải là người thích các kí hiệu toán, mọi thứ mình sẽ cố gắng giải thích một cách dễ hiểu nhất các bạn nhé. Sau đây là bảng kí hiệu
| Kí hiệu | Ý nghĩa |
|---|---|
| Số lượng của các unique labels trong bài toán | |
| Tập dữ liệu có nhãn, y là biểu diễn one-hot của true label | |
| Tập dữ liệu không nhãn | |
| Toàn bộ tập dữ liệu bao gồm tập có nhãn và không có nhãn | |
| Bất kể sample nào trong tập dữ liệu (kể cả có nhãn hoặc không nhãn) | |
| Sample được apply augmentation | |
| Sample thứ | |
| Loss, supervised loss, unsupervised loss | |
| loss weight của dữ liệu không nhãn, là một hàm tăng theo thời gian | |
| Xác suất có điều kiện của label set khi biết đầu vào |
||Mạng nơ ron cần huấn luyện với tham số | ||Vector logits đầu ra của mạng nơn ron | ||The predicted label distribution.| ||Hàm đo khoảng cách giữa hai phân phối, có thể là MSE, cross entropy, KL divergence, etc.| ||Tham số weight EMA để cập nhật mô hình teacher - momentum| ||Các tham số cho thuật toán Mixup | ||Temperature for sharpening the predicted distribution.| ||Ngưỡng để lựa chọn độ tin cậy của nhãn giả. |
Một vài giả thuyết cần chú ý
Chúng ta có một vài giả thuyết chúng ta cần chú ý khi thiết kế một phương pháp semi-supervised learning như sau:
- H1 - Smoothness Assumptions: Giả thiết này nói rằng nếu như hai mẫu dữ liệu gần nhau trong các high-density regiion trong feature space thì nhãn của chúng cũng rất có khả năng tương đồng nhau. Ví dụ như các mẫu dữ liệu thuộc vào cùng một cluster chẳng hạn.
- H2 - Cluster Assumptions: Feature space sẽ bao gồm các vùng dày đặc (densse region) và các vùng thưa thớt (sparse region). Các vùng dày đặc sẽ tập trung lại thành 1 cụm và các sample thuộc vào cùng 1 cụm được kì vọng là sẽ có nhãn giống nhau.
- H3 - Low-density Separation Assumptions Ranh giới quyết định (decision boundary) giữa các lớp có xu hướng nằm trong các vùng thưa thớt (spare regions), mật độ thấp (low density regions), bởi vì nếu không, ranh giới quyết định sẽ cắt một cụm mật độ cao (high-density cluster)_ thành hai lớp, tương ứng với hai cụm, làm mất hiệu lực H1 và H2.
- H4: Manifold Assumptions: Giả thuyết này nói rằng các dữ liệu ở không gian chiều cao hơn có thể biểu diễn được dưới các đa tạp - manifold chiều thấp hơn. Để hiểu rõ hơn về manifold trong học máy các bạn có thể tham khảo bài viết sau đây. Giả thuyết H4 là cơ sở cho việc học biểu diễn representation learning giúp tìm ra các đặc trưng biểu diễn cho các dữ liệu có số chiều cao như hình ảnh ... trong một không gian biểu diễn có số chiều nhỏ hơn.
Consistency Regularization
Đây là một khái niệm rất quan trọng và cũng rất phổ biến trong khi thực hiện các thuật toán semi-supervised learning. Consistency Regularization hay còn gọi là Consistency Training xuất phát từ một giả định rằng các noise được inject trong dữ liệu (thông qua các phương pháp data augmentation) hoặc từ trong chính mạng nơ ron (thông qua các regularization như dropout) sẽ không làm ảnh hưởng đến kết quả đầu ra của mô hình. Hay nói cách khác, mô hình cần robusst với những nhiễu loạn trong dữ liệu đầu vào. Phương pháp này được lấy cảm hứng từ các thuật toán self supervised learning như SimCLR, BYOL, SimCSE, etc.. Hi vọng sắp tới sẽ có thời gian để viết thêm nhiều về các hướng này. Tư tưởng chính của chúng là
Các biến đổi khác nhau của cùng một mẫu dữ liệu đầu vào thì phải có cùng một giá trị biểu diễn
Chúng ta sẽ cùng tìm hiểu một số thuật toán áp dụng Consistency Regularization nhé.
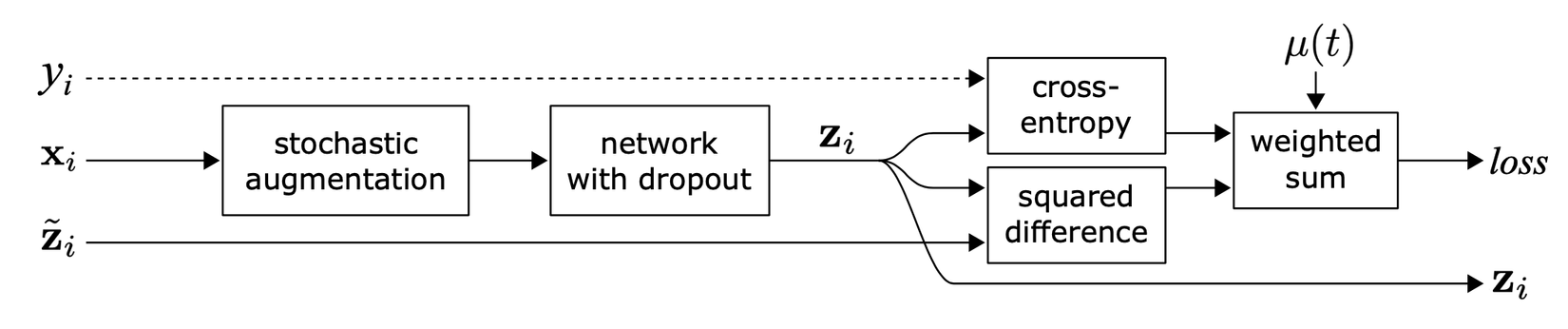
Được giới thiệu trong paper Regularization With Stochastic Transformations and Perturbations for Deep Semi-Supervised Learning các tác giả đề xuất unsupervised loss sử dụng để minimize sự khác biệt giữa hai kết quả của cùng một mẫu dữ liệu khi đưa qua mạng nơ ron với các stochastic transformations (e.g. dropout, random max-pooling). Loss này sẽ không sử dụng nhãn nên có thể áp dụng cho tập dữ liệu không nhãn

Loss của được định nghĩa là MSE giữa hai output kể trên.
Trong đó là một phiên bản của mạng nơ ron gốc với các stochastic augmentation hoặc dropout khác nhau được thêm vào.
Temporal ensembling
Được giới thiệu trong paper Temporal Ensembling for Semi-Supervised Learning cũng lấy cảm hứng từ Π-model. Trong Π-model thì với một mẫu dữ liệu đầu vào chúng ta sẽ cần phải đưa qua mạng 2 lần khiến cho chi phí tính toán tăng cao. Để khắc phục vấn đề này Temporal Ensembling sử dụng đầu ra của mô hình được cập nhật thông qua EMA trong quá trình huấn luyện để làm learning target.
công thức cập nhật cho momentum model khá đơn giản như sau
Trong đó là ensemble prediction tại epoch thứ và là model prediction tại thời điểm huấn luyện. Mẫu số là để normalize giá trị của hàm loss về đúng startup bias.
Mean teachers
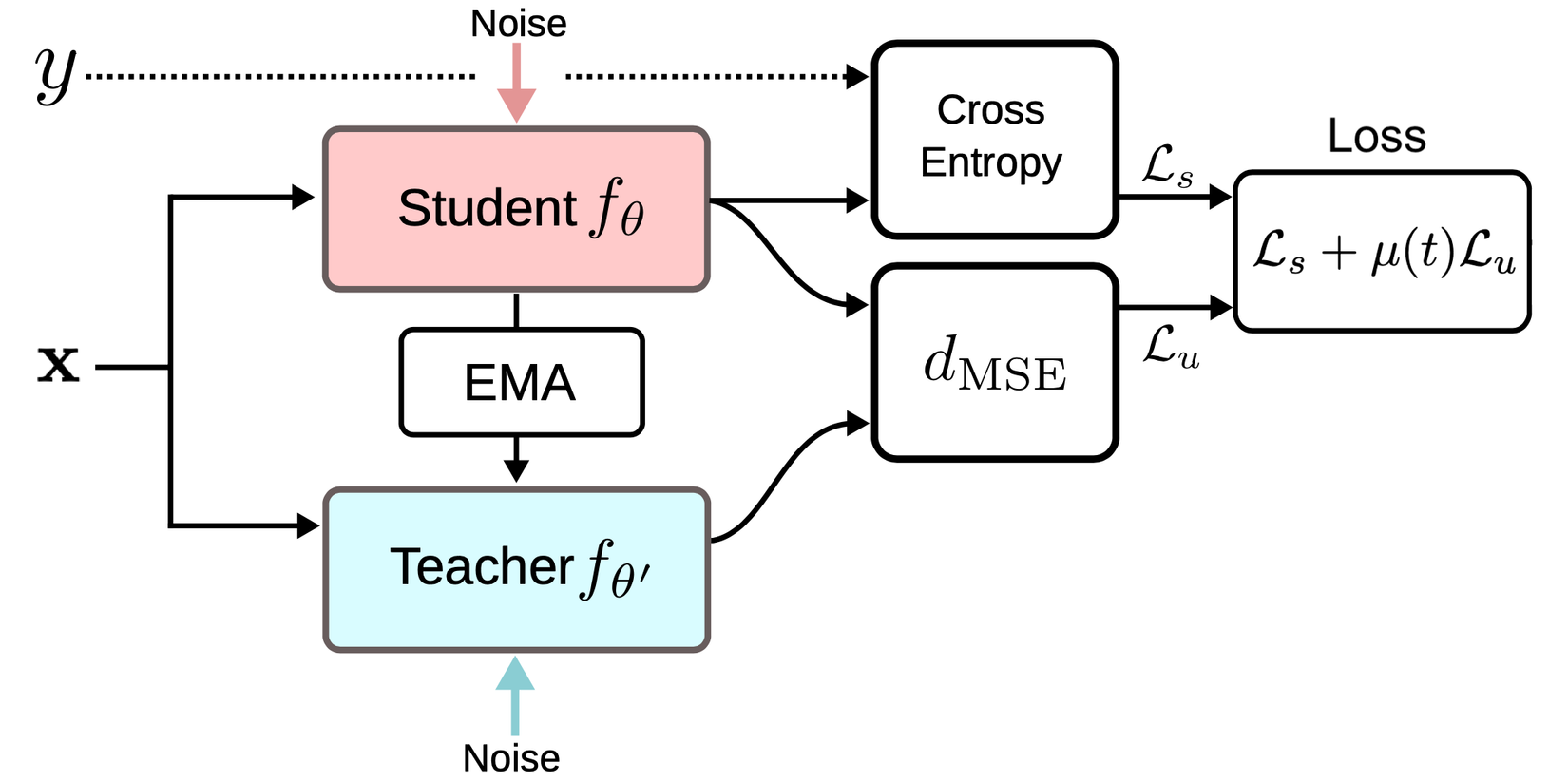
Phương pháp Temporal Ensembling sẽ sử dụng chính model output đã được cập nhật thông qua EMA làm learning target. Tuy nhiên việc cập nhật này chỉ diễn ra sau mỗi epoch dẫn đến mô hình học không có hiệu quả với những tập dữ liệu lớn do label prediction chỉ được cập nhật sau mỗi epoch. Mean teachers là phương pháp được đề xuất trong paper Mean teachers are better role models: Weight-averaged consistency targets improve semi-supervised deep learning results . Phương pháp này sử dụng một phiển bản self-ensembling của chính mô hình hiện tại được cập nhật thông qua exponential moving average (EMA). Đây cũng chính là momentum model mà ta thường thấy trong các nghiên cứu sau này về semi-supervised learning. Mean teachers là paper đã đưa ra khái niệm về momentum model. Thực tế cho thấy phiên bản momentum model này sẽ cho độ ổn định tốt hơn là mô hình gốc. Thay vì cập nhật model outputs thì Momentum model sẽ cập nhật lại toàn bộ weights của mạng thông qua EMA. Việc cập nhật này đơn giản như sau
Trong đó weight của mô hình gốc được coi như student và weight của mô hình momentum được gọi là mean teachers.
Trong mean teachers, consistency regularization loss có mục tiêu minimize student-teacher gap. Mean teachers được kiểm chứng bằng thực nghiệm cho kết quả tốt hơn mô hình student. Chúng ta có thể xem kết quả trong hình sau
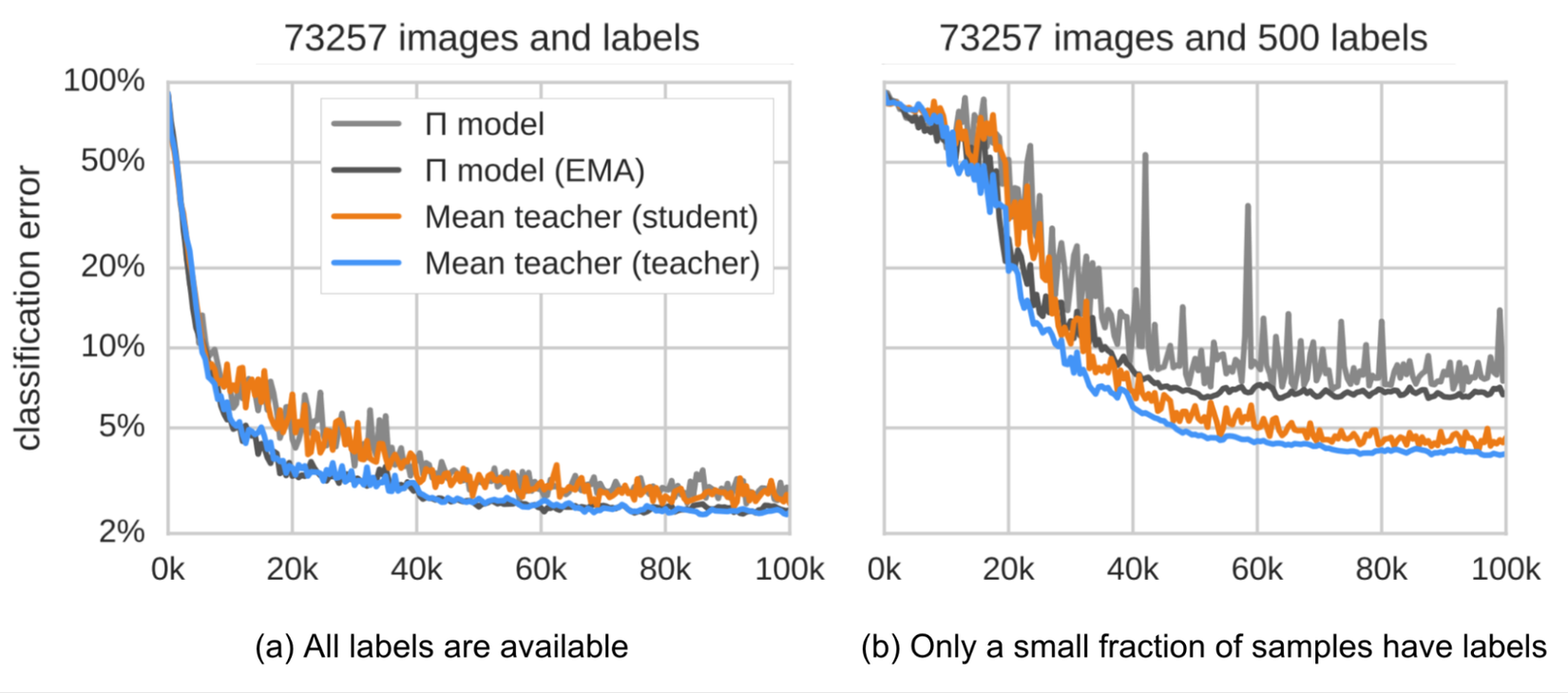
Một số kết luận được rút ra từ mean teachers:
- Input augmentation (e.g. random flips of input images, Gaussian noise) hay student model dropout là cần thiết để đạt được good performance. Tuy nhiên dropout sẽ không cần thiết trong mô hình mean-teachers
- Độ chính xác của mô hình mean-teachers khá nhạy cảm với việc họn hệ số . Thường thì ở giai đoạn đầu tiên hệ số này sẽ được chọn ở mức nhỏ và sẽ càng lớn hơn ở những stage sau bởi lúc này student đã improve khá chậm .
- Tác giả thấy rằng MSE cho kết quả tốt hơn so với các consistency cost functions khác như KL-Divergence.
Adversarial Training
Một vài phương pháp consistency training methods hiện nay được lấy cảm hứng từ việc minimize prediction giữa các phiên bản augmentation khác nhau của cùng một mẫu dữ liệu đầu vào. Tư tưởng này tương tự như trong Π-model tuy nhiên consistency regularization loss sẽ chỉ áp dụng cho unlabeled data.
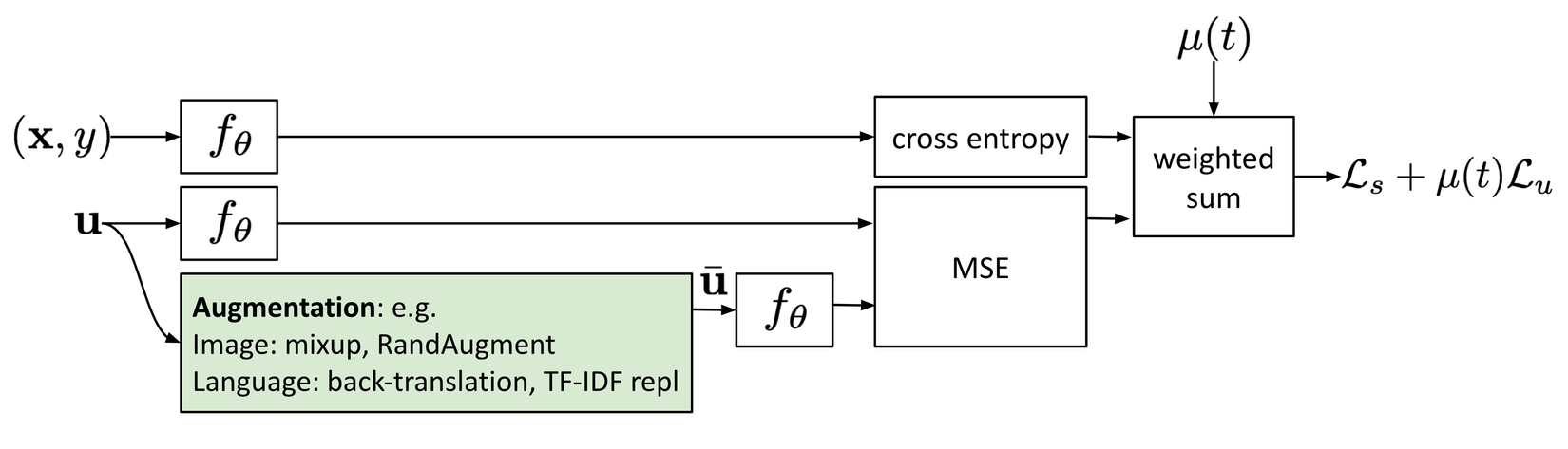
Việc huấn luyện như vậy cũng đã được đề xuất trong các phương pháp Aversarial Training trong paper Explaining and Harnessing Adversarial Examples bằng cách đưa thêm các adversarial noise vào dữ liệu input giúp cho mô hình có thể robust với các adversarial attack. Nó hoạt động khá tốt trên dữ liệu có nhãn.
Trong đó là true distribution, nó xấp xỉ hoá one-hot encoding của ground truth label. là model prediction. là loss function đo lường sự khác biệt giữa hai phân phối.
Virtual Adversarial Training - VAT
Được trình bày trong paper Virtual Adversarial Training: A Regularization Method for Supervised and Semi-Supervised Learning. VAT mở rộng ý tưởng của Adversarial Training với semi-superviosed learning. Bởi trong semi-supervised learning chúng ta sẽ không thể biết được . VAT đã thay thế nó bằng current model prediction của original input với trọng số của mô hình tại thời điểm hiện tại là . Lưu ý rằng đơn giản chỉ là bản copy cứng của model weights và không cập nhật gradient vào
Chúng ta thấy rằng VAT sẽ áp dụng cả labeled và unlabeled data samples.
Interpolation Consistency Training - ICT
Phương pháp này được đề xuất trong paper Interpolation Consistency Training for Semi-Supervised Learning làm giàu thêm dữ liệu bằng cách interpolate các mẫu dữ liệu khác nhau và bắt mô hình phải consistancy với các thay đổi đó. ICT được lấy cảm hứng từ Mixup để thực hiện mix hai sample images thông qua weighted và label smoothing được sử dụng để làm ground truth cho mô hình. Lấy cảm hứng từ Mixup, ICT expect prediction của model với input là mixup image cũng phải tương tự với việc interpolate từ 2 mẫu độc lập.
Trong đó chính là momentum model của
Tư tưởng chính của nó được thể hiện trong hình sau
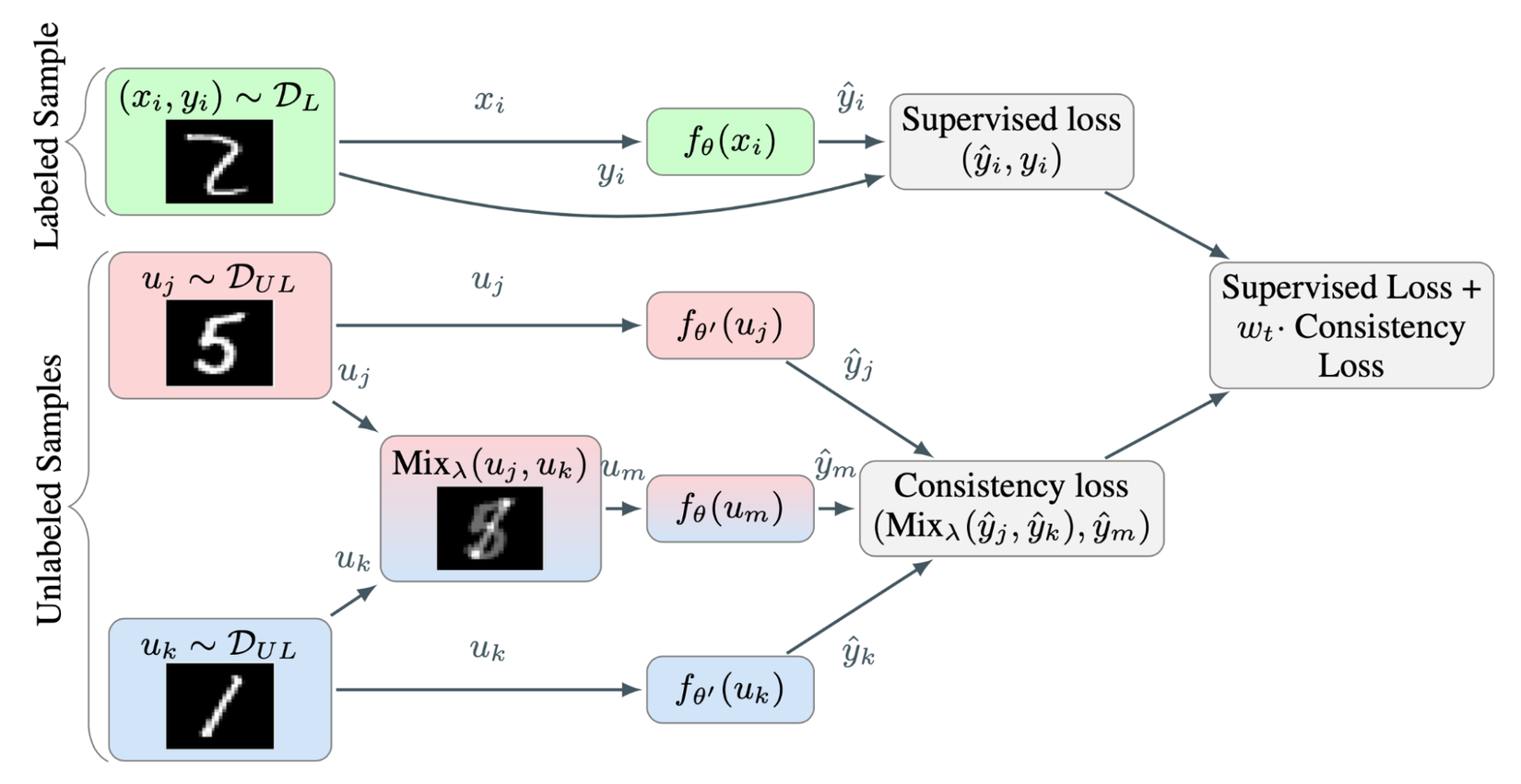
Có thể nhận thấy rằng xác suất để hai samples được lựa chọn để interpolation có cùng một nhãn là khá thấp. (Ví dụ với dataset 1000 classs như image net). Dựa vào gỉa thuyết Low-density Separation Assumptions đã bàn ở các phần trên. Decision boundary thường có xu hướng tập trung tại các low density regions. Hàm loss của ICT như sau
trong đó là phiên bản EMA của
Pseudo Labeling
Lần đầu tiên được giới thiệu trong paper Pseudo-Label : The Simple and Efficient Semi-Supervised Learning Method for Deep Neural Networks năm 2013, phương pháp này gán các fake labels cho các dữ liệu không có nhãn dựa vào maximum softmax probabilities được dự đoán bởi mô hình hiện tại. Sau đó cả dữ liệu không nhãn và có nhãn được tổng hợp lại để huấn luyện mô hình theo chiến lược tương tự như huấn luyện dữ liệu có nhãn.
Có một câu hỏi là tại sao việc sử dụng pseudo label như vậy lại hoạt động? Pseudo label về bản chất tương đương với Entropy Regularizaiton được đề cập trước đó trong paper Semi-supervised Learning by Entropy Minimization từ những năm 2004. Nó cực tiểu hoá conditional entropy của các class probabilities đối với dữ liệu không nhãn giúp cho decision boundary giữa các class có low density. Hay nói các khác, việc minimize entropy giúp giảm sự overlap giữa các class và giúp các decision boundary phân tách rõ ràng hơn.
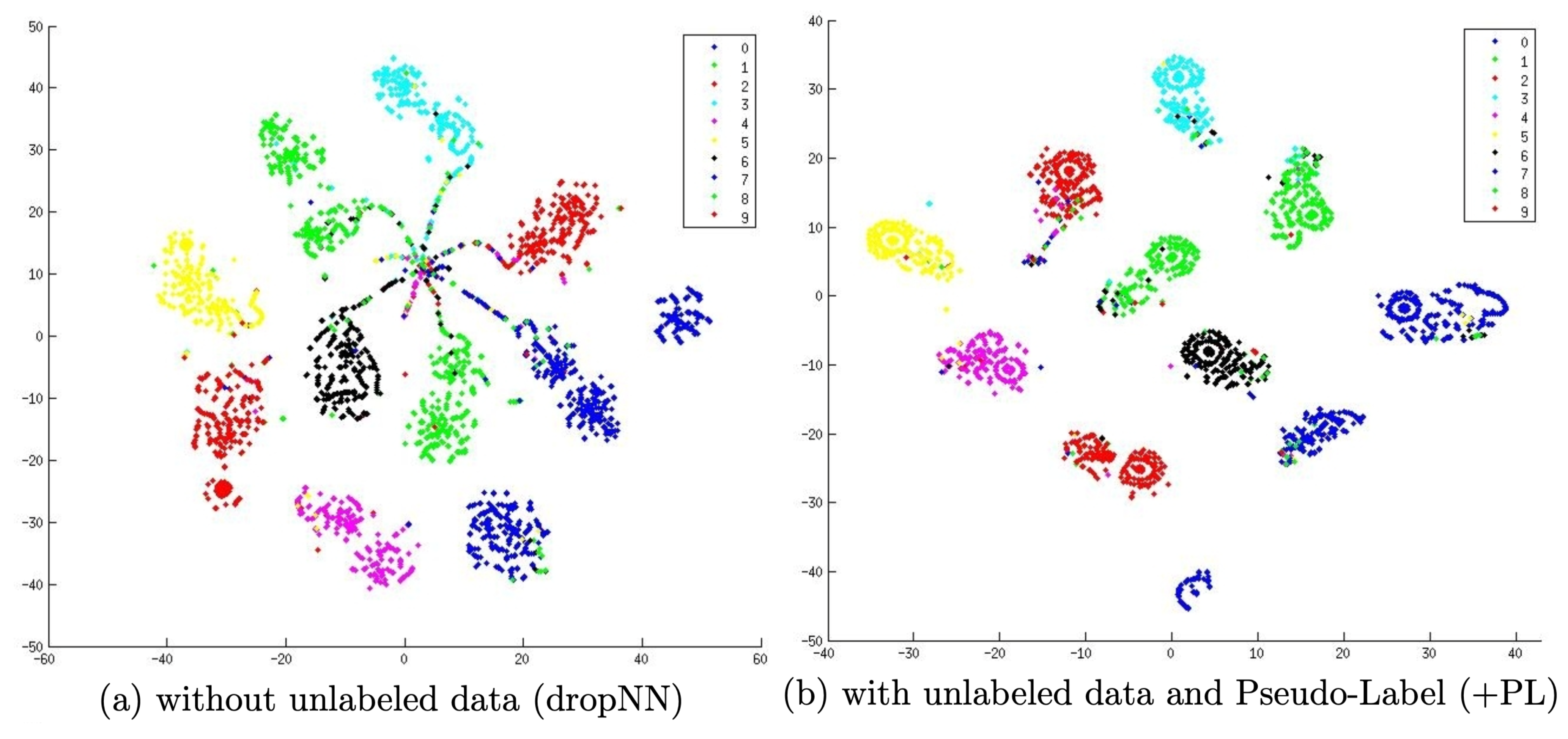
Huấn luyện với pseudo labeling thường là một quá trình được lặp lại với nhiều iterations trong đó mô hình sử dụng để sinh nhãn giả được gọi là mô hình teacher và mô hình học với nhãn giả được sinh ra được gọi là mô hình student. Chúng ta sẽ cùng tìm hiểu một số thuật toán ứng dụng của Pseudo Labeling
Self Training với Noisy Student
Self training không phải là một khái niệm mới. Thậm chí nó đã xuất hiện từ những năm 60 của thế kỉ trước Scudder 1965. Đây là một iterative algorithm trong đó các bước sau được thực hiện lặp đi lặp lại trong suốt quá trình huấn luyện:
- Khởi tạo và huấn luyện môt mô hình trên dữ liệu có nhãn
- Sử dụng mô hình vừa huấn luyện để sinh nhãn giá cho dữ liệu không nhãn
- Lựa chọn các most confidence sample bổ sung vào tập dữ liệu có nhãn
- Lặp lại bước 1
Một bài báo nổi tiếng gần đây đó là Xie et al. (2020) đề xuất mô hình Noisy Student đánh bại các phương pháp supervised trước đó trên cuộc thi ImageNet Classification. Để tạo mô hình teacher, họ huấn luyện EfficientNet (Tan & Le 2019) trên tập ImageNet sau đó sử dụng mô hình này để sinh nhãn giả cho tập dữ liệu gồm 300 triệu ảnh không có nhãn. Một mạng student có kích thước lớn hơn với mạng teacher được sử dụng để huấn luyện semi-supervised learning với các noise được inject vào trong data (thông qua augmentation) và trong model (thông qua dropout và max pooling). Có một vài điểm cần chú ý của phương pháp này như sau:
- Kích thước của student phải thực sự lớn để có thể học được nhiều partern phức tạp hơn từ dữ liệu không nhãn
- Đồi hỏi dữ liệu phải có sự cân bằng giữa các class, đặc biệt là việc cân bằng số lượng các mẫu dữ liệu có chứa nhãn giả ở mỗi class.
- Soft label cho kết quả tốt hơn là hard label
Một diểm thú vị là Noisy Student cũng thể hiện rằng nó có khả năng chống lại các adversarial robustness như FGSM (Fast Gradient Sign Attack)
Reducing Confirmation Bias
Confirmation Bias là một trong những vấn đề gặp phải khi huấn luyện semi supervised learning. Vấn đề này xảy ra khi nhãn giả được sinh ra bởi một mô hình teacher chưa đủ tốt. Việc overfiting trên các nhãn giả sai có thể dẫn đến việc mô hình student học không tốt.
Để reduce confirmation bias, Arazo et al. (2019) đề xuất 2 kĩ thuật để khắc phục tình trạng này. Thứ nhất đó là áp dụng Mixup với soft-labels. Với hai mẫu dữ liệu đầu vào và hai pseudo label tương ứng là . Khi áp dụng Mixup, các interpolated label sẽ được sử dụng để tính toán Cross Entropy Loss thông qua softmax output.
Tuy nhiên MixUp là không đủ nếu như chúng ta chỉ có một số lượng dữ liệu có nhãn quá ít. Các tác giả đề xuất oversampling các mẫu có nhãn trong một mini-batch để đạt được số lượng dữ liệu có nhãn theo một tỉ lệ nhất định
Meta Pseudo Label
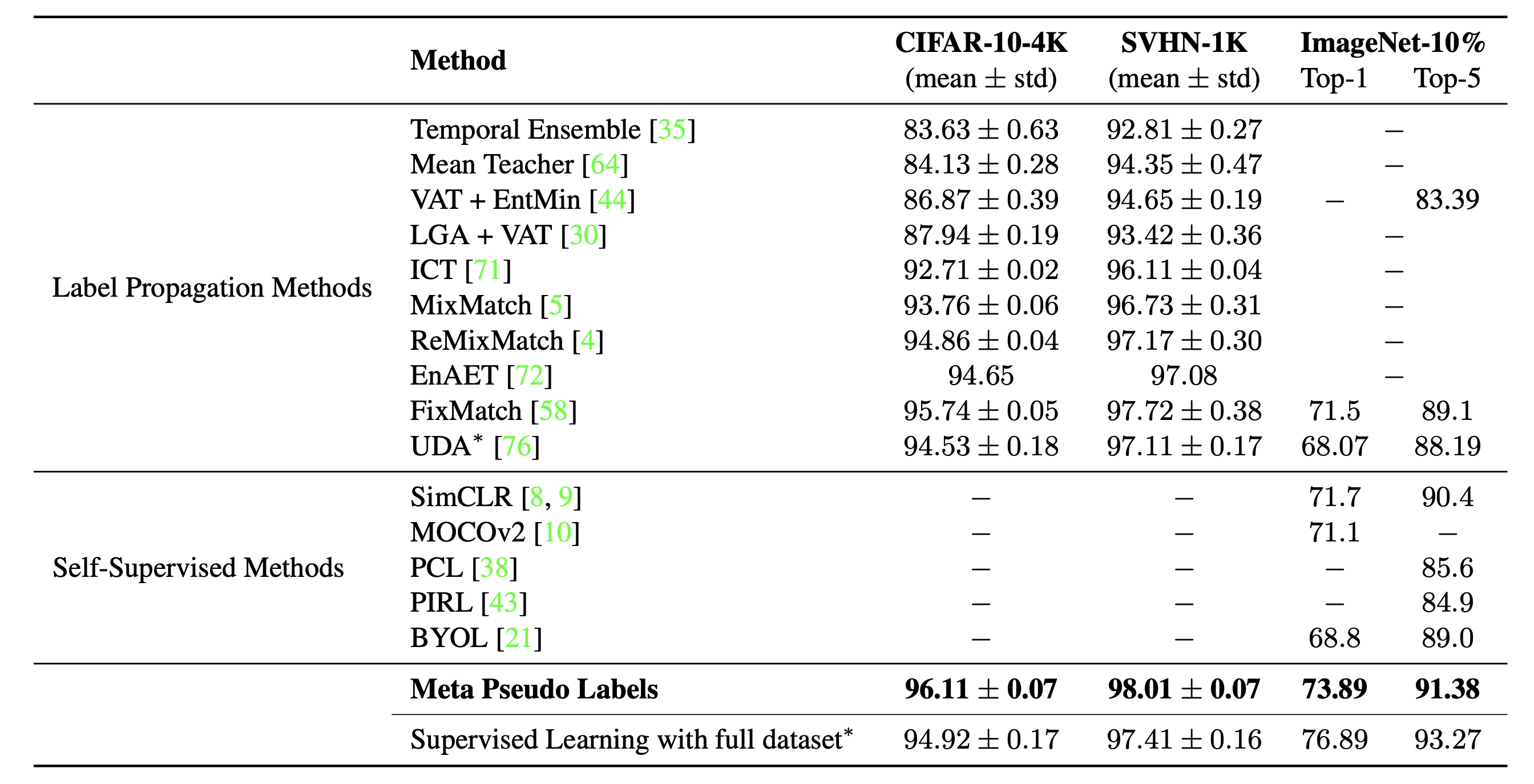
Được trình bày trong nghiên cứu của Pham et al. 2021 đạt được kết quả SOTA vượt qua Pseudo Labels trong việc phân loại hình ảnh trên ImageNet với 90.2% accuracy. Cũng giống như Pseudo Labels, Meta Pseudo Label cũng bao gồm mô hình teacher để xsinh nhãn giả để huấn luyện mô hình student. Tuy nhiên nó khác với Pseudo Labels đó là teacher sẽ được liên tục thích nghỉ với các feedback của student performance trên tập dữ liệu có nhãn. Điều này giúp cho teacher có thể sinh ra các mẫu dữ liệu có chất lượng tốt hơn để dạy cho student.
Giả sử trọng số của teacher và student lần lượt là và . Loss của mô hình student trên dữ liệu có nhãn được định nghĩa như một hàm của và chúng ta có thể cực tiểu hoá hàm loss này bằng các tối ưu mô hình teacher cho phù hợp:
Tuy nhiên để bài toán tối ưu phương trình trên là không tầm thường. Để có thể thực hiện được việc tính toán đạo hàm, tác giải sử dụng một ý tưởng được trình bày trước đó về meta learning MAML, nhằm xấp xỉ hoá multi-step bằng one-step gradient .
Chú ý rằng khi sử dụng soft-label thì công thức trên hoàn toàn khả vi và có thể sử dụng back-propagation để tính toán đạo hàm như thông thường. Tuy nhiên với hard label thì hàm này không khả vi và cần phải sử dụng REINFORCE như đề xuất của tác giả.
Quá trình tối ưu hoá có thể thực hiện luân phiên giữa hai mô hình:
- Student update: Cho một batch các unlabeled samples tiến hành sinh nhãn giả cho và tối ưu trọng số bằng one step SGD
- Teacher update Cho một batch của labeled samples , sử dụng lại optimizer của student để optimize mô hình teacher . Thêm vào đó UDA objective được sử dụng để áp dụng cho mô hình teacher để incorporate consistency regularization.
Kết quả của Meta Pseudo Label khá ấn tượng, đạt được SOTA trên cuộc thi ImageNet
Pseudo Labeling with Consistency Regularization
Chúng ta hoàn toàn có thể sử dụng kết hợp cả hai kĩ thuật nói trên vào trong bài toán semi-supervised và sau đây là một vài thuật toán tiêu biểu cho hướng kết hợp này
MixMatch
MixMatch (Berthelot et al. 2019), là một hướng tiếp cận tổng hợp cho semi-supervised learning giúp tận dụng các nguồn dữ liệu không có nhãn bằng sự kết hợp các kĩ thuật
- Consistency regularization: Như đã trình bày bên trên, mục tiêu của phương pháp này là giúp cho dầu ra của mô hình có độ tương đồng giữa sample gốc và các perturbed version của unlabeled samples.
- Entropy minimization: Lựa chọn các mẫu có kết quả dự đoán tự tin nhất
- MixUp Augmentation: Giúp cho mô hình có linear behaviour giữa các samples như đã trình bày ở phần trên.
Tư tưởng chính của MixMatch, giả sử chúng ta có một batch dữ liệu có nhãn và không nhãn . Chúng ta tạo một augmented version của chúng thông qua thu được và chứa các augmented samples và các guessed labels cho các mẫu dữ liệu không nhãn
Trong đó là sharpening temperature để giảm sự overlap giữa các guessed label. là số lượng các augmentations generated từ mỗi unlabeled example, là tham số của MixUp.
Cho mỗi mẫu không nhãn , MixMatch sinh ra augmentation và pseudo label được dự đoán bằng trung bình
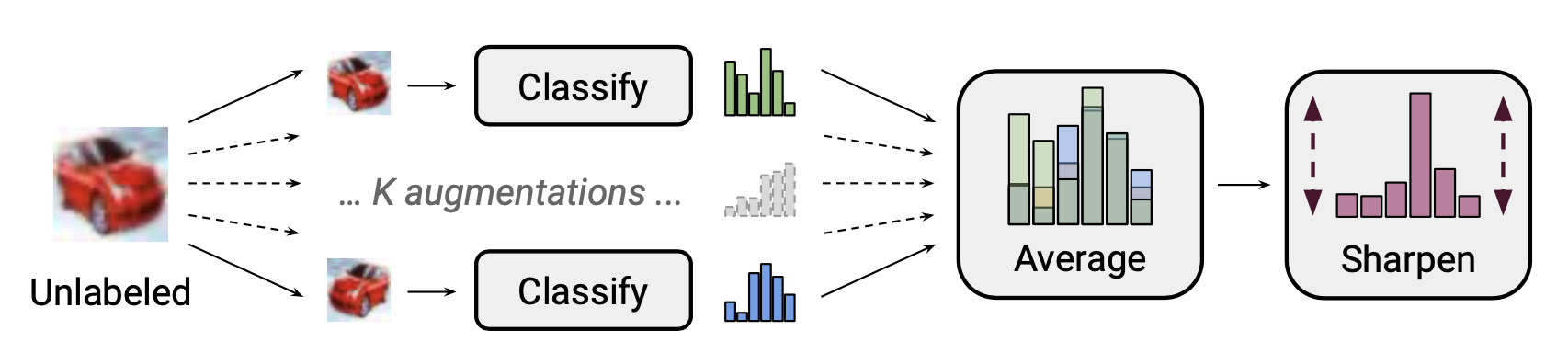
Theo nghiên cứu của họ, điều quan trọng là phải có MixUp đặc biệt là trên dữ liệu không nhãn. Việc loại bỏ sharpen temperture trên phân phối nhãn giả làm ảnh hưởng đến hiệu suất khá nhiều. Average over multiple augmentations cho label guesing cũng đóng một vai trò rất quan trọng.
FixMatch
FixMatch (Sohn et al. 2020) sinh nhãn giả cho dữ liệu có nhãn với weak augmentation và chỉ giữ lại các high confidences samples. Tác giả nhận thấy rằng chính các weak augmenattion và high confidence sẽ giúp cho các nhãn giả trở nên đáng tin cậy hơn. Sau đó, FixMatch học cách dự đoán các nhãn giả này bằng một mẫu được strong augmentation.
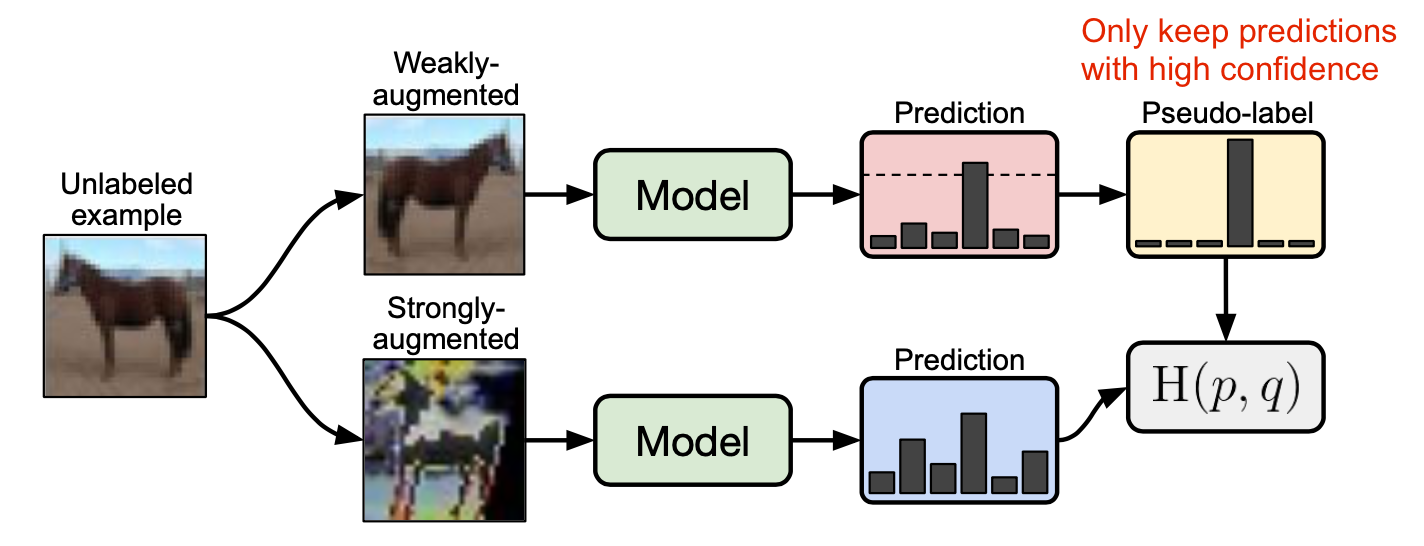
Hàm loss của FixMatch được thể hiện như sau:
Trong đó là pseudo label cho các dữ liệu không nhãn, là hyperparameter thể hiện tỉ lệ tương đối của và
- Weak Augmentation là phép flip và shift augmentation cơ bản
- Strong Augmentation bao gồm các phương pháp AutoAugment, Cutout, RandAugment, CTAugment
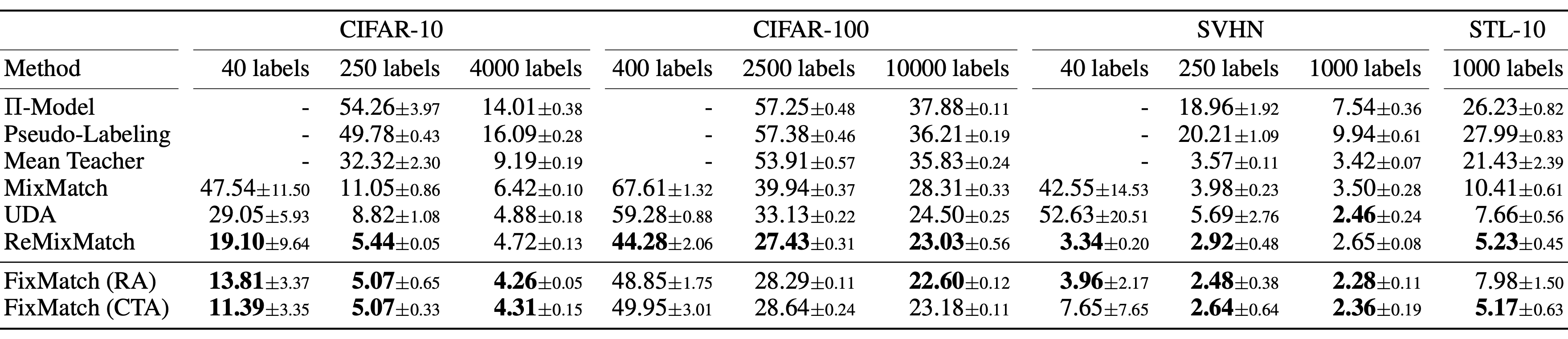
Theo nghiên cứu của FixMatch:
- Sharpening the predicted distribution with a temperature parameter không quá ảnh hưởng nếu như threshold được sử dụng.
-
- Cutout và CTAugment as part of strong augmentations là cần thiết để đạt được good performance.
- Khi thay thế weak augmentation cho label guessing bằng strong augmentation mô hình sẽ bị diverge trong quá trình training và nếu như loại bỏ hoàn toàn weak augmentation thì mô hình sẽ bị overfit trên guessed label.
- Sử dụng weak thay vì strong augmentation cho pseudo label prediction sẽ cho ra các kết quả không ổn định. Strong data augmentation là yếu tố quan trọng trong sự thành công của FixMatch.
Kết luận
Semi-supervised learning là một trong những kĩ thuật rất tiềm năng và rất phù hợp để ứng dụng trong thực tế khi mà lượng dữ liệu có nhãn của chúng ta không đủ. Mặc dù hiện tại các kĩ thuật semi-supervised learning vẫn đang được phát triển và bổ sung thêm nhiều hướng mới tuy nhiên việc hiểu được các tư tưởng và thuật toán nền tảng sẽ giúp chúng ta dễ dàng áp dụng hơn. Hi vọng bài viết này sẽ giúp ích cho các bạn. Hẹn gặp lại các bạn trong các bài viết tiếp theo.
All rights reserved
