Làm gì khi mô hình học máy thiếu dữ liệu có nhãn - Phần 1 - Tổng quan về Active Learning
Bài đăng này đã không được cập nhật trong 3 năm
Lời mở đầu
Xin chào các bạn. Lâu lắm rồi mình mới quay lại viết một bài viết mới. Nhân dịp Viblo tổ chức sự kiện Mayfest2022, mình xin được chia sẻ một số bài viết về chủ đề Làm gì khi các mô hình học máy thiếu dữ liệu có nhãn. Như chúng ta đã biết, dữ liệu là linh hồn của mọi dự án học máy và sẽ chẳng thể có mô hình nào hoạt động tốt nếu như không có một tập dữ liệu chất lượng cả. Nhưng có một vấn đề khác biệt khác lớn giữa các nghiên cứu và thực tế đó chính là các nghiên cứu thường thực hiện thí nghiệm trên các tập dữ liệu nhất định và đã được gán nhãn bởi con người từ trước đó. Trong thực tế đôi khi chúng ta không có đủ dữ liệu có nhãn để huấn luyện, chi phí gán nhãn để có được dữ liệu có nhãn là khá tốn kém. Nên câu hỏi đặt ra là cần phải biết được các sample nào là cần thiết để gán nhãn giúp cho mô hình học được hiệu quả tốt nhất. Active Learning là chiến lược để lựa chọn các sample như thế. Có rất nhiều hướng tiếp cận nhưng trong bài này chúng ta sẽ cùng tìm hiểu một phương pháp đó là Active Learning hay còn gọi là học chủ động. Mình tất nhiên sẽ không thể đi hết tất cả các phương pháp Active Learning hiện nay nhưng sẽ nói qua một chút về tư tưởng chính cũng như một số phương pháp tiêu biểu khi tiếp cận đồng thời minh hoạ trên một tập dữ liệu kinh điển đó là MNIST. Các bạn hẳn sẽ rất bất ngờ với kết quả của nó đấy. OK không còn chần chừ gì nữa chúng ta sẽ bắt đầu ngay thôi
Các kí hiệu
Để thuận tiện cho việc mô tả các thuật toán trong bài viết này, chúng ta sẽ cùng nhau dịnh nghĩa một số kí hiệu cần thiết. Đừng quá lo lắng nếu như bạn không phải là người thích các kí hiệu toán, mọi thứ mình sẽ cố gắng giải thích một cách dễ hiểu nhất các bạn nhé. Sau đây là bảng kí hiệu
| Kí hiệu | Ý nghĩa |
|---|---|
| Số lượng của các unique class | |
| Tập dữ liệu có nhãn, y là biểu diễn one-hot của true label | |
| Tập dữ liệu không nhãn | |
| Toàn bộ tập dữ liệu bao gồm tập có nhãn và không có nhãn | |
| Bất kể sample nào trong tập dữ liệu (kể cả có nhãn hoặc không nhãn) | |
| Sample thứ | |
| Scoring function cho Active Learning | |
| Một bộ phân loại với parameter với đầu ra softmax | |
| Dự đoán có độ tự tin cao nhất của mô hình | |
| Ngân sách cho việc label (số lượng dữ liệu tối đa có thể gán nhãn) | |
| Batch size |
Active Learning là gì?
Nếu bạn nào đã từng tham gia estimate dự án thì hẳn một câu hỏi mà chúng ta cần phải làm rõ đấy là Liệu chúng ta sẽ cần bao nhiêu mẫu dữ liệu để đạt được mô hình có hiệu suất như kì vọng? hay tóm lại là Tôi cần dành bao nhiêu tiền và thời gian cho việc gán nhãn dữ liệu?. Điều này tưởng chừng đơn giản nhưng lại không hề đơn giản một chút nào đâu nhé. Các bạn biết rằng có những loại dữ liệu có thể dễ dàng gán nhãn bởi con người. Có những dạng dữ liệu rất dễ gán nhãn như việc phân loại chó mèo chẳng hạn

Tuy nhiên có một số dạng dữ liệu cực kì khó gán nhãn và đồi hỏi nhiều công sức cũng như kinh nghiệm của các chuyên gia. Ví dụ như ảnh y tế chẳng hạn, hãy thử nhìn bức ảnh sau xem. Nếu bạn có thể ngay lập tức gán nhãn các vùng ung thư trong phổi thì chắc hẳn bạn là một chuyên gia chẩn đoán hình ảnh hàng đầu rồi.
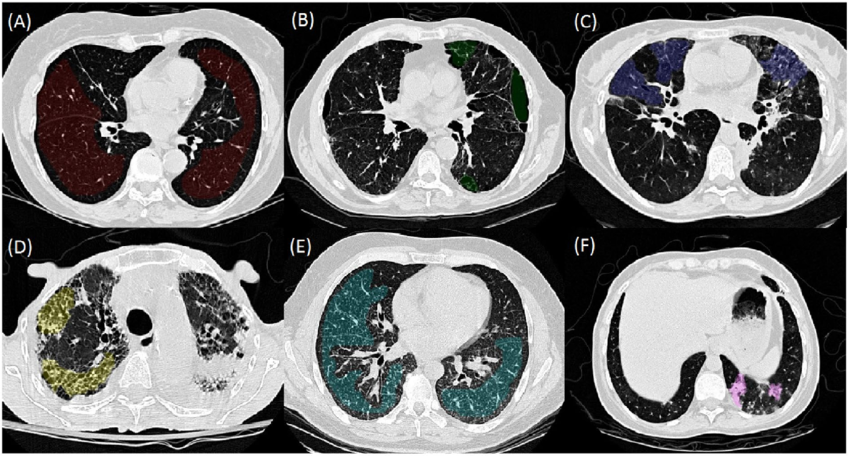
Vậy một vấn đề đặt ra đó là LÀM SAO ĐỂ CÓ MỘT TẬP DỮ LIỆU CHẤT LƯỢNG VỚI CHI PHÍ THẤP NHẤT. Và đó chính là lúc chúng ta có thể nghĩ đến Active Learning.
Active Learning có thể được định nghĩa như sau.
Cho một tập dữ liệu không có nhãn và một ngân sách gán nhãn . Active Learning là phương pháp lựa chọn ra một tập hợp gồm sample từ để gán nhãn sao cho mô hình đạt được hiệu quả tốt nhất.
Đây là một phương pháp rất hiệu quả khi số lượng dữ liệu có nhãn là hạn chế và công sức để gán nhan dữ liệu là lớn ví dụ như bài toán medical image như mình nói phía trên.
Để thống nhất, chúng ta giả sử bài toán đang xét là bài toán phân loại class. Một mô hình phân loại với bộ tham số cho đầu ra là một phân phối xác suất với giá trị dự đoán có độ tự tin nhất là .
Human in loop machine learning
Human in loop learning là một tập hợp các chiến lược nhằm kết hợp giữa con người và các thuật toán học máy nhằm thực hiện một hoặc đồng thời các mục tiêu sau:
- Tăng cường độ chính xác của mô hình học máy
- Đạt đến mục tiêu (có thể về độ chính xác) cho mô hình học máy một cách nhanh chóng hơn
- Kết hợp giữa tri thưc của con người vào các ứng dụng ML
- Hỗ trợ các tác vụ thủ cộng của con người bằng các thuật toán ML nhằm tăng tốc độ xử lý
 Bây giờ chúng ta sẽ đi sâu hơn một chút nhé, rõ ràng là để lựa chọn một cái gì đó thì cần phải có tiêu chí phải không nào. Ví dụ như bạn muốn tìm một cô bạn gái lý tưởng với đầy đủ các tiêu chí xinh, ngoan, giỏi, giàu chẳng hạn. Tất cả mọi thứ cần phải được định lượng rõ ràng (hihi, cái này ví dụ cho vui thôi nhé mọi người) và lựa chọn một mẫu dữ liệu chất lượng thì chắc chắn phải cần có một hàm để đo độ chất lượng. Hầm đó chúng ta gọi là Acquisition Function. Chúng ta có thể định nghĩa như sau:
Bây giờ chúng ta sẽ đi sâu hơn một chút nhé, rõ ràng là để lựa chọn một cái gì đó thì cần phải có tiêu chí phải không nào. Ví dụ như bạn muốn tìm một cô bạn gái lý tưởng với đầy đủ các tiêu chí xinh, ngoan, giỏi, giàu chẳng hạn. Tất cả mọi thứ cần phải được định lượng rõ ràng (hihi, cái này ví dụ cho vui thôi nhé mọi người) và lựa chọn một mẫu dữ liệu chất lượng thì chắc chắn phải cần có một hàm để đo độ chất lượng. Hầm đó chúng ta gọi là Acquisition Function. Chúng ta có thể định nghĩa như sau:
Quá trình định nghĩa các mẫu dữ liệu có gía trị nhất hay cần thiết phải gán nhãn nhất được gọi là chiến lược lấy mấu - sampling strategy. Để thực hiện việc này chúng ta cần có một hàm để định lượng giá trị của một mẫu dữ liệu. Hàm này được gọi là score function hay Acquisition Function và được kí hiệu là . Mẫu dữ liệu nào có giá trị càng cao được kì vọng sẽ có ích hơn cho việc huấn luyện mô hình.
Các phần dưới đây chúng ta sẽ xem xét đến một số chiến lược lấy mẫu điển hình
Uncertainty Sampling
Uncertainty Sampling lựa chọn các mẫu dữ liệu nào mà mô hình cho dự đoán kém tự tin nhất làm các dữ liệu cần phải gán nhãn. Điều này cũng dễ hiểu bởi chúng ta sẽ cần phải bổ sung những mẫu dữ liệu giúp khắc phục các điểm yếu của mô hình hiện tại. Với một mô hình, độ uncertainty có thể được đo bằng đầu ra xác suất dự đoán. Mặc dù điều này trên thực tế đôi khi không hoàn toàn đúng trong mọi trường hợp nhất là đối với các mô hình học sâu. Các mô hình học sâu thường có xu hướng over-confident. Tức là mô hình quá tự tin khi dự đoán một mẫu dữ liệu kể cả dữ đoán đó là sai. Đôi khi chúng ta đưa một ảnh con chó vào mà mô hình vẫn tự tin đoán 99% đây là mèo chẳng hạn.
Có một số cách mà chúng ta có thể lựa chọn như sau:
- Least confident score đơn giản là lựa chọn các mẫu có xác suất đầu ra là thấp nhất.
- Margin score lựa chọn các mẫu mô hình phân vân nhất tức có margin score thấp nhất. Margin score được định nghĩa là độ chênh lệch xác suất giữa class mô hình tự tin nhất và tự tin thứ nhì.
- Entropy Chúng ta cũng có thể sử dụng entropy để đo mức độ uncertainty của mô hình.
Có một phương pháp khác để đánh giá mức độ uncertainty của một sample đó là sử dụng một commitee của các models. Các models này có thể có các kiến trúc khác nhau, được huấn luyện trên tập dữ liệu có nhãn. Chúng ta giả sử có model trong pool với các trọng số lần lượt là . Có các phương pháp thực hiện QBC - Query By Committee như sau:
- Voter Entropy Chúng ta đo trong đó sẽ đếm số lượng votes từ commitee dành cho label y
- Consensus entropy Chúng ta đo trong đó là dự đoán trung bình của các model trong commitee
- KL Divergence Chúng ta đo sự khác biệt về mặt phân phối của từng model riêng lẻ trong commit với trung bình của toàn bộ committee.
Diversity Sampling
Diversity Sampling hướng tới việc tìm kiếm một tập hợp các samples có thể biểu diễn tốt phân phối của dữ liệu hiện tại. Tính chất đa dạng - diversity là rất quan trọng bởi model được kì vọng sẽ hoạt động tốt với mọi loại đầu vào của dữ liệu chứ không chỉ đơn thuần là một tập dữ liệu nhất định. Phương pháp này sẽ định nghĩa các mẫu dữ liệu mà mô hình được coi là underrepresented hay unknown tại curent state. Nó sẽ tìm ra các mẫu dữ liệu chứa các đặc trưng hiếm gặp trong các dữ liệu training hiện tại
Expected Model Change
Expected model change đề cập đến tác động của một mẫu dữ liệu lên mô hình trong quá trình huấn luyện. Tác độ của thể ảnh hưởng đến việc thay đội trọng số của mô hình hoặc giá trị của hàm loss, giá trị của đạo hàm trong quá trình huấn luyện. Thông thường sẽ lựa chọn các mẫu giúp maximize model change.
Deep Acquisition Function
Measuring Uncertainty
Model uncertainty được chia thành hai loại chính như sau:
- Aleatoric uncertainty thường được tạo ra bởi nhiễu trong dự liệu (nhiễu trong thực hiện thí nghiệm, nhiễu do thiết bị). Nó có thể phụ thuộc hoặc không phụ thuộc vào input và thường rất khó giải thích một cách tường minh vì thiếu thông tin của ground truth (điều kiện đo lường, sức khoẻ của người làm thí nghiệm)
- Epistemic uncertainty nói đến độ không ổn định do bản thân mô hình học máy gây ra và thường chúng ta dựa trên giả thiết rằng có ground truth của dữ liệu. Loại uncertainty này về mặt lý thuyết có thể giải quyết được bằng cách bổ sung thêm nhiều dữ liệu và ground truth tương ứng.
Ensemble and Approximated Ensemble
Việc ensemble các mô hình có độ đa dạng khác nhau thường được kì vọng sẽ giúp cải thiện độ chính xác. Đây là một phương pháp khá phổ biến trong học máy. Để đánh giá độ uncertainty đối với các mẫu dữ liệu nhất định thì việc ensemble các trained model được huấn luyện độc lập là một hướng tiếp cận khả thi. Tuy nhiên việc huấn luyện nhiều mô hình Deep Learning là khá tốn kém. Chính vì thế người ta sử dụng một kĩ thuật đó là Dropout để mô phỏng lại việc ensemble giữa các mô hình khác nhau. Chúng ta có thể coi một mô hình duy nhất nhưng với các dropout mask khác nhau trong quá trình forward như các mô hình riêng biệt. Quá trình này được gọi là MC Dropout - Monte Carlo Dropout.
Loss Prediction
Mục tiêu của hàm loss là để huấn luyện mô hình. Giá trị hàm loss thấp nhất thể hiện mô hình có kết quả tốt và chính xác. Thuật toán này đề xuất việc dự đoán giá trị của hàm loss cho các mẫu dữ liệu không có nhãn. Dữ liệu được lựa chọn để gán nhãn là những dữ liệu cho giá trị loss cao. Module loss prediction thường là một mạng MLP đơn giản với dropout
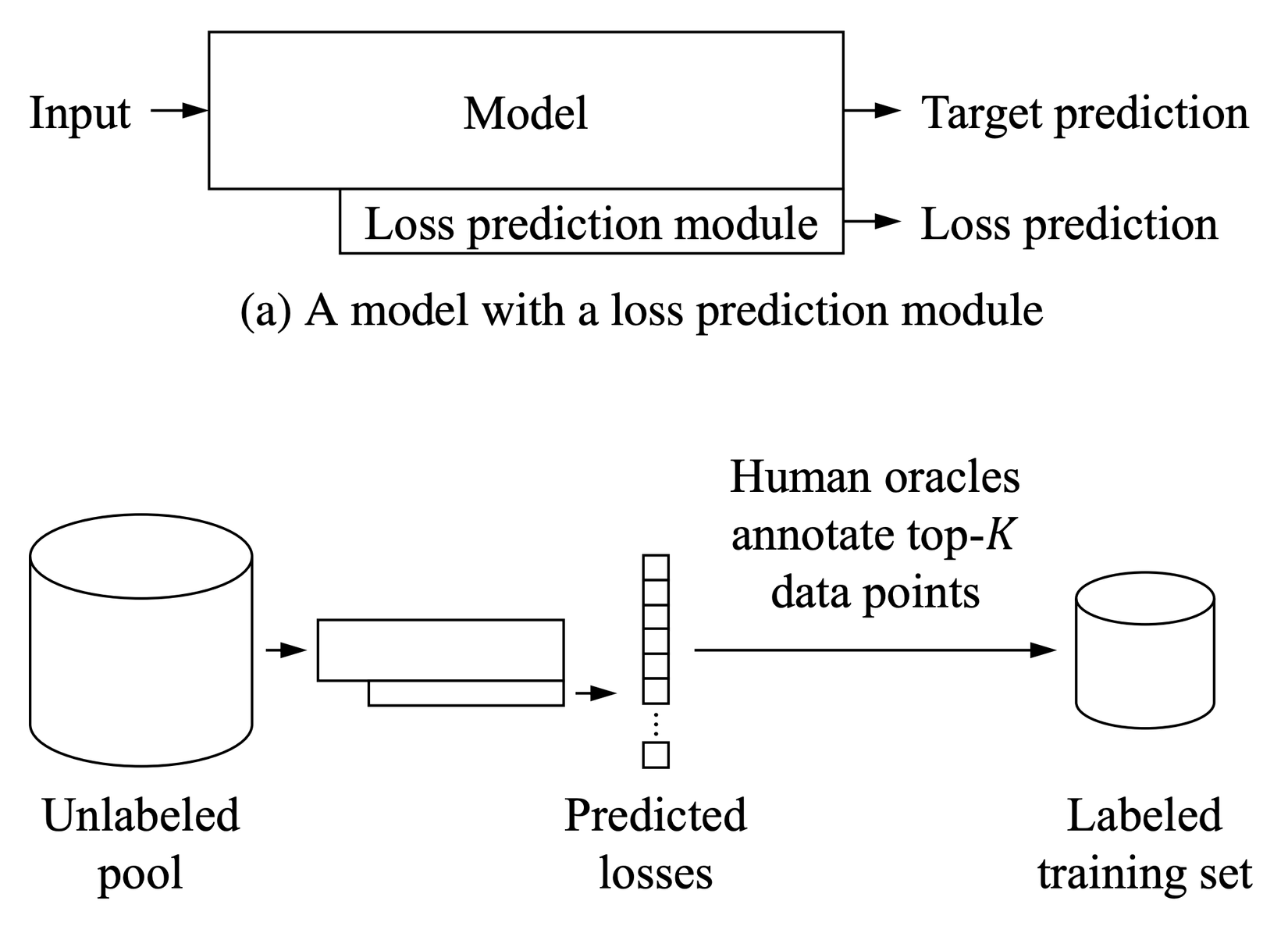
Gọi là đầu ra của loss preidction module và là giá trị true loss. Để huấn luyện module này thì một hàm loss MSE đơn giản chưa hẳn là một lựa chọn tốt bởi giá trị của loss sẽ giảm dần theo thời gian. Một hàm mất mát tốt cần phải độc lập với sự thay đổi về mặt độ lớn của training loss. Để khắc phục được điều đó, người ta đề xuất so sánh trên các cặp dữ liệu. Trong mỗi một batch dữ liệu có kích thước trong đó có cặp của các dữ liệu và mô hình loss prediction sẽ được kì vọng sẽ dự đoán đúng mẫu nào có loss lớn hơn.
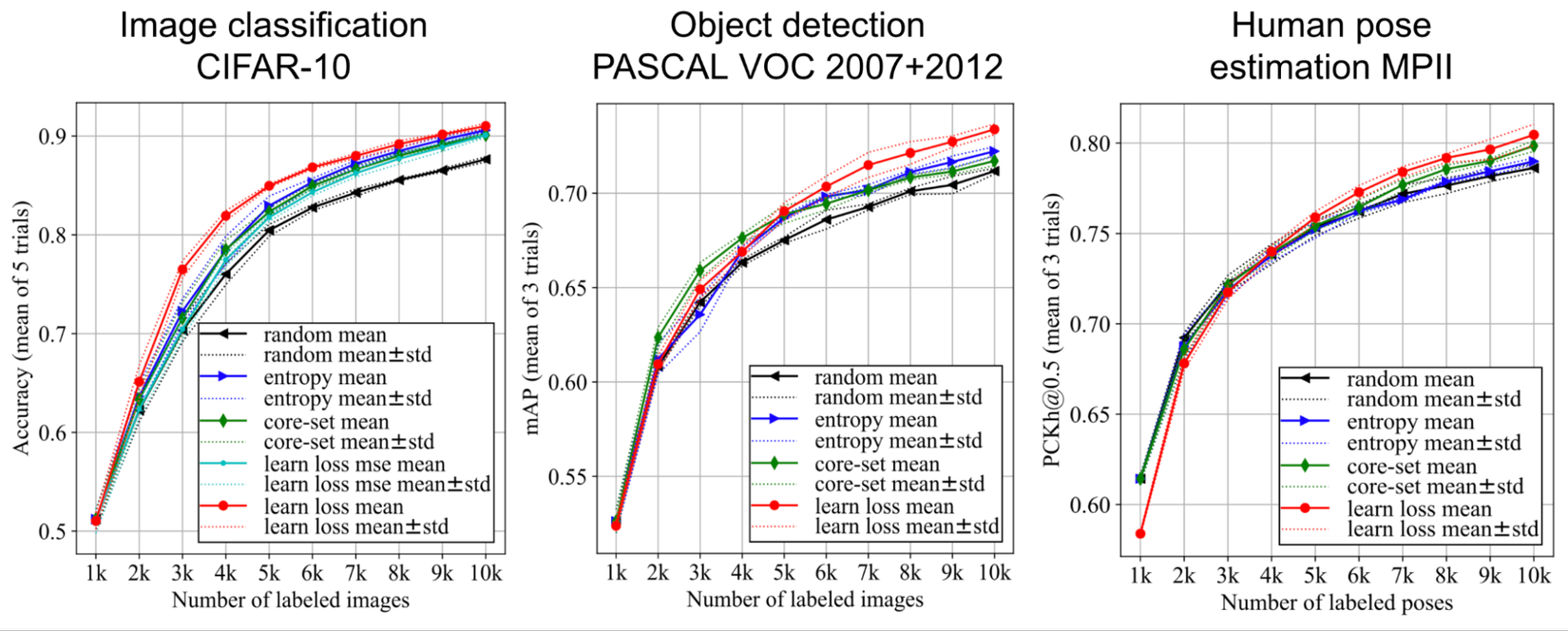
Trong các thử nghiệm thì phương pháp loss prediction cho hiệu quả tốt hơn random base line hay entropy based
Adversarial Setup
VAAL (Variational Adversarial Active Learning) là phương pháp dựa trên GAN trong đó discriminator được huấn luyện để phân biệt dữ liệu không nhãn từ các dữ liệu có nhãn.
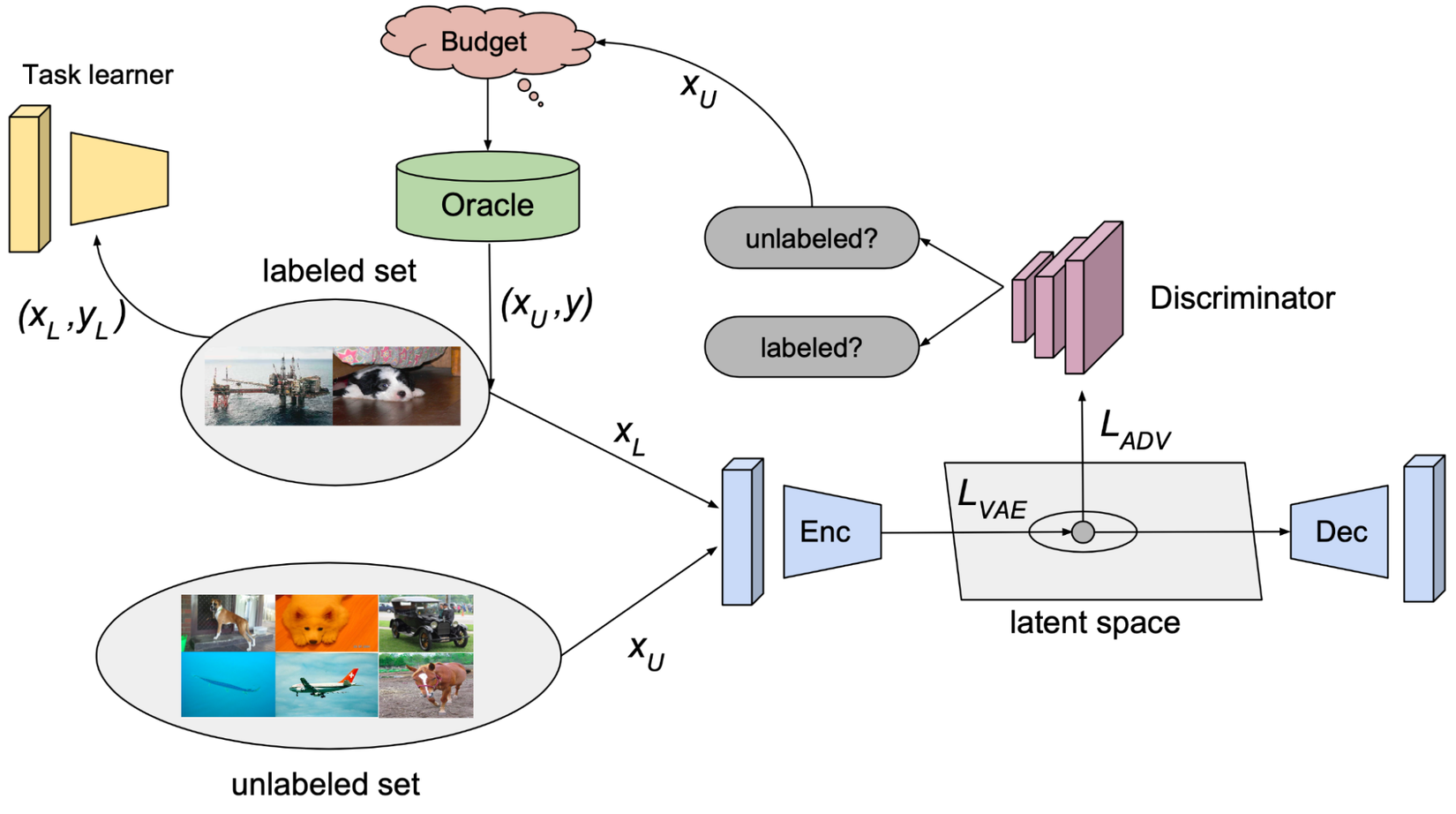
- học biểu diễn giá trị trong latent space của tập dữ liệu có nhãn và không nhãn tương ứng. Mục tiêu của nó là đánh lừa discriminator rằng tất cả các sample đều là dữ liệu có nhãn.
- dự đoán mẫu dữ liệu là có nhãn (1) hoặc không nhãn (0) dựa trên vector biểu diễn . Thuật toán VAAL sẽ lựa chọn unlabeled samples nếu như có discriminator scores thấp. Tức là các mẫu này có sự khác biệt lớn so với các mẫu được được gán nhãn trước đó.
Code thử nghiệm các phương pháp Uncertainty Sampling với MNIST
Như vậy là trong phần trên mình đã điểm sơ qua một chút về lý thuyết để các bạn hiểu tư tưởng chính của active learning là gì? Giờ chúng ta sẽ bắt đầu đi vào code thử nghiệm trên tập MNIST để dễ dàng hình dung các bước thực hiện active learning như thế nào nhé
Phân chia tập dữ liệu
Như các bạn đã biết thì chúng ta sẽ thực hiện active learning trên hai tập dữ liệu là tập có nhãn và tập không có nhãn. Việc cần làm của chúng ta là lựa chọn các mẫu dữ liệu từ tập không nhãn theo các tiêu chí nhất định, gán nhãn rồi bổ sung thêm vào tập dữ liệu có nhãn để tiến hành training tiếp. Về mặt lý thuyết là chúng ta sẽ phải tự gán nhãn thủ công các mẫu đó bằng tay. Nhưng với tập MNIST là tập đã được gán nhãn từ trước thì chúng ta có thể đơn giản công việc này bằng cách chia tập dữ liệu làm 2 phần: có nhãn và phần còn lại chúng ta không động đến label coi như tập không có nhãn. Đầu tiên chúng ta sẽ import các thư viên cần thiết
from __future__ import absolute_import, division, print_function, unicode_literals
# Install TensorFlow
!pip install -q tensorflow==2.0.0
import numpy as np
import tensorflow as tf
import matplotlib as mpl
import matplotlib.pyplot as plt
%matplotlib inline
Sau đó tiến hành phân chia tập dữ liệu theo cách chúng ta đã định nghĩa trước đó
mnist = tf.keras.datasets.mnist
(x_train, y_train), (x_test, y_test) = mnist.load_data()
x_train, x_test = x_train / 255.0, x_test / 255.0
Định nghĩa chiến lược đánh giá Labeling Prioritization
Đánh giá độ chính xác trên tập test khi bổ sung dần dần 500 items, rồi 1,000, rồi 1,500, cho đến khi đủ 20,000 items. Tại mỗi một lần lặp sẽ bổ sung thêm 500 items vào training set dựa vào prioritizer. Hàm prioritizer dựa trên predictions của model trên các unlabeled samples và lựa chọn ra các mẫu có tiềm năng nhất theo từng chiến lược để bổ sung vào tập training
def eval_prioritization_strategy(prioritizer):
train_indices = range(60000)
test_accuracies = []
x_train_subset = np.zeros([0, 28, 28])
y_train_subset = np.empty([0,])
for i in range(40):
selected_indices = train_indices[0:500]
train_indices = train_indices[500:]
x_train_subset = np.concatenate((x_train_subset, x_train[selected_indices,...]))
y_train_subset = np.concatenate((y_train_subset, y_train[selected_indices,...]))
model = tf.keras.models.Sequential([
tf.keras.layers.Flatten(input_shape=(28, 28)),
tf.keras.layers.Dense(128, activation='relu'),
tf.keras.layers.Dense(10, activation='softmax')
])
model.compile(optimizer='adam',
loss='sparse_categorical_crossentropy',
metrics=['accuracy'])
model.fit(x_train_subset, y_train_subset, epochs=5, verbose=0)
loss, accuracy = model.evaluate(x_test, y_test, verbose=0)
test_accuracies.append(accuracy)
print('Training data size of %d => accuracy %f' % (x_train_subset.shape[0], accuracy))
predictions = model.predict(x_train[train_indices,...])
train_indices = prioritizer(train_indices, predictions)
return test_accuracies
Baseline sử dụng random selection samples
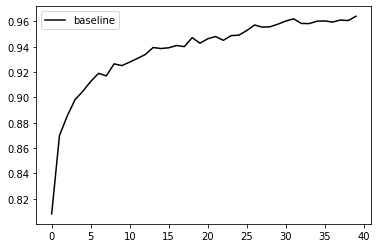
Đơn giản ta chỉ cần bổ sung dần dần dữ liệu có nhãn vào trong tập huấn luyện và ta nhận thấy rằng với khoảng 2500 mẫu mô hình đã có thể đạt độ chính xác 90%. Và khi sử dụng hết 20000 mẫu dữ liệu (giả sử budget gán nhãn là 20000 mẫu) thì độ chính xác tăng lên khoảng 97%
unprioritized_accuracies = eval_prioritization_strategy(lambda indices, pred: indices)
Sau khi chạy chúng ta có thể vẽ biểu đồ thể hiện mức độ tăng độ chính xác của mô hình khi bổ sung dữ liệu theo chiến lược này
plt.plot(unprioritized_accuracies, 'k', label='baseline')
plt.legend()
Chúng ta thu được kết quả như sau
Prioritize "least confidence"
Thay đổi chiến lược thay vì lựa chọn random thì chúng ta lựa chọn các mẫu nào có độ tin cậy thấp nhất để bổ sung thêm vào tập dữ liệu huấn luyện. Có thể thấy chiến lược này mô hình tăng độ chính xác nhanh hơn. Chỉ khoảng 5500 dữ liệu gán nhãn đã có thể đạt được độ chính xác 97% như 20000 mẫu của phương pháp random selection. Điều này giúp tiết kiệm chi phí gán nhãn hơn
def least_confidence_prediction_prioritizer(indices, predictions):
max_logit = list(zip(indices, np.amax(predictions,axis=1)))
max_logit.sort(key=lambda x: x[1]) # sort in ascending order
return list(zip(*max_logit))[0]
least_confidence_accuracies = eval_prioritization_strategy(least_confidence_prediction_prioritizer)
Sau khi chạy thử nghiệm chúng ta cũng vẽ hình để minh hoạ hai phương pháp này
plt.plot(unprioritized_accuracies, 'k', label='baseline')
plt.plot(least_confidence_accuracies, 'b', label='least confidence')
plt.legend()
Kết quả như sau
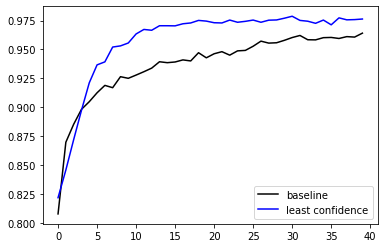
Chúng ta thấy chiến lược lựa chọn bằng least confidence cho hiệu quả hơn hẳn so với random sampling
Prioritize "highest entropy" of the resulting softmax
Tương tự chúng ta cũng thử nghiệm highest entropy để lựa chọn. Kết quả khá tương đồng với least confidence
def entropy_prioritizer(indices, predictions):
p = predictions * np.log(predictions)
p = -p.sum(axis=1)
p = list(zip(indices, p))
p.sort(reverse=True, key=lambda x : x[1]) # sort in descending order
return list(zip(*p))[0]
entropy_prioritized_accuracies = eval_prioritization_strategy(entropy_prioritizer)
Sau đó chúng ta cũng vẽ biểu đồ để so sánh kết quả
plt.plot(unprioritized_accuracies, 'k', label='baseline')
plt.plot(least_confidence_accuracies, 'b', label='least confidence')
plt.plot(entropy_prioritized_accuracies, 'g', label='highest entropy')
plt.legend()
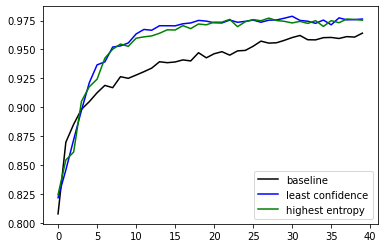
Prioritize "least margin"
Chiến lược này quan tâm để least margin. Margin là độ chênh lệch giữa dự đoán class có độ tin cậy cao nhất và class có độ tin cậy thứ nhì. Khoảng cách này càng nhỏ thì độ phân vân của mô hình càng cao với những dữ liệu này.
def margin_prioritizer(indices, predictions):
p = -np.sort(-predictions) # sort in descending order
p = p[:,0] - p[:,1]
p = list(zip(indices, p))
p.sort(key=lambda x : x[1]) # sort in ascending order
return list(zip(*p))[0]
margin_prioritized_accuracies = eval_prioritization_strategy(margin_prioritizer)
Chúng ta cũng thử vẽ biểu đồ để thuận tiện so sánh cả 4 trường hợp
plt.plot(unprioritized_accuracies, 'k', label='baseline')
plt.plot(least_confidence_accuracies, 'b', label='least confidence')
plt.plot(entropy_prioritized_accuracies, 'g', label='highest entropy')
plt.plot(margin_prioritized_accuracies, 'r', label='least margin')
plt.legend()
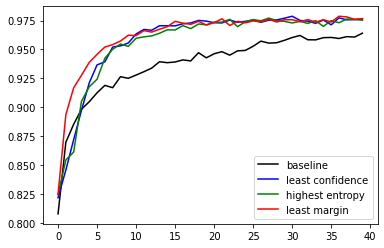
Nhận xét kết quả thí nghiệm
Các kết quả trên chỉ ra rằng với việc lựa chọn các chiến lược gán nhãn tốt sẽ giúp mô hình có thể đạt được 95% test accuracy với chỉ 3,500 samples gán nhãn,trong khi nếu như gán nhãn random chúng ta sẽ cần phải mất khoảng 14,000 samples!
Kết quả của least margin có vẻ tốt hơn so với các phương pháp còn lại tuy nhiên nó chỉ áp dụng được với các bài toán có nhiều hơn 2 lớp.
Kết luận
Active learning là một trong những phương pháp rất hữu hiệu để ứng phó đối với các trường hợp thiếu dữ liệu gán nhãn và chúng ta cần thực hiện việc gán nhãn. Nó giúp cho việc gán nhãn trở nên hữu ích hơn bằng cách tập trung vào các mẫu dữ liệu mà mô hình cần nhất. Đây là một phương pháp rất có ý nghĩa trong thực tế khi mà công sức và chi phí dành cho việc gán nhãn thường là giới hạn. Bài viết này giới thiệu tổng quan về phương pháp Active Learning. Để có thể đi sâu hơn vào từng phương pháp, mình xin hẹn gặp lại các bạn trong các bài viết sau
All rights reserved
