Ủa sao nói UniswapV3 vẫn là constant-product mà có thấy dòng nào trong code đảm bảo $x * y= k$ đâu?

2. Suy luận từ V2 sang V3

2.1. Nhắc lại một chút về V2

Ai cũng biết, công thức toán khi swap của Uniswap là constant-product, nghĩa là: $x*y=k$. Giá trị k trước khi swap và sau khi swap phải được giữ nguyên, k chỉ thay đổi khi có hành động thêm hoặc rút thanh khoản.

Dễ hiểu hơn, ban đầu Pool đang có reserves là $x$ token0 và $y$ token1. Alice muốn swap một lượng $x_0$ token0 lấy một lượng $y_0$ token1. Thì $x_0$ và $y_0$ phải thoả mãn:

$(x + x_0) * (y - y_0) = x * y$

Ví dụ: ban đầu $x = 100$, $y = 48$. Alice muốn swap 20 token0 lấy token1 thì lượng token1 mà Alice nhận được là:

$y_0 = 48 - \frac{4800}{100 + 20} = 8$

Và, thanh khoản của Pool được tính theo công thức:

$L=\sqrt{x*y}$

Mắc đi hát karaoke quá mà ở quê không ai rủ đi.

Tại sao công thức tính L lại là $L = \sqrt{x * y}$ ?

Suy luận một chút, tính chất đầu tiên của L cần phải được thoả mãn là: $L$ phải được giữ nguyên giá trị trước khi swap và sau khi swap. Nếu lấy công thức $L = x + y$, tính chất đó sẽ không thể thoả mãn, mà ta đã có $x* y = k$ (hằng số), do đó L sẽ là một công thức gì đó liên quan đến $x * y$, dạng $L = f(x * y)$.

Tính chất thứ hai mà $L$ cần phải được thoả mãn là tính tỷ lệ, nghĩa là khi một liquidity provider thêm thanh khoản vào Pool, lượng liquidity được ghi nhận cho provider đó phải có tỷ lệ tương xứng với liquidity của tổng Pool dưa trên số lượng token0 và token1 mà provider đó đã thêm vào.

Ví dụ, Pool đang có reserves là $x$ token0 và $y$ token1, có tổng liquidity là $L_{total}$, Alice thêm $x_0$ token0 và $y_0$ token1 vào Pool, liquidity được ghi nhận cho Alice $L_0$, phải thoả mãn:

$\frac{L_0}{L_{total}}=\frac{x_0}{x}$ hoặc $\frac{L_0}{L_{total}} = \frac{y_0}{y}$

Nếu chúng ta sử dụng công thức $L = x * y$, công thức trên không thể thoả mãn, hãy cho các con số vào để dễ hình dung hơn.

$x = 300, y = 600 => L_{total} = 300 * 600 = 180000$

$x_0 = 100, y_0 = 200 => L_0 = 100 * 200 = 20000$

$=> \frac{L_0}{L_{total}} = \frac{20000}{180000} = \frac{1}{9}$

$=> \frac{x_0}{x} = \frac{100}{300} = \frac{1}{3}$ và $\frac{y}{y} = \frac{200}{600} = \frac{1}{3}$

Rõ ràng là công thức $L= x * y$ không thể thoả mãn tính tỷ lệ.

Nếu $L = \sqrt{x * y}$ thì sao? Hãy thử với các con số ở trên:

$x = 300, y = 600 => L_{total} = \sqrt{300 * 600} = \sqrt{180000}$

$x_0 = 100, y_0 = 200 => L_0 = \sqrt{100 * 200} = \sqrt{20000}$

$\frac{L_0}{L_{total}} = \frac{\sqrt{20000}}{\sqrt{180000}} = \frac{1}{3}$

Như vậy, công thức $L= \sqrt{x*y}$ thoả mãn tính tỷ lệ.

Oke, tiếp theo, tại sao lại hoặc giữa $\frac{x_0}{x}$, $\frac{y_0}{y}$. Hãy nhìn vào code một tí, hàm mint() của UniswapV2Pair.sol

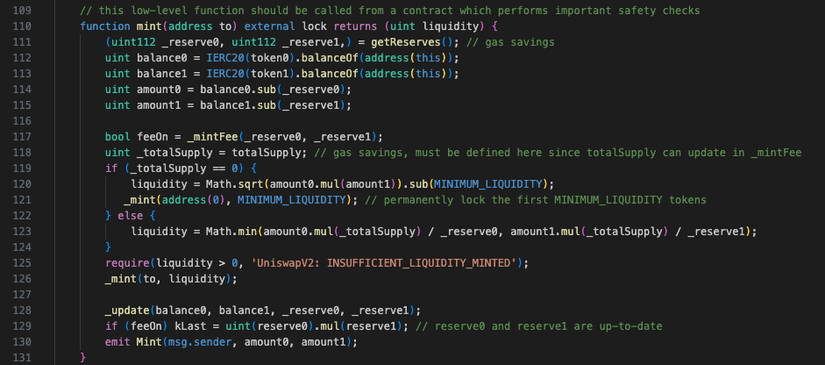
Nếu là provider đầu tiên thêm thanh khoản thì $L$ sẽ được tính theo công thức $L =\sqrt{x * y}$, dòng 119-120.

Những provider tiếp theo chỉ cần tính theo công thức $L_0 = min(\frac{x_0}{x} * L_{total}, \frac{y_0}{y} * L_{total})$ (dòng 122, 123) là sẽ tự động thoả mãn 2 tính chất ở trên. Điều này cho phép những provider này không cần thêm thành khoản đúng tỷ lệ $\frac{x_0}{y_0} = \frac{x}{y}$, với mục đích có thể làm thay đổi price luôn trong lúc thêm thanh khoản, cho nên $L_{0}$ phải là $min(\frac{x_0}{x} * L_{total}, \frac{y_0}{y} * L_{total})$.

2.2. Chuyển đổi từ V2 sang V3

Mặc dụ V2 ko quy ước về công thức giá, nhưng bây giờ chúng ta hãy quy ước rằng P được xem là giá của token0 trên token1, nghĩa là 1 token0 = P token1. Nghĩa là $P = \frac{y}{x}$

Chúng ta có thể biểu diễn tương quan của $x,y,P$ như sau (lưu ý, hình này không đúng về mặt toán học, đừng cố chia tỷ lệ độ dài hay diện tích làm gì, nó chỉ minh hoạ ra cho dễ hiểu):

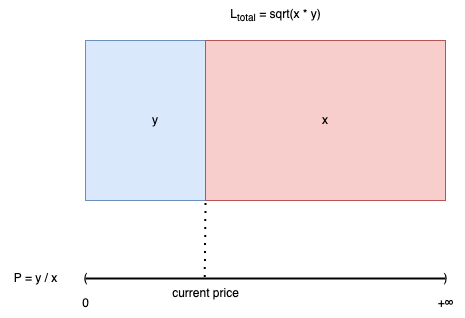
Chúng ta có thể thấy những điều sau với Pool V2:

• $P$ sẽ có khoảng giá trị (price-range) là $(0, +\infin)$, nhưng $P$ sẽ không bao giờ chạm đến 0
• $x$ càng tăng, nghĩa là lượng token0 trong pool càng nhiều thì $P$ càng giảm
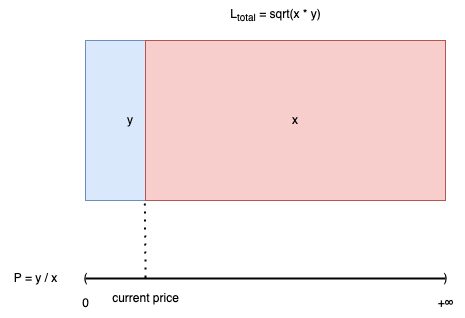
• $y$ càng tăng, nghĩa là lượng token1 trong pool càng nhiều thì $P$ càng tăng
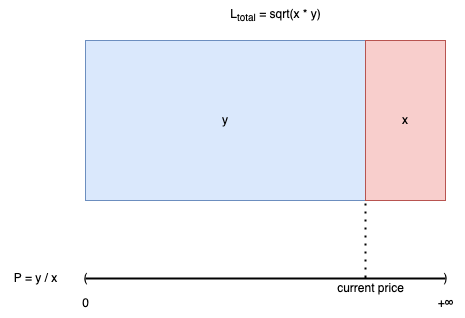
• Bên phải của $P$, chỉ chứa toàn token0. Bên trái của $P$ chỉ chứa toàn token1

Ok, bây giờ hãy qua lại điểm khác nhau về tính năng của V2 và V3 là: thanh khoản khi một provider thêm vào V2, provider không có quyền chọn price-range, $L$ sẽ được hoà tan hoàn toàn vào price-range $(0, +\infin)$. Còn ở V3, provider có quyền chọn price-range cho lượng thanh khoản của mình, khi nào current-price đi vào price-range mà provider đã chọn thì lượng thanh khoản mà anh ấy đã thêm vào mới được phép mang ra sử dụng, và L của mỗi price-range có giá trị khác nhau.

Từ hình mình hoạ của V2, chúng ta có thể mở rộng ra minh hoạ cho V3 như sau: 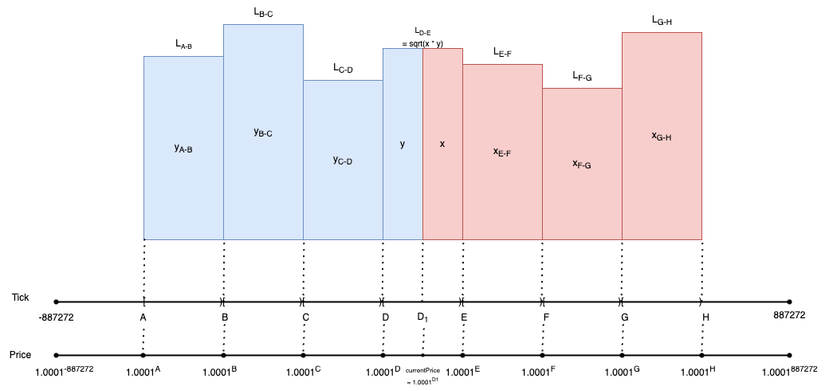Để ra được hình minh hoạ này thì mình tư duy như sau:

• Lấy A,B,C,D,E,F,G,H là những tick mà index của chúng đều chia hết cho tick-spacing, chúng không cần phải cách đều nhau.

• Đầu tiên gom cả PoolV2 thành 1 price-range nhất định, ở đây là D-E. Trong price range này, sẽ có vừa có cả $x$ token0 và $y$ token1, giá hiện tại (current-price) đang là ở điểm D1 thuộc D-E và $L_{D-E} = \sqrt{x * y}$. Và nếu sau khi swap, price không vượt qua khỏi [$1.0001^D$, $1.0001^{E-1}$, thì lệnh swap đó mới được sử dụng token0 hoặc token1 trong thanh khoản $L_{D,E}$

• Bên trái của current-price vẫn sẽ toàn là token1, bên phải của current-price vẫn sẽ toàn là token0.

• Và như mình đã nói ở phần trước, liquidity provider có thể thêm thanh khoản vào bất cứ price-range nào họ muốn. Do đó, L của các đoạn sẽ nhấp nhô (không bằng nhau). Khi họ thêm thanh khoản vào price-range lớn hơn current-price-range, họ chỉ được phép deposit token0. Khi họ thêm thanh khoản vào price-range nhỏ hơn current-price-range, họ chỉ được phép deposit token1.

Nhưng có một vấn đề ở đây là, với các đoạn E-F, F-G, G-H chỉ toàn token0 và các đoạn A-B, B-C, C-D chỉ toàn là token1 thì làm sao xác định được L của mỗi đoạn nếu chỉ dựa vào công thức thuần tuý $L = \sqrt{x * y}$, chẳng phải tất cả L sẽ là 0 sao?

2.3 Hô biến các công thức

Đầu tiên, hãy bắt đầu phân tích từ current-price-range trước:

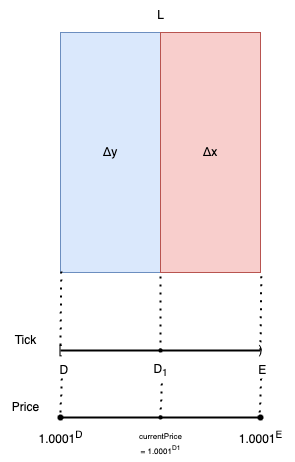
Ví dụ, ban đầu Alice tạo một Pool V3, vẫn chưa có price-range nào có thanh khoản. Bây giờ Alice là người thêm thanh khoản đầu tiên cho Pool, Alice muốn thêm một lượng $L$ thanh khoản vào price-range D-E và sau khi thêm thanh khoản xong, giá P sẽ ở đúng điểm $D1$. Như vậy ta có các tham số đầu vào là:

• L
• $P_{D1}$
• $P_D$ và $P_E$ là 2 cận trên-dưới về gía tương ứng với price-range mà Alice đã chọn.

Chúng ta cần tìm: lượng $\Delta{x}$ token0 và $\Delta{y}$ token1 sao cho $\frac{\Delta{y}}{\Delta{x}}$ rơi đúng điểm $D1$

Ok, đầu tiên, chúng ta có các công thức cơ bản sau:

1. $$L = \sqrt{x * y}$$

2. $$P = \frac{y}{x} <=> \sqrt{P} = \sqrt{\frac{y}{x}}$$

Các công thức tương quan giữa $\Delta{P}$ và $\Delta{x},\Delta{y}$ được suy ra từ công thức 1 và 2 như sau:

3. $$\Delta{y} = L * \Delta{\sqrt{P}}$$

4. $$\Delta{x} = L * \Delta{\frac{1}{\sqrt{P}}}$$

WTF 🤡, clq j z? Tại sao từ 1,2 lại suy ra được 3,4? Chứng minh sao?

Ok chứng minh công thức số 3 trước, đầu tiên mình giả sử trạng thái ban đầu là $x_0, y_0, P_0$, sau một lệnh swap nào đó trạng thái thành $x_1, y_1, P_1$, lưu ý cái giả sử này mình chỉ đang giả sử để chứng minh công thức thôi, đừng thắc mắc sao đang nói về thêm thanh khoản mà lại lôi swap và đây.

$$\Delta{y} = L * \Delta{\sqrt{P}}$$

$$<=> y_1 - y_0 = \sqrt{P_1} - \sqrt{P_0}$$

$$<=>y_1-y_0 = L * (\sqrt{\frac{y_1}{x_1}} - \sqrt{\frac{y_0}{x_0}})$$

Mà như đã nói rất nhiều lần L không thay đổi trong quá trình swap, do đó $L = \sqrt{x_0y_0} = \sqrt{x_1y_1}$. Thay vào L ta có:

$$<=> y_1 - y_0 = \sqrt{\frac{y_1x_1y_1}{x_1}} - \sqrt{\frac{y_0x_0y_0}{x_0}}$$

$$<=> y_1 - y_0 = \sqrt{y_1^2} - \sqrt{y_0^2}$$

$$<=> y_1 - y_0 = y_1 - y_0$$

Chứng minh công thức 4:

$$\Delta{x} = L * \Delta{\frac{1}{\sqrt{P}}}$$

$$x_1 - x_0 = L * (\frac{1}{\sqrt{P_1}} - \frac{1}{\sqrt{P_0}})$$

$$<=> x_1 - x_0 = L * (\frac{1}{\sqrt{\frac{y_1}{x_1}}} - \frac{1}{\sqrt{\frac{y_0}{x_0}}})$$

$$<=> x_1 - x_0 = L * (\sqrt{\frac{x_1}{y_1}}- \sqrt{\frac{x_0}{y_0}})$$

$$<=> x_1 - x_0 = \sqrt{\frac{x_1x_1y_1}{y_1}} - \sqrt{\frac{x_0x_0y_0}{y_0}}$$

$$<=> x_1 - x_0 = \sqrt{x_1^2} - \sqrt{x_0^2}$$

$$<=> x_1 - x_0 = x_1 - x_0$$

Công thức đã có, bây giờ hãy áp dụng nó vào việc tính lượng $\Delta{x}$ token0 và $\Delta{y}$ token1 của việc Alice thêm thanh khoản ở trên:

$$\Delta{x} = L * (\frac{1}{\sqrt{P_{D1}}} - \frac{1}{\sqrt{P_{E}}}) = L * (\frac{\sqrt{P_E} - \sqrt{P_{D1}}}{\sqrt{P_{D1}}\sqrt{P_E}})$$

$$=> \Delta{x} = L * (\frac{\sqrt{1.0001^E} - \sqrt{1.0001^{D1}}}{\sqrt{1.0001^{D1}}\sqrt{1.0001^E}})$$

$$\Delta{y} = L * (\sqrt{P_{D1}} - \sqrt{P_{D}})$$

$$=> \Delta{y} = L * (\sqrt{1.0001^{D1}} - \sqrt{1.0001^{D}})$$

Chắc đang cấn chỗ xác định $P_0, P_1$ cho việc tính $\Delta{x}$ đang hơi ngược với xác định $P_0, P_1$ cho việc tính $\Delta{y}$ đang hơi ngược nhau đúng hông, mường tượng cho dễ thì việc di chuyển giá từ $P_0$ đến $P_1$ sẽ là xu hướng phình to của $\Delta{x}$ hoặc $\Delta{y}$. Do đó:

• Đối với tính $\Delta{x}$ thì $P_0 =P_E$ và $P_1= P_{D1}$
• Đối với tinh $\Delta{y}$ thì $P_0 = P_D$ và $P_1 = P_{D1}$

Ok, đây là khi Alice là người thêm thanh khoản đầu tiên và thiết lập current-price-range, chúng ta sẽ sử dụng cả 2 công thức $(3),(4)$ để tính lượng $\Delta{x}, \Delta{y}$ mà Alice phải cho vào Pool. Còn nếu Bob muốn thêm thanh khoản vào price-range lớn hơn current-price-range và Carol muốn thêm thanh khoản vào price-range nhỏ hơn current-price-range thì sao

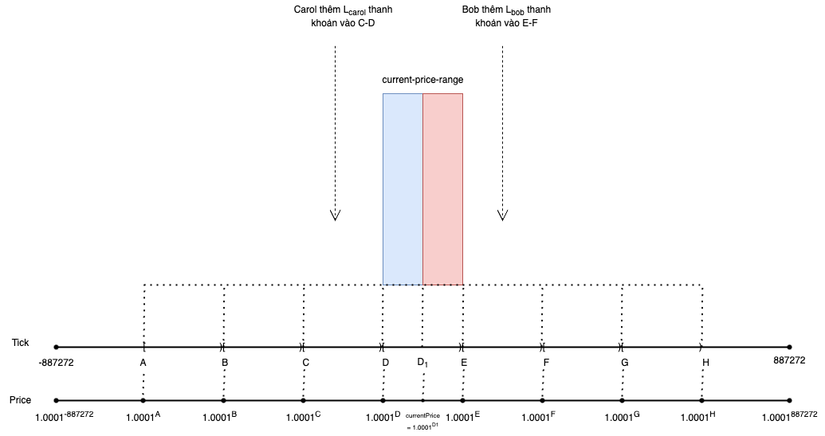
• Vì price-range E-F lớn hơn current-price-range nên nó chỉ chứa token0, do đó, chúng ta chỉ cần sử dụng công thức $(4)$ để tính lượng token0 mà Bob phải cho vào:

$$\Delta{x}_{bob} = L_{bob} * (\frac{1}{\sqrt{P_E}} - \frac{1}{\sqrt{P_F}}) = L_{bob} * (\frac{1}{\sqrt{1.0001^E}} - \frac{1}{\sqrt{1.0001^F}})$$

• Vì price-range C-D nhỏ hơn current-price-range nên nó chỉ chứa token1, do đó, chúng ta chỉ cần sử dụng công thức $(3)$ để tính lượng token1 mà Carol phải cho vào:

$$\Delta{y}_{carol} = L_{carol} * (\sqrt{P_D} - \sqrt{P_C}) = L_{carol} * (\sqrt{1.0001^D} - \sqrt{1.0001^C})$$

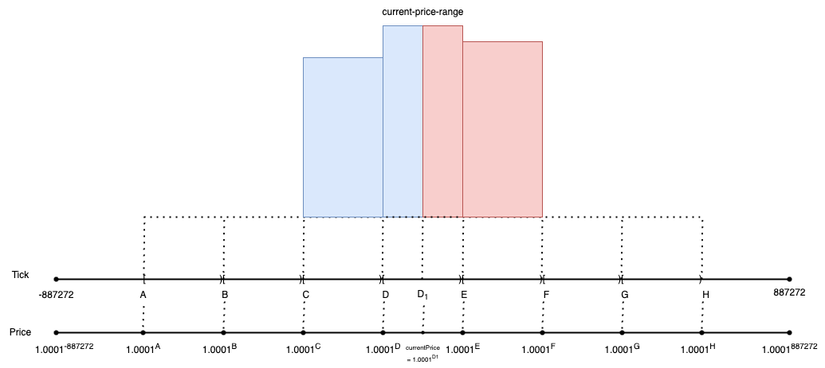
Đối với các price-range còn lại là A-B, B-C và F-G, G-H cũng sử dụng cách tương tự

2.4 Nhìn vào code.

Thật ra có một luồng thoáng hơn ở chỗ Alice tạo pool, xác định current-price ở trên là không cần thiết Alice phải thêm thanh khoản, Alice có thể chỉ tạo pool và xác định current-price, các hành động thêm thanh thanh khoản về sau sẽ tự xác định price-range đang muốn thêm vào có phải là current-price-range hay không mà sử dụng đồng thời công thức $(3), (4)$ hay chỉ sử dụng một trong hai công thức đó.

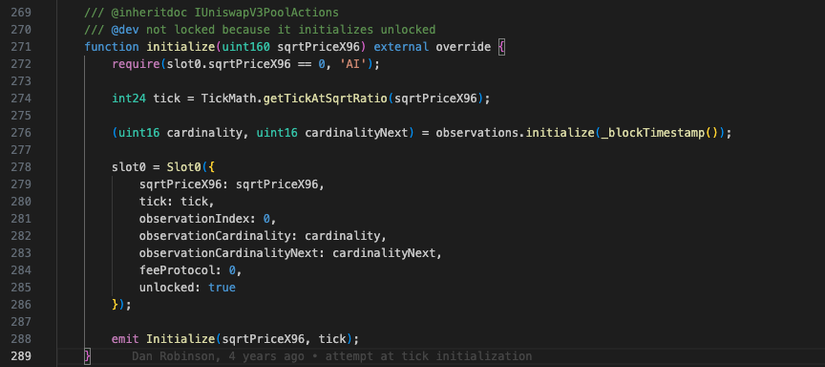
• Tạo Pool, xác định current-price là hàm initialize() của UniswapV3Pool.sol
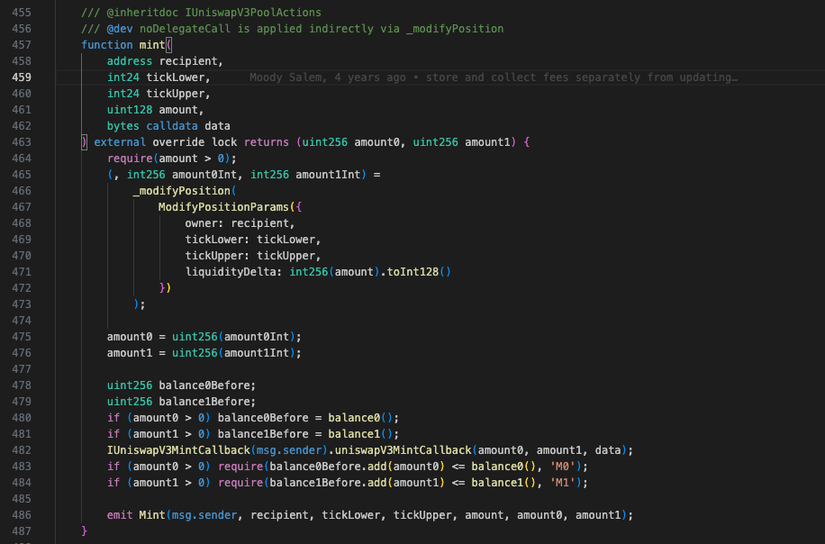
• Thêm thanh khoản là mint() của UniswapV3Pool.sol
• Xác định price-range đang muốn thêm thanh khoản có phải là current-price-range không, hay lớn hơn hay nhỏ hơn và sử dụng công thức tương ứng từ dòng 328 đến 369 của UniswapV3Pool.sol
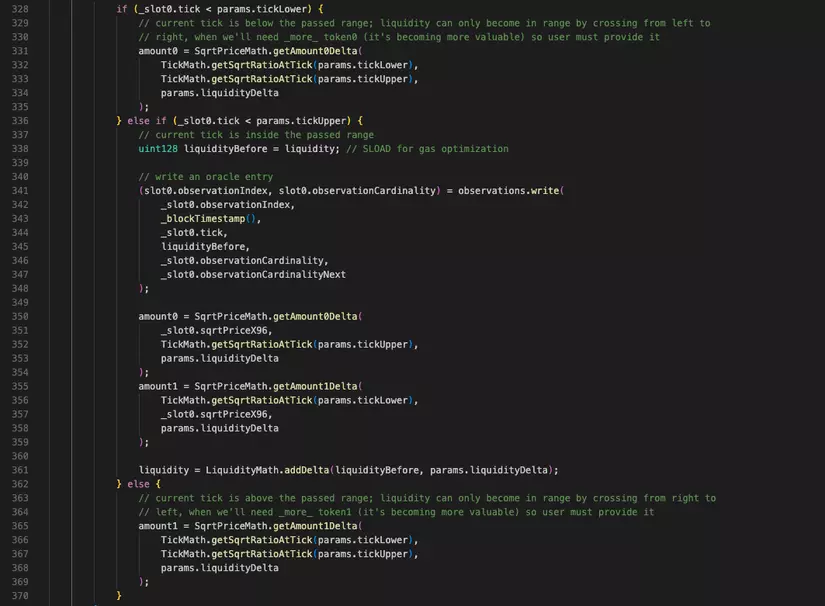
• Nếu lớn hơn current-price-range, chỉ sử dụng công thức $(4)$, từ dòng 328 đến 335
• Nếu là current-price-range, sử dụng cả 2 công thức $(3), (4)$ từ dòng 336 đến 361
• Nếu nhỏ hơn current-price, chỉ sử dụng công thức $(3)$, từ dòng 362 đến 370
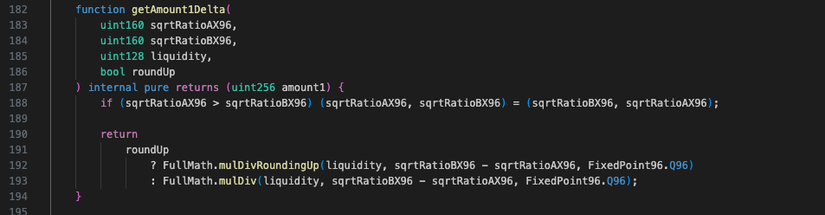
• Code của công thức $(3)$ nằm trong hàm getAmount1Delta() của file libraries/SqrtPriceMath.sol
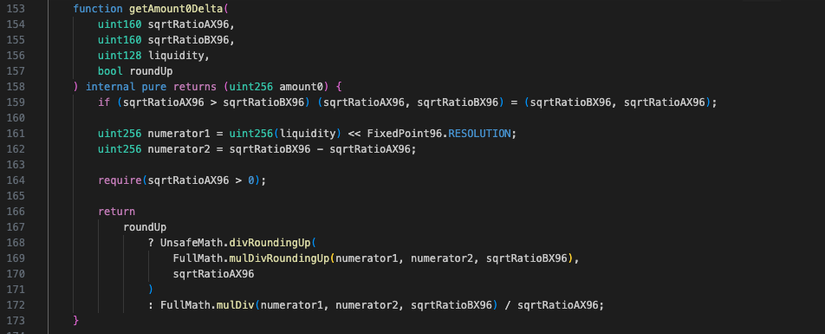
• Code của công thức $(4)$ nằm trong hàm getAmount0Delta() của file libraries/SqrtPriceMath.sol

Xong phần 2, phần 3 mình swap ha!