Giải thuật gióng hàng Needleman-Wunsch.
Bài đăng này đã không được cập nhật trong 6 năm
Sắp xếp thẳng hàng trình tự ( sequence alignment) là phương pháp sắp xếp hai hoặc nhiều trình tự nhằm đạt được sự giống nhau tối đa. Các trình tự này có thể được xen bằng các khoảng trống (thường được diễn tả bằng các gạch nối ngang) tại các vị trí có thể để làm sao tạo thành các cột giống nhau (identical) hoặc tương tự nhau (similar).
tcctctgcctctgccatcat---caaccccaaagt
|||| ||| ||||| ||||| ||||||||||||
tcctgtgcatctgcaatcatgggcaaccccaaagt
Thuật toán quy hoạch động được sử dụng cho bài toán căn chỉnh, gióng hàng tối ưu giữa hai trình tự. Thuật toán tìm kiếm sự liên kết bằng cách đưa ra một ma trận chấm điểm. Bằng cách tìm điểm số cao nhất trong ma trận, từ đó có thể thu được một cách căn chỉnh, gióng hàng hai trình tự.
Thuật toán Needleman-Wunsch là một thuật toán căn chỉnh trình tự, được sử dụng trong tin sinh học để sắp xếp các chuỗi protein hoặc nucleotide. Đó là một trong những ứng dụng đầu tiên của lập trình động để so sánh các trình tự sinh học. Thuật toán được phát triển bởi Saul B. Needman và Christian D. Wunsch và được công bố vào năm 1970.
Thuật toán về cơ bản phân chia một vấn đề lớn (ví dụ: toàn bộ chuỗi) thành một chuỗi các vấn đề nhỏ hơn và nó sử dụng các giải pháp cho các vấn đề nhỏ hơn để tìm ra giải pháp tối ưu cho vấn đề lớn hơn.
Thuật toán Needleman-Wunsch vẫn được sử dụng rộng rãi để căn chỉnh toàn cục (global alignment), đặc biệt khi chất lượng của liên kết toàn cầu là quan trọng nhất. Thuật toán gán điểm cho mọi căn chỉnh có thể và mục đích của thuật toán là tìm tất cả các sắp xếp có thể có điểm cao nhất
Căn chỉnh toàn cục (Global alignment): là một phương pháp trong đó toàn bộ ký tự trên hai trình tự tham gia vào quá trình sắp xếp. Phương pháp này thường được áp dụng để tìm các trình tự tương cận gần.
Căn chỉnh cục bộ (Local alignment): là phương pháp nhằm tìm kiếm các vùng có quan hệ bên trong các chuỗi - hay nói cách khác là chúng có chứa một tập con các ký tự bên trong chuỗi.
Thuật toán Needleman-Wunsch
Thuật toán này có thể được sử dụng cho việc căn chỉnh hai chuỗi hay hai trình tự bất kỳ. Ví dụ hai chuỗi DNA như:
GCATGCU
GATTACA
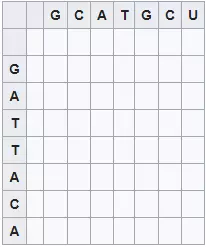
Xây dựng ma trận tính điểm
Dựng ma trận như hình dưới, hàng trên cùng và cột bên trái là hai chuỗi cần căn chỉnh.
Chọn 1 hệ thống tính điểm
Các cặp chữ cái có thể khớp nhau, khác nhau, hoặc có thể được ghép với một khoảng trống - gap (một phần tử được thêm hay bị xóa khỏi một chuỗi)
- Khớp (Match): Hai chữ cái ở chỉ mục hiện tại giống nhau.
- Không phù hợp (Mismatch): Hai chữ cái ở chỉ mục hiện tại là khác nhau.
- Indel (INserts hoặc DELetion): Căn chỉnh tốt nhất liên quan đến một chữ cái thẳng hàng với một khoảng trống (gap) trong chuỗi khác.
Tiếp theo, quyết định làm thế nào để tính điểm từng cặp chữ cái riêng lẻ. Sử dụng ví dụ trên, một cách tính điểm cho việc căn chỉnh có thể là:
Match: +1
Mismatch hoặc Indel: −1
Có ít nhất 3 move như sau: ghép 1-1, ghép 0-1. ghép 1-0. Ngoài ra, trong một số bài toán khác, có thể có ghép 1-2, 2-1, 2-2, ...
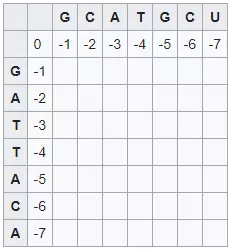
Điền số vào ma trận
Bắt đầu bằng số 0 ở hàng thứ hai, cột thứ hai. Di chuyển qua các ô theo từng hàng, tính điểm cho từng ô. Điểm số được tính bằng cách so sánh điểm của các ô lân cận bên trái, trên cùng hoặc trên cùng bên trái (đường chéo) của ô và thêm điểm thích hợp cho khớp, không khớp hoặc không khớp. Tính điểm số của mỗi cặp trong ba khả năng:
- Đường dẫn từ ô trên cùng hoặc bên trái thể hiện một cặp indel, vì vậy hãy lấy điểm của ô bên trái và ô trên cùng, và thêm điểm cho indel cho mỗi trong số chúng.
- Đường chéo biểu thị một kết quả khớp / không khớp, vì vậy hãy lấy điểm của ô chéo trên cùng bên trái và thêm điểm cho khớp nếu các cơ sở (chữ cái) tương ứng trong hàng và cột khớp với nhau hoặc điểm cho không khớp nếu chúng không khớp.
Điểm kết quả cho ô là lấy max của 3 giá trị trên
Do không có ô 'trên cùng' hoặc 'trên cùng bên trái' cho hàng thứ hai, chỉ có thể sử dụng ô hiện có ở bên trái để tính điểm của từng ô. Do đó -1 được thêm cho mỗi ca sang phải vì điều này thể hiện không thể xóa được từ điểm trước đó. Điều này dẫn đến hàng đầu tiên là 0, -1, -2, -3, -4, -5, -6, -7. Điều tương tự áp dụng cho cột thứ hai vì chỉ có thể sử dụng điểm số hiện có trên mỗi ô.
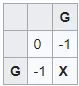
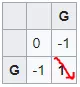
Trường hợp đầu tiên với điểm số hiện có ở cả 3 hướng là giao điểm của các chữ cái đầu tiên (trong trường hợp này là G và G):
- G và G là một cặp khớp nên điểm đường chéo (1-1) là: 0 + match = 0 + 1 = 1
- Điểm Indel từ trái sang (0-1) là: -1 + indel = -1 + (-1) = -2.
- Điểm Indel từ trên xuống (1-0) là: -1 + indel = -1 + (-1) = -2.
Max(1, -2, -2) = 1. X có giá trị là 1.
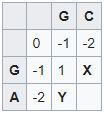
Tương tự với trường hợp dưới:
X:
- Top: (-2)+(-1) = (-3)
- Left: (+1)+(-1) = (0)
- Top-Left: (-1)+(-1) = (-2)
Y:
- Top: (1)+(-1) = (0)
- Left: (-2)+(-1) = (-3)
- Top-Left: (-1)+(-1) = (-2)
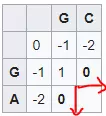
Kết quả như sau:
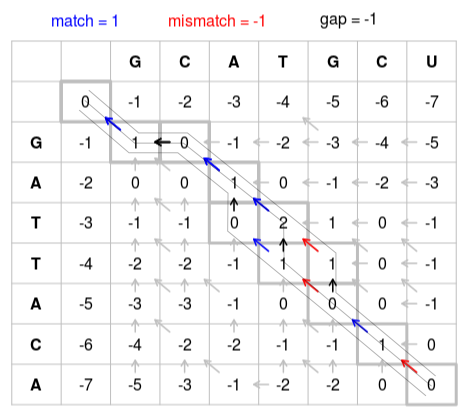
Bước quay lui
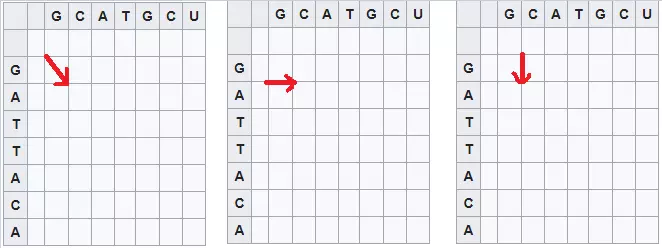
Đánh dấu một đường dẫn từ ô ở phía dưới bên phải trở lại ô ở phía trên bên trái bằng cách làm theo hướng mũi tên. Từ đường dẫn này, chuỗi được xây dựng theo các quy tắc sau:
- Một mũi tên chéo đại diện cho một cặp khớp hoặc không khớp, vì vậy chữ cái của cột và chữ cái của hàng của ô gốc sẽ căn chỉnh.
- Một mũi tên ngang hoặc dọc đại diện cho một indel. Mũi tên ngang sẽ căn chỉnh một khoảng trống ("-") với chữ cái của hàng, mũi tên dọc sẽ căn chỉnh một khoảng cách với chữ cái của cột
- Nếu có nhiều mũi tên để lựa chọn (khi lấy có 2 hoặc cả 3 giá trị bằng nhau khi lấy max), chúng đại diện cho một nhánh của sự sắp xếp. Nếu hai hoặc nhiều nhánh đều thuộc về các đường dẫn từ dưới cùng bên trái đến ô trên cùng bên phải, thì chúng là các sắp xếp khả thi như nhau. Trong trường hợp này, lưu ý các đường dẫn như các ứng cử viên liên kết riêng biệt..
Results:
Sequences Best alignments
--------- ----------------------
GCATGCU GCATG-CU GCA-TGCU GCAT-GCU
GATTACA G-ATTACA G-ATTACA G-ATTACA
Python implementation
Chúng ta sẽ xây dựng ma trận tính điểm, đồng thời cũng xây dựng một ma trận để đánh dẫu đường đi.
Độ phức tạp thuật toán: O(mn)
import numpy as np
from string import *
#-------------------------------------------------------
#This function returns to values for cae of match or mismatch
def Diagonal(n1,n2,pt):
if(n1 == n2):
return pt['MATCH']
else:
return pt['MISMATCH']
#------------------------------------------------------------
#This function gets the optional elements of the aligment matrix and returns the elements for the pointers matrix.
def Pointers(di,ho,ve):
pointer = max(di,ho,ve) #based on python default maximum(return the first element).
if(di == pointer):
return 'D'
elif(ho == pointer):
return 'H'
else:
return 'V'
#--------------------------------------------------------
#This function creates the aligment and pointers matrices
def NW(s1,s2,match = 1,mismatch = -1, gap = -2):
penalty = {'MATCH': match, 'MISMATCH': mismatch, 'GAP': gap} #A dictionary for all the penalty valuse.
n = len(s1) + 1 #The dimension of the matrix columns.
m = len(s2) + 1 #The dimension of the matrix rows.
al_mat = np.zeros((m,n),dtype = int) #Initializes the alighment matrix with zeros.
p_mat = np.zeros((m,n),dtype = str) #Initializes the alighment matrix with zeros.
#Scans all the first rows element in the matrix and fill it with "gap penalty"
for i in range(m):
al_mat[i][0] = penalty['GAP'] * i
p_mat[i][0] = 'V'
#Scans all the first columns element in the matrix and fill it with "gap penalty"
for j in range (n):
al_mat[0][j] = penalty['GAP'] * j
p_mat [0][j] = 'H'
#Fill the matrix with the correct values.
p_mat [0][0] = 0 #Return the first element of the pointer matrix back to 0.
for i in range(1,m):
for j in range(1,n):
di = al_mat[i-1][j-1] + Diagonal(s1[j-1],s2[i-1],penalty) #The value for match/mismatch - diagonal.
ho = al_mat[i][j-1] + penalty['GAP'] #The value for gap - horizontal.(from the left cell)
ve = al_mat[i-1][j] + penalty['GAP'] #The value for gap - vertical.(from the upper cell)
al_mat[i][j] = max(di,ho,ve) #Fill the matrix with the maximal value.(based on the python default maximum)
p_mat[i][j] = Pointers(di,ho,ve)
print np.matrix(al_mat)
print np.matrix(p_mat)
Tham khảo:
https://en.wikipedia.org/wiki/Needleman–Wunsch_algorithm https://en.wikipedia.org/wiki/Sequence_alignment
All rights reserved