Giải quyết deadlock cho hệ thống phân tán bằng những thuật toán phổ biến

Giải quyết deadlock cho hệ thống bằng những thuật toán phổ biến:

Dưới đây là một số phương pháp và công nghệ phổ biến được sử dụng:

Thuật toán bầu chọn (voting algorithm) và Thuật toán gắn nhãn thời gian (time stamping algorithm) là hai phương pháp thường được sử dụng để giải quyết vấn đề deadlock trong hệ thống phân tán. Tuy nhiên, mỗi thuật toán có cách tiếp cận và cơ chế hoạt động khác nhau. Dưới đây là mô tả về cả hai thuật toán:

1. Bầu chọn (Voting algorithm):

Ý tưởng: Thuật toán bầu chọn được sử dụng để chọn ra một tiến trình để giải quyết deadlock trong hệ thống phân tán.

Cơ chế hoạt động:

Mỗi tiến trình gửi thông điệp yêu cầu giải quyết deadlock đến các tiến trình khác.
Tiến trình nhận thông điệp đếm số lượng thông điệp yêu cầu deadlock đã nhận.
Nếu một tiến trình nhận được tất cả các thông điệp yêu cầu deadlock, nó trở thành tiến trình chủ động giải quyết deadlock.
Tiến trình chủ động sẽ giải quyết deadlock bằng cách xóa một hoặc nhiều tiến trình khác để giải phóng tài nguyên.

Khi tiến trình điều phối gặp lỗi thì sẽ phải có quá trình bầu chọn để chọn ra một tiến trình khác làm điều phối thay cho nó. 
Có hai giải thuật bầu chọn hay được sử dụng là:
o Giải thuật áp đảo (Bully Algorithm)
o Giải thuật vòng (Ring Algorithm)

1.1 Bầu chọn áp đảo:

Giả sử:

Mỗi một tiến trình đều có một ID duy nhất.
Tất cả các tiến trình khác đều có thể biết được số ID và địa chỉ của mỗi tiến trình trong hệ thống.
Chọn một tiến trình có ID cao nhất làm khóa.
Tiến trình sẽ khởi động việc bầu chọn nếu như nó khôi phục lại sau quá trình xảy ra lỗi hoặc tiến trình điều phối bị trục trặc.

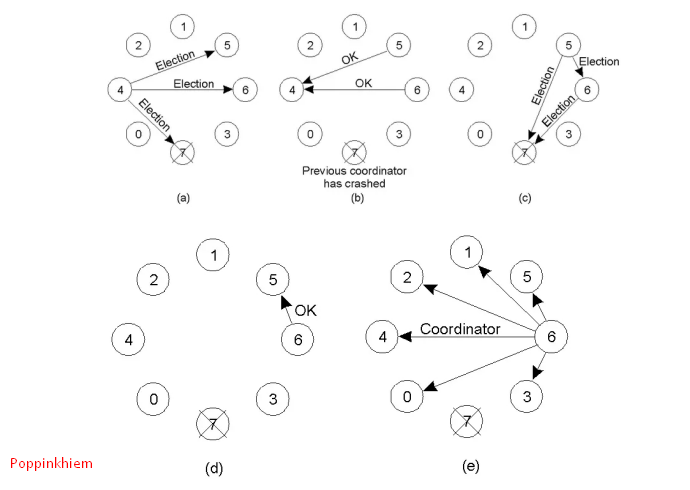
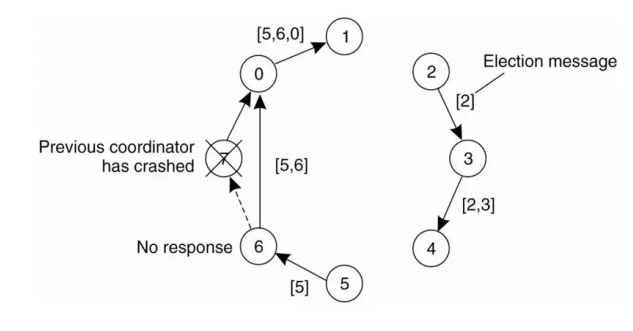
1.2 Giải thuật vòng

Các bước của giải thuật:

Một tiến trình bắt đầu gửi thông điệp Election tới các nút còn tồn tại gần nhất, quá trình gửi theo 1 hướng nhất định.
Nó sẽ thăm dò liên tiếp trên vòng cho đến khi tìm được 1 nút còn tồn tại.
Mỗi một tiến trình sẽ gắn ID của mình vào thông điệp gửi.
Cuối cùng sẽ chọn ra 1 tiến trình có ID cao nhất trong số các tiến trình còn hoạt động và gửi thông điệp điều phối cho tiến trình đó.

2. Thuật toán gắn nhãn thời gian Lamport:

Gắn nhãn thời gian (Time stamping) là một thuật toán được sử dụng để gắn nhãn một thời điểm cụ thể vào một sự kiện, một giao dịch hoặc một thông tin nào đó. Mục đích của việc gắn nhãn thời gian là cung cấp thông tin về thời gian xảy ra sự kiện hoặc tạo ra một chứng cứ thời gian.

Dưới đây là mô tả cơ bản về thuật toán gắn nhãn thời gian:

Lấy thời gian hiện tại: Sử dụng các công cụ và hàm thích hợp trong ngôn ngữ lập trình hoặc hệ điều hành để lấy thời gian hiện tại. Thời gian này có thể được biểu diễn dưới dạng dấu thời gian Unix (epoch time) hoặc định dạng ngày giờ khác.
Định dạng thời gian: Chuyển đổi thời gian lấy được thành định dạng thời gian phù hợp, ví dụ: định dạng ngày giờ ISO 8601.
Gắn nhãn thời gian: Gắn nhãn thời gian vào sự kiện, giao dịch hoặc thông tin cần được gắn nhãn. Điều này có thể được thực hiện bằng cách thêm một trường thời gian vào dữ liệu hoặc sử dụng một phương pháp khác tương thích với ngữ cảnh sử dụng.
Lưu trữ và xử lý: Dữ liệu đã được gắn nhãn thời gian có thể được lưu trữ trong cơ sở dữ liệu, tệp tin, gửi đi qua mạng hoặc xử lý bởi các thuật toán và ứng dụng khác để phục vụ mục đích nào đó.

Quá trình gắn nhãn thời gian cho phép theo dõi, phân tích và xử lý các sự kiện theo thời gian, từ việc xác định thứ tự xảy ra của chúng cho đến việc tính toán khoảng thời gian giữa các sự kiện. Điều này có thể hữu ích trong nhiều lĩnh vực, bao gồm hệ thống giao dịch tài chính, ghi log hệ thống, theo dõi sự kiện trong mạng, và nhiều ứng dụng khác.

Xét định nghĩa mối quan hệ “xảy ra trước” (→)

Khi có a→ b :  a xảy ra trước b thì tất cả các tiến trình trong hệ phân tán thỏa thuận sự kiện a
xảy ra trước rồi đến sự kiện b. Trong đó a và b là hai sự kiện của cùng một tiến trình.
Nếu a xảy ra trước b thì a→b là đúng.
Nếu a là sự kiện bản tin được gửi bởi một tiến trình nào đó và b là sự kiện bản tin
đó được nhận bởi một tiến trình khác thì quan hệ a→ b là đúng.
Quan hệ xảy ra trước có tính bắc cầu: a→ b, b→c thì a→c.

Trên đây là 2 thuật toán tôi đã nêu, ngoài ra còn giải thuật Vector, giải thuật Christian ...được áp dụng rộng rãi trong việc xử lý các hệ thống phân tán. Khi có thời gian tôi sẽ tiếp tục ngâm cứu series này. Chúc các bạn vui vẻ.

Author: PoppinKhiem

DB::transaction distributed transaction transaction