Giải bài toán tìm đường đi ngắn nhất bằng giải thuật Bellman-Ford với code Ruby

Giải thuật Dijkstra như mình đã giới thiệu lần trước có thể giải quyết rất nhanh bài toán tìm đường đi ngắn nhất với đồ thị trọng số dương. (Các bạn có thể xem bài viết về giải thuật Dijkstra tại đây .

Tuy nhiên, với đồ thị trọng số âm, chúng ta sẽ chọn giải thuật Bellman-Ford. Vậy trong bài viết này mình sẽ làm 2 điều:

• Giới thiệu cách giải bài toán shortest-path bằng giải thuật Bellman-Ford
• Thiết kế giải thuật này bằng code ruby.

1. Cách thuật toán Bellman-Ford hoạt động.

Về bài toán tìm đường đi ngắn nhất, các bạn có thể xem đề bài ở trong bài viết trước.

Ý tưởng của thuật toán như sau:

• Ta thực hiện duyệt n lần, với n là số đỉnh của đồ thị.
• Với mỗi lần duyệt, ta tìm tất cả các cạnh mà đường đi qua cạnh đó sẽ rút ngắn đường đi ngắn nhất từ đỉnh gốc tới một đỉnh khác.
• Ở lần duyệt thứ n, nếu còn bất kỳ cạnh nào có thể rút ngắn đường đi, điều đó chứng tỏ đồ thị có chu trình âm, và ta kết thúc thuật toán.

Thuật toán Bellman-Ford có 3 bước:

• Bước 1: Khởi tạo đồ thị

Giải thích bằng pseudocode:

for each v in danh_sách_đỉnh:
       if v is nguồn then khoảng_cách(v):= 0
       else khoảng_cách(v):= vô cùng
       đỉnh_liền_trước(v):= null

• Bước 2: Cập nhật các cạnh với n vòng lặp(n là số node) sao cho đường đi từ source node đến node bị lặp là lớn nhất .

Giải thích bằng pseudocode:

for i from 1 to size(danh_sách_đỉnh)-1:       
       for each (u,v) in danh_sách_cung:
           if khoảng_cách(v) > khoảng_cách(u) + trọng_số(u,v):
               khoảng_cách(v):= khoảng_cách(u) + trọng_số(u,v)
               đỉnh_liền_trước(v):= u

• Bước 3: Kiểm tra xem đồ thị có chu trình âm hay không?

for each (u,v) in danh_sách_cung:
       if khoảng_cách(v) > khoảng_cách(u) + trọng_số(u,v):
           error "Đồ thị chứa chu trình âm"

2. Giải bài toán cụ thể

Giả sử mình có đồ thị trọng số như sau:

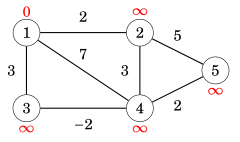
Ta sẽ đi tìm đường đi ngắn nhất từ node 1 đến các node còn lại .

Bước 1: Ta khởi tạo đồ thị với khoảng cách từ node 1 đến chính nó là 0, còn lại là infinity

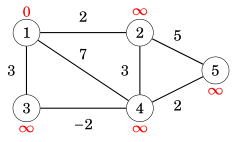
Bước 2: Thực hiện 4 vòng lặp .

Ở vòng lặp đầu tiên, ta cập nhật được đường đi ngắn nhất thông qua các cạnh (1, 2); (1, 3); (1, 4):

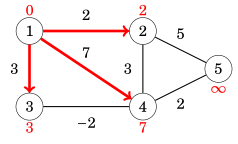
Ở vòng lặp số 2, cạnh (2, 5) và (3, 4) là các cạnh tối ưu:

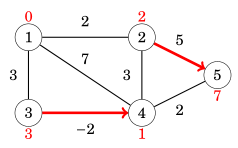
Ở vòng lặp số 3, ta chỉ thấy có cạnh (4,5) cải thiện đường đi từ 1 -> 5 :

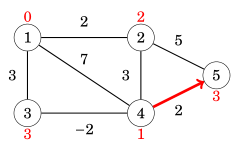
Ở vòng lặp số 4, ta nhận thấy không còn cạnh nào có thể tối ưu được đường đi từ node 1 nữa, vậy nên đồ thị này sẽ không có chu trình âm. Suy ra ta có thể kết thúc thuật toán tại đây.

Và kết quả ta có được là các shortest path từ node 1 như sau:

• Từ 1 đến 2: 1 -> 2
• Từ 1 đến 3: 1 -> 3
• Từ 1 đến 4: 1 -> 3 -> 4
• Từ 1 đến 5: 1 -> 3 -> 4 ->5

3. Thiết kế giải thuật bằng code ruby

Đầu tiên, mình sẽ tạo 1 class để khởi tạo các đối tượng node:

class Node
  attr_accessor :name, :graph

  def initialize(name)
    @name = name
  end
end

Và 1 class để khởi tạo các cạnh.

class Edge
  attr_accessor :from, :to, :weight

  def initialize(from, to, weight)
    @from, @to, @weight = from, to, weight
  end

  def <=>(other)
    self.weight <=> other.weight
  end
end

Mỗi đối tượng cạnh có 3 thuộc tính:

• @from, @to : là 2 node của cạnh .
• @weight : độ dài cạnh

Mình thêm 1 method <=> để có thể so sánh độ dài các cạnh với nhau .

Ta tạo 1 class để khởi tạo đồ thị :

class Graph
  attr_accessor :nodes
  attr_accessor :edges

  def initialize
    @nodes = []
    @edges = []
  end

  def add_node(node)
    nodes << node
    node.graph = self
  end

  def add_edge(from, to, weight)
    edges << Edge.new(from, to, weight)
  end
end

Hai methods add_node và add_class sẽ giúp mình định hình được đồ thị.

Giờ mình sẽ tạo 1 class chính để giải quyết bài toán.

class BellmanFord
  def initialize(graph, source_node)
    @graph = graph
    @source_node = source_node
    @path_to = {}
    @distance_to = {}

    compute_shortest_path
  end

  def shortest_path_to(node)
    path = []
    while node != @source_node
      path.unshift(node)
      node = @path_to[node]
    end

    path.unshift(@source_node).map { |node| node.name }
  end

  private
  def compute_shortest_path
    update_distance_of_all_edges_to(Float::INFINITY)
    @distance_to[@source_node] = 0

    @graph.nodes.size.times do
      @graph.edges.each do |edge|
        relax(edge)
      end
    end
  end

  def update_distance_of_all_edges_to(distance)
    @graph.nodes.each do |node|
      @distance_to[node] = distance
    end
  end

  def relax(edge)
    if @distance_to[edge.to] > @distance_to[edge.from] + edge.weight
      @distance_to[edge.to] = @distance_to[edge.from] + edge.weight
      @path_to[edge.to] = edge.from
    end
  end
end

Khi 1 bài toán được khởi tạo, tương ứng với 1 instance của class BellmanFord, sẽ có 2 tham số tương đương với dữ kiện của bài toán là:

• @graph : là 1 thể hiện của lớp Graph - cũng là đồ thị của bài toán .
• @soure_node : là node đích của bài toán . Ta sẽ tìm đường đi ngắn nhất của các node còn lại đến node này.

Và kết quả của bài toán nằm trong biến @path_to - nó là 1 Hash chứa các node kề mà 1 node nên nối đến để có được đường đi ngắn nhất.

Với bài toán đồ thị như thế này:

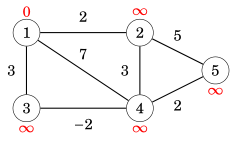
Mình sẽ thử chạy bài toán như sau:

Khởi tạo các node của đồ thị:

@graph = Graph.new
@graph.add_node(@node1 = Node.new("Node #1"))
@graph.add_node(@node2 = Node.new("Node #2"))
@graph.add_node(@node3 = Node.new("Node #3"))
@graph.add_node(@node4 = Node.new("Node #4"))
@graph.add_node(@node5 = Node.new("Node #5"))

Khởi tạo các cạnh cho đồ thị:

 #Các cạnh từ node1
 @graph.add_edge(@node1, @node2, 2)
 @graph.add_edge(@node1, @node3, 3)
 @graph.add_edge(@node1, @node4, 7)
 
 #Các cạnh từ node2
 @graph.add_edge(@node2, @node4, 3)
 @graph.add_edge(@node2, @node5, 5)
 
 #Cạnh từ node3
 @graph.add_edge(@node3, @node4, -2)
 
 #Cạnh từ node4
 @graph.add_edge(@node4, @node5, 2)

Giờ ta sẽ giải bài toán tìm đường đi ngắn nhất từ node1 đến các node còn lại rất đơn giản:

bai_toan_1 = BellmanFord.new(@graph, @node1).shortest_path_to(@node2)
=> ["Node #1", "Node #2"]
bai_toan_2 = BellmanFord.new(@graph, @node1).shortest_path_to(@node3)
=> ["Node #1", "Node #3"]
bai_toan_3 = BellmanFord.new(@graph, @node1).shortest_path_to(@node4)
=> ["Node #1", "Node #3", "Node #4"]
bai_toan_4 = BellmanFord.new(@graph, @node1).shortest_path_to(@node5)
=> ["Node #1", "Node #3", "Node #4", "Node #5"]

---

References:

https://www.geeksforgeeks.org/bellman-ford-algorithm-dp-23/

https://thuytrangcoding.wordpress.com/2018/03/19/graph-shortestpath-bellmanford/