1. Entropy

1.1 Lý thuyết thông tin, entropy

Information Theory - lý thuyết thông tin là một nhánh của toán học liên quan tới đo đạc, định lượng và mã hóa thông tin. Cha đẻ của Information Theory là Claude Shannon. Ông nghiên cứu về cách mã hóa thông tin khi truyền tin, sao cho quá trình truyền tin đạt hiệu quả cao nhất mà không làm mất mát thông tin.

H1: Claude Shannon

Năm 1948, trong một bài viết của mình, Claude Shannon đã nhắc tới khái niệm information entropy như là một độ đo để định lượng lượng thông tin hay độ bất định/không chắc chắn của thông tin. Có nhiều cách dịch entropy: độ bất định, độ hỗn loạn, độ không chắc chắn, độ bất ngờ, độ khó đoán ... của thông tin hay lượng thông tin. Trong bài này, mình sẽ giữ nguyên từ entropy thay vì dịch sang tiếng Việt.

Để dễ hiểu hơn, mình sẽ lấy một ví dụ như sau: giả sử sau những lần quan sát thời tiết trong 1 năm, bạn ghi chép được thông tin như sau:

• Vào mùa đông, xác suất ngày nắng (nhẹ) là 100%, mưa là 0%. Như vậy dựa vào xác suất đó, mùa đông ta hoàn toàn tự tin đoán được ngày mai mưa hay nắng. Trong trường hợp này, độ chắc chắn cao, sáng mai ngủ dậy, trời không có mưa thì ta cũng không thấy bất ngờ, tức thông tin tiếp nhận đó không có nhiều giá trị.
• Vào mùa hè, xác suất một ngày không mưa là 50%, có mưa là 50%. Như vậy xác suất mưa/nắng là như nhau. Ta rất khó đoán xem ngày mai mưa hay nắng, độ chắc chắn là không cao. Nói cách khác, ngày mai có mưa hay nắng đều làm ta bất ngờ hơn trong trường hợp 1.
• Như vậy, ta cần một cơ chế để đo lường sự bất định của thông tin, nói cách khác là đo lượng thông tin.

Qua ví dụ trên, ta đã có cái nhìn rõ hơn về khái niệm entropy.

1.2 Entropy và mã hóa thông tin

1.2.1 Mã hóa thông tin

Để hiểu hơn về khái niệm, tính ứng dụng và cách tính entropy, trước tiên ta dạo qua một lượt về chủ đề mã hóa thông tin.

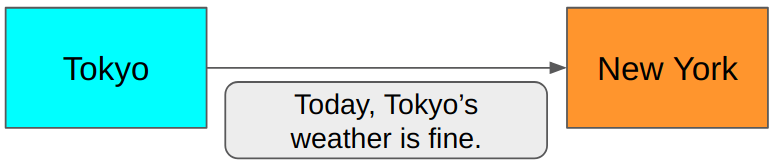
Giả sử khi truyền tin thời tiết từ Tokyo tới New York, với giả sử cả hai bên đều đã biết trước thông gửi đi chỉ là vấn đề mưa/nắng của Tokyo. Ta có thể gửi message "Tokyo, Tokyo's weather is fine" đi. Tuy nhiên, có vẻ cách này hơi dư thừa. Do cả hai điểm cầu Tokyo và New York đều biết rằng thông tin truyền đi/tới đều về thời tiết Tokyo. Nghĩa là điểm Tokyo chỉ cần truyền đi 1 trong 2 tin nhắn mưa-nắng là đủ đề người ở New York hiểu. Cách này nghe qua có vẻ khá hợp lý, tuy nhiên vẫn chưa tối ưu. Hai bên chỉ cần quy ước trước với nhau rằng: mưa là 0, nắng là 1. Như vậy giá trị truyền đi chỉ cần (0, 1) là đủ. Theo cách này, thông tin truyền đi đã được tối ưu mà không sợ bị mất mát, hiểu nhầm giữa hai bên gửi/nhận. Quy tắc mã hóa mưa-0, nắng-1 gọi là 1 bảng mã hóa.

Với cách mã hóa trên, ta đã dùng tới 1 bit để mã hóa thông tin. Trong hệ nhị phân, 1 bit bất kì có giá trị 0 hoặc 1. Dưới đây là một mô hình mã hóa và truyền dẫn thông tin. Thông tin được mã hóa (theo 1 bảng mã quy ước trước) trước khi truyền đi. Tại điểm nhận, người nhận sẽ nhận được các thông tin đã bị mã hóa, lúc này nơi nhận cần tiến hành giải mã để nhận được thông tin gốc ban đầu.

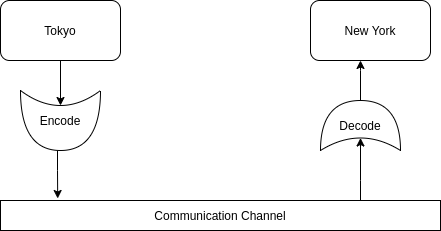
Mô hình mã hóa và truyền dẫn thông tin đơn giản

1.2.2 Entropy

Kích cỡ mã hóa trung bình

Ta đã hiểu được cách mã hóa thông tin. Vậy làm sao để so sánh độ hiểu quả khi mã hóa bằng hai bảng mã khác nhau. Nói cách khác, làm sao để xác định được bảng mã nào tốt hơn. Hãy quan sát hình dưới đây.

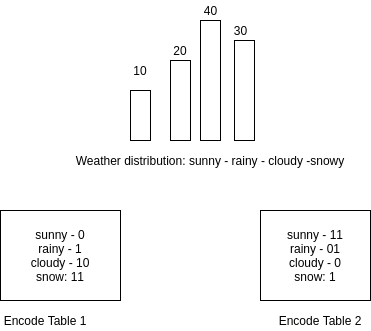
H4. Bảng thống kê tần xuất thời tiết và hai cách mã hóa khác nhau.

Lưu ý: khi mã hóa, các số 0 đừng trước sẽ được lược bỏ, VD: 001 -> 1, 0000100 -> 100 ...

Giả sử, sau 100 lần ghi nhận thời tiết tại Tokyo, người ta thu được phân phối như hình trên với tần xuất nắng-mưa-mây-tuyết lần lượt là 10, 20, 40, 30 lần. Ta có hai bảng mã hóa như trong hình. Để so sánh độ hiểu quả của hai bảng mã trên, ta so sánh số bit trung bình được truyền đi mỗi lần truyền tin.

• Bảng mã 1: everage_bit = $(10 * 1 + 20*1 + 40* 2 + 30*2)/100 = 1.7$ bit.
• Bảng mã 2: everage_bit = $(10* 2 + 20* 2 + 40*1 + 30*1)/100 = 1.1$ bit

Trong lĩnh vực mã hóa, bảng mã 2 được coi là tối ưu hơn, tốt hơn bảng mã 1 vì nếu dùng bảng mã 2 sẽ tiết kiệm được số bit hơn, tốn ít băng thông (khi truyền tin) hay chiếm ít dung lượng (lưu trữ). Cách tính trên được gọi là tính kích cỡ mã hóa trung bình

$$everageBit = p_1*n_1 + p2*n_2 + ... + p_k*n_n$$

$$(1)$$

Với $n_i$ là số bít dùng để mã hóa tín hiệu có tần xuất $p_i$

Kích cỡ mã hóa trung bình tối thiểu

Vậy làm sao để chọn ra cách mã hóa tối ưu nhất. Chúng ta cần chọn ra cách mã hóa có kích cỡ mã hóa trung bình nhỏ nhất.

Vừa rồi là 1 ví dụ đơn giản về chủ đề thời tiết với 4 loại tin nhắn (nắng, mưa, mây, tuyết) cần mã hóa, ta chỉ cần dùng 2 bit là đủ để mã hóa 4 loại tin nhắn này. Tương tự với N kiểu tin nhắn, ta cần số bit mã hóa là:

$$n = \log_2^N$$

Giả sử 1 các tin nhắn này đều có tần suất xuất hiện như nhau là $p=1/N$.

$$n_p = \log_2^N = \log_2^\frac {1} {p}=-\log_2^p$$

Như vậy $-\log_2^{P}$ là số bit tối thiểu để mã hoá 1 tin nhắn với xác suất xuất hiện $p$. Kết hợp với công thức (1), ta được công thức tính kích cỡ mã hóa trung bình tối thiểu, đây chính là công thức tính Entropy:

$$Entropy = -\sum_{i}^{n} p_i * n_i = -\sum_{i}^{n} p_i * \log_2^{p_i}$$

Trong thực tế, ta có thể thay $\log_2$ bằng $\log_{10}$, $\log_e$ ..

Kết luận: entropy cho chúng ta biết kích thước mã hóa trung bình tối thiểu theo lý thuyết cho các sự kiện tuân theo một phân phối xác suất cụ thể.

Tính chất của Entropy.

Với công thức tính entropy ở trên, entropy được tính hoàn toàn dựa vào xác suất. Giả sử với phân phối xác suất về thời tiết (mưa, nắng) là P = {p1, p2}. Người ta nhận ra Entropy(P) đạt max khi p1=p2. Khi p1 và p2 càng lệch nhau thì Entropy(P) càng giảm. Nếu p1=p2=0.5, entropy đạt max, ta rất khó để đoán thời tiết ngày mai mưa hay nắng. Nếu p1=0.1 và p2=0.9, ta sẽ tự tin đoán rằng ngày mai trời sẽ nắng, lúc này entropy có giá trị thấp hơn nhiều.

Entropy cao đồng nghĩa với việc ta khó đoán trước được sự kiện sắp xảy ra. Ta có thể gọi đó là sự bất định, sự bất ổn hay entropy là 1 thước đo sự "khó đoán" của thông tin.

2. Cross Entropy

Như đã mình đã định nghĩa ở trên, entropy là kích thước mã hóa trung bình tối thiểu theo lý thuyết cho các sự kiện tuân theo một phân phối xác suất cụ thể. Miễn là chúng ta biết được phân phối đó, ta sẽ tính được Entropy.

Tuy nhiên, không phải lúc nào ta cũng biết được phân phối đó. Như ví dụ thời tiết trong phần 1, phân phối chúng ta dùng thực chất chỉ là phân phối ta thu được từ việc thống kê chuỗi sự kiện đã xảy ra trong quá khứ. Ta không thể đảm bảo rằng thời tiết trong năm tiếp theo cũng giống hệt năm ngoái. Nói cách khác, các phân phối ta thu được từ việc thống kê trong quá khử chỉ là sấp xỉ, gần đúng của phân phối thực sự của tín hiệu tương lai.

Để dễ hiểu hơn, mình sẽ lấy ví dụ vẫn về thời tiết như sau:

• Đầu năm 2019, người ta thống kê thời tiết cả năm 2018 và thu được phân phối (nắng, mưa, mây, tuyết) là Q = {0.1, 0.3, 0.4, 0.2}
• Người ta dựa vào Q để lập bảng mã hóa 4 tin nhắn này cho năm tới 2019. Q được gọi là phân phối ước lượng. Tin nhắn được mã hóa và vẫn tiếp tục được truyền đi trong cả năm 2019 từ Tokyo tới New York.
• Tới cuối năm 2019, người ta thống kê lại thời tiết cả năm, thu được phân phối mới là P = {0.11, 0.29, 0.41, 0.19}. P được coi là phân phối chính xác đối với năm 2019.

Như vậy, dựa theo công thức đã chứng minh ở phần 1, số bit trung bình được dùng trong cả năm 2019 là:

$$CrossEntropy(P, Q) = -\sum_{i}^{n} p_i * \log_2^{q_i}$$

Như vậy, Entropy của tín hiệu này có phân phối P (tính kì vọng dựa vào P) nhưng lại được mã hóa dựa vào phân phối Q. Đó là lí do cái tên CrossEntropy ra đời (cross có nghĩa là chéo nhau, mình không biết dịch thế nào cho chuẩn).

Tính chất của CrossEntropy đặc biệt ở chỗ:

• đạt giá trị minimum nếu P == Q
• rất nhạy cảm với sự sai khác giữa $p_i$ và $q_i$. Khi $p_i$ và $q_I$ càng khác nhau, giá trị cross_entropy càng tăng nhanh.

Bởi vì các bài toán machine learning thường quy về bài toán xây dựng model sao cho output càng gần target càng tốt (output, target thường đều ở dạng phân phối xác suất). Dựa vào tính nhạy cảm này, người ta dùng CrossEntropy để tối ưu hóa các model.

3. KL Divergence

Sau khi đã đi qua phần Cross Entropy, bạn sẽ thấy KL Divergence rất đơn giản.

Vẫn với ví dụ về thời tiết trong phần 2. Giả sử vào cuối năm 2019, người ta tính được CrossEntropy(P, Q). Lúc này, người ta muốn xác định xem họ đã tốn, tổn thất thêm bao nhiêu bit khi mã hóa dựa vào Q thay vì dùng P. Ta có:

$$D_{KL} (P||Q) = CrossEntropy(P, Q) - Entropy(P)$$

$$= -\sum_{i}^{n} p_i * \log_2^{q_i} + \sum_{i}^{n} p_i * \log_2^{p_i}$$

$$= \sum_{i}^{n} p_i * \log_2^{\frac{p_i}{q_i}}$$

Như vậy, KL Divergence là 1 cách để đó tổn thất khi ước lượng, xấp xỉ 1 phân phối P bằng phân phối Q.

Tính chất DL DIvergence:

• Không có tính đối xứng, tức $D_{KL} (P||Q) \neq D_{KL} (Q||P)$
• Tương tự CrossEntropy, DL cũng rất nhạy cảm với sự sai khác giữa $p_i$ và $q_i$

Trong các bài toán Machine Learning/Deep Learning, do Entropy(P) là không đổi (P là phân phối target -> không đổi) nên tối ưu hàm KL_Divergence cũng tương đương với tối ưu hàm CrossEntropy. Nói các khác, việc bạn dùng KL_Divergence hay CrossEntropy trong Machine Learning là như nhau (trong các lĩnh vực khác thì không).

4. Tham khảo

1. Machine learning summary fundamental - https://jonathan-hui.medium.com

2. KL Divergence Demystified - Medium.com

3. What is Cross-Entropy in Machine learning? - https://medium.com