Disjoint Set Union (DSU - Union Find) - Part 1
Xin chào anh em, lại là tôi - Jim đây!
Dạo gần đây tôi hơi bận nên nay với quay trở lại chém gió cùng anh em sau hơn 1 tháng "gác" bút.
Hôm nay, tôi sẽ chia sẻ với anh em một trong những cấu trúc dữ liệu đơn giản và mạnh mẽ trong bộ công cụ của lập trình viên thi đấu: Disjoint Set Union, hay còn gọi là DSU. Chúng ta sẽ cùng nhau đi từ những khái niệm cơ bản nhất đến các kỹ thuật nâng cao, biến DSU từ một cái tên xa lạ trở thành vũ khí sắc bén của anh em.
Bắt đầu thôi!
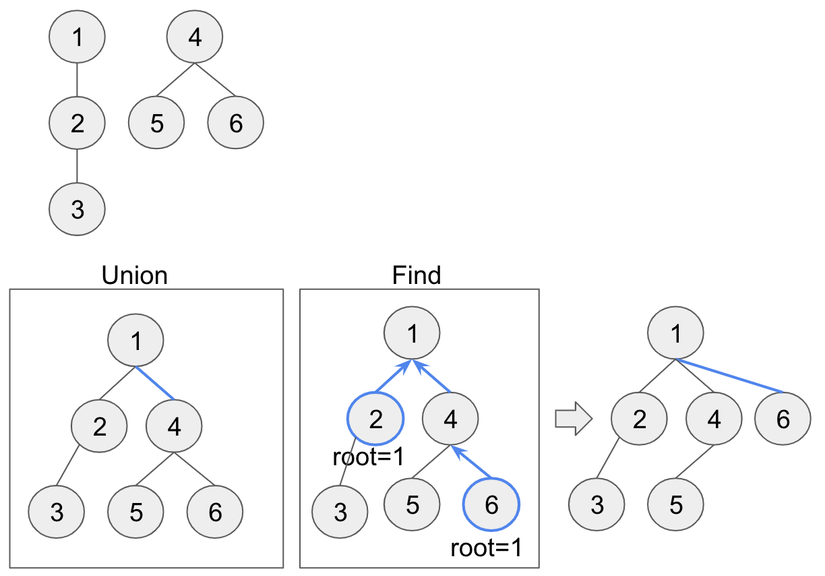
1. DSU là gì?
Tưởng tượng anh em đang xây dựng backend cho một mạng xã hội. Một tính năng cốt lõi là kiểm tra nhanh xem hai người, ví dụ Alice và Bob, có kết nối với nhau hay không, dù là qua một chuỗi bạn chung rất dài. Tình huống này đặt ra hai câu hỏi:
- Kiểm tra kết nối: Liệu Alice và Bob có thuộc cùng một nhóm bạn không?
- Hợp nhất nhóm: Điều gì xảy ra khi hai nhóm bạn riêng biệt hợp nhất, vì một người từ nhóm này kết bạn với một người từ nhóm kia?
Khi có hàng triệu người dùng, việc duyệt đồ thị bằng DFS hay BFS cho mỗi lần kiểm tra sẽ cực kỳ chậm. Chúng ta cần một công cụ chuyên biệt cho bài toán này - một công cụ có thể trả lời các câu hỏi về "thuộc cùng một nhóm" và "hợp nhất các nhóm" một cách hiệu quả nhất.
Cách tiếp cận này đặt khái niệm trừu tượng về các tập hợp rời rạc vào một vấn đề thực tế, mở đường cho DSU như một giải pháp hoàn hảo.
Gặp gỡ DSU
Disjoint Set Union (DSU), hay Union-Find, là cấu trúc dữ liệu chuyên dụng để quản lý các nhóm không giao nhau này. Để dễ hình dung, tôi sẽ dùng một phép so sánh xuyên suốt bài viết:
- Khu Rừng: Toàn bộ người dùng trên mạng xã hội là một khu rừng.
- Những Cái Cây: Mỗi nhóm bạn là một cây trong khu rừng.
- Đại diện (Gốc): Mỗi cây có một gốc (root) hay đại diện (representative) duy nhất để xác định nhóm đó. Nếu biết gốc của cây, anh em sẽ biết mình đang ở nhóm nào.
Cái tên Union-Find mô tả trực tiếp mục đích của cấu trúc này. Không giống như Mảng hay Danh sách liên kết được đặt tên theo cách triển khai, DSU được đặt tên theo bài toán mà nó giải quyết.
Với phép so sánh khu rừng, hai hoạt động chính của DSU trở nên rất trực quan:
- Find(x): "Phần tử x thuộc cây nào?" Thao tác này tìm gốc của cây chứa x. Nếu
Find(Alice)vàFind(Bob)trả về cùng một gốc, họ ở trong cùng một nhóm. - Union(x, y): "Hợp nhất các cây chứa x và y." Thao tác này kết nối hai nhóm bạn riêng biệt thành một.
Về cơ bản, DSU cung cấp một giao diện cực kỳ đơn giản để giải quyết các vấn đề phức tạp về kết nối. Nhiệm vụ của chúng ta bây giờ là tìm cách triển khai người gác rừng này một cách hiệu quả nhất.
2. Xây Dựng DSU:
Bước 1: Cách làm ngây thơ
Hãy bắt đầu với cách tiếp cận đơn giản nhất. Mỗi tập hợp được biểu diễn như một cây, và chúng ta có thể lưu cấu trúc này bằng một mảng parent. Tại chỉ số i, parent[i] lưu nút cha của phần tử i. Ban đầu, mỗi phần tử là gốc của chính nó: parent[i] = i.
- find(i): Để tìm gốc, chúng ta đi ngược lên cây cho đến khi gặp một phần tử là cha của chính nó (
parent[i] == i). - union(i, j): Để hợp nhất hai tập hợp, ta tìm gốc của
i(root_i) và gốc củaj(root_j). Sau đó, cho một gốc làm cha của gốc kia, ví dụparent[root_i] = root_j.
Mã C++ (Ngây thơ):
// Khởi tạo DSU với n phần tử
void makeSet(int n)
{
parent.resize(n);
for (int i = 0; i < n; ++i)
parent[i] = i;
}
// Thao tác Find ngây thơ
int findSet(int v)
{
while (v != parent[v])
v = parent[v];
return v;
}
// Thao tác Union ngây thơ
void unionSets(int a, int b)
{
a = findSet(a);
b = findSet(b);
if (a != b)
parent[b] = a;
}
Vấn đề: Cách này có một lỗ hổng nghiêm trọng. Nếu ta hợp nhất union(1, 2), union(2, 3), union(3, 4), ... cây kết quả sẽ bị suy biến thành một danh sách liên kết. Khi đó, thao tác findSet có thể mất đến , quá chậm cho hàng triệu truy vấn. Khu rừng của chúng ta đã trở nên cong vẹo và khó di chuyển.
Nâng Cấp 1: Nén Đường Đi
Tối ưu hóa đầu tiên và mạnh mẽ nhất là Nén đường đi (Path Compression). Ý tưởng rất đơn giản: một khi đã mất công đi từ nút x lên đến gốc, tại sao không tận dụng thông tin này? Chúng ta có thể cho x (và tất cả các nút trên đường đi) trỏ thẳng đến gốc. Điều này làm phẳng cây một cách đáng kể, giúp các lần tìm kiếm sau này nhanh hơn rất nhiều.
Đây là chiến lược "khắc phục theo yêu cầu": chúng ta không ngăn cây trở nên sâu, mà chủ động làm phẳng nó mỗi khi duyệt qua.
Mã C++ (với Nén Đường Đi): Phiên bản đệ quy của nén đường đi nổi tiếng vì sự tinh tế và ngắn gọn:
// Thao tác Find với tối ưu hóa Nén Đường Đi
int findSet(int v)
{
if (v == parent[v])
return v;
// Gán trực tiếp cha của v là gốc của tập hợp
return parent[v] = findSet(parent[v]);
}
Khi hàm findSet được gọi đệ quy, nó sẽ đi lên đến gốc. Trên đường quay về, phép gán parent[v] = ... được thực thi, cập nhật cha của mỗi nút trên đường đi để trỏ trực tiếp đến gốc. Một thao tác find tốn kém sẽ "trả công" bằng cách dọn đường cho tất cả các thao tác trong tương lai.
Nâng Cấp 2: Hợp Nhất Thông Minh
Nén đường đi rất mạnh, nhưng đó mới là một nửa câu chuyện. Tối ưu hóa thứ hai, Hợp nhất theo Kích thước/Hạng (Union by Size/Rank), là một chiến lược chủ động để ngăn cây phát triển quá sâu ngay từ đầu. Thay vì hợp nhất tùy tiện, chúng ta tuân theo một nguyên tắc đơn giản để giữ cây luôn cân bằng.
Có hai biến thể phổ biến:
- Hợp nhất theo Kích thước (Union by Size): Luôn gắn cây nhỏ hơn vào gốc của cây lớn hơn.
- Hợp nhất theo Hạng (Union by Rank): Luôn gắn cây có hạng (giới hạn trên về chiều cao) thấp hơn vào gốc của cây có hạng cao hơn.
Cả hai phương pháp đều đạt cùng độ phức tạp. Union by Size thường dễ triển khai hơn và còn cung cấp thông tin về kích thước thành phần, rất hữu ích.
Bây giờ, hãy kết hợp cả hai tối ưu hóa để tạo ra một lớp DSU hoàn chỉnh.
Mã C++ (Tối ưu hóa hoàn toàn):
struct DSU
{
vector<int> parent;
vector<int> sz; // sz[i] lưu kích thước của thành phần có gốc là i
// Constructor: Khởi tạo DSU với n phần tử
DSU(int n)
{
parent.resize(n);
// iota điền vào vector với các giá trị tăng dần (0, 1, 2,...)
iota(parent.begin(), parent.end(), 0);
sz.assign(n, 1); // Ban đầu mỗi thành phần có kích thước là 1
}
// Thao tác Find với Nén Đường Đi
int find(int i)
{
if (parent[i] == i)
return i;
return parent[i] = find(parent[i]);
}
// Thao tác Union với Hợp nhất theo Kích thước
void unite(int i, int j)
{
int root_i = find(i);
int root_j = find(j);
if (root_i != root_j)
{
// Gắn cây nhỏ hơn vào gốc của cây lớn hơn
if (sz[root_i] < sz[root_j])
swap(root_i, root_j);
parent[root_j] = root_i;
sz[root_i] += sz[root_j];
}
}
// Hàm tiện ích để lấy kích thước thành phần
int size(int i)
{
return sz[find(i)];
}
};
Hai tối ưu hóa này có mối quan hệ cộng sinh. Union by Size/Rank là biện pháp phòng ngừa, còn Path Compression là biện pháp khắc phục. Sự kết hợp này mang lại hiệu quả đáng kinh ngạc cho DSU.
3. Độ phức tạp
Phân Tích Trừ Dần
Sau khi áp dụng cả hai tối ưu hóa, độ phức tạp của DSU trở nên phi thường. Để hiểu hiệu suất thực sự, chúng ta cần dùng phân tích trừ dần (amortized analysis), tức là tính chi phí trung bình trên một chuỗi dài các thao tác.
Hãy tưởng tượng một con đường đầy ổ gà. Chuyến đi đầu tiên rất xóc (giống như find trên đường đi sâu). Nhưng nếu trong chuyến đi đó, anh em lấp lại tất cả ổ gà (giống như nén đường đi), thì mọi chuyến đi sau này sẽ cực nhanh. Phân tích trừ dần cho thấy chi phí "dọn dẹp" của một số thao tác tốn kém giúp rất nhiều thao tác trong tương lai rẻ hơn, làm cho chi phí trung bình cực kỳ thấp.
Hàm Ackermann Nghịch Đảo α(n) là gì?
Độ phức tạp thời gian trừ dần của DSU với cả hai tối ưu hóa là , trong đó là hàm Ackermann nghịch đảo.
Thay vì đi sâu vào định nghĩa toán học phức tạp, anh em chỉ cần hiểu một cách trực quan:
- Hàm Ackermann phát triển bùng nổ.
- Hàm Ackermann nghịch đảo, , thì ngược lại: nó phát triển chậm đến mức không thể tưởng tượng được.
Đối với bất kỳ giá trị đầu vào n nào trong thực tế (kể cả số nguyên tử trong vũ trụ), giá trị của sẽ không bao giờ vượt quá 5. Do đó, trong thực tế, có thể được coi là thời gian hằng số trừ dần. Đây là một trong những cấu trúc dữ liệu nhanh nhất mà chúng ta có.
So Sánh Hiệu Suất: Một Chặng Đường
| Triển Khai | Độ Phức Tạp Find (Trừ dần) | Độ Phức Tạp Union (Trừ dần) |
|---|---|---|
| Ngây thơ (Cây suy biến) | ||
| Chỉ có Union by Size/Rank | ||
| Chỉ có Path Compression | ||
| Path Compression + Union by Size/Rank |
Bảng này cho thấy rõ rằng chính sự kết hợp của cả hai tối ưu hóa mới tạo ra hiệu suất phi thường của DSU.
DSU không chỉ là một cấu trúc dữ liệu, nó là một cách tư duy về các vấn đề kết nối. Bằng cách nắm vững nó, anh em đã thêm một trong những công cụ mạnh mẽ và hiệu quả nhất vào bộ công cụ giải quyết vấn đề của mình. Hẹn gặp lại anh em trong phần 2 của DSU!
All rights reserved
