8.9K 674 107

Đã đăng vào thg 12 22, 2023 8:00 SA 19 phút đọc

453

Chia căn (phần 1) - Giới thiệu về Chia căn

I. Giới thiệu

Những bài toán truy vấn đoạn luôn luôn là chủ đề thú vị trong các kì thi lập trình. Một số thao tác truy vấn đoạn đơn giản có thể kể đến là tính tổng đoạn con, tìm max/min đoạn con hay tìm $\text{GCD}$ của đoạn con,...Những thao tác này nếu như không có sự hỗ trợ của các cấu trúc dữ liệu thì sẽ tốn độ phức tạp thời gian là $O(n),$ thường dẫn đến lỗi TLE trong các bài toán multi-testcase.

Chia căn (Squaroot Decomposition) chính là một phương pháp (hay cấu trúc dữ liệu) hiệu quả để hỗ trợ các thao tác trên giảm độ phức tạp xuống còn $O(\sqrt{n}),$ nhanh hơn rất nhiều so với thuật toán duyệt thông thường. Trong bài viết này, tôi sẽ giới thiệu tới các bạn dạng đơn giản nhất của kĩ thuật này: Chia mảng ra làm $\sqrt{n}$ khối (blocks), thường dùng để giải quyết các bài toán truy vấn đoạn.

Ta sẽ cùng phân tích một bài toán kinh điển để hiểu rõ hơn về ý tưởng của phương pháp này:

"Cho một mảng $A$ gồm $n$ phần tử $a_1, a_2, \dots, a_n$ . Hãy xây dựng một cấu trúc dữ liệu để tìm ra tổng của đoạn con $[l, r]$ bất kì chỉ trong $O(\sqrt{n})?$ "

Input:

Dòng đầu tiên chứa số nguyên dương $n$ .
Dòng thứ hai chứa $n$ số nguyên $a_1, a_2, \dots, a_n$ .
Dòng thứ ba chứa số nguyên dương $t$ - số lượng truy vấn.
Trên $t$ dòng tiếp theo, mỗi dòng chứa hai số nguyên dương $l, r \ (1 \le l \le r \le n)$ mô tả một đoạn con cần tính tổng.

Ràng buộc:

$1 \le n \le 10^5$ .
$1 \le a_i \le 10^9; \forall i: 1 \le i \le n$ .
$1 \le t \le 10^4$ .

Output:

Đưa ra trên $t$ dòng, mỗi dòng là tổng của đoạn con tương ứng.

Sample Input:

13
3 1 5 2 1 5 2 1 3 2 6 7 1
3
1 4
3 8
7 13

Sample Output:

11
16
22

II. Phân tích chi tiết

1. Ý tưởng

Tiền xử lý dữ liệu

Ý tưởng cơ bản của Chia căn chính là tiền xử lý. Ta sẽ chia nhỏ mảng $A$ thành các khối (block) có độ dài là $\left\lceil\sqrt{n}\right\rceil$ (có thể tồn tại khối có độ dài nhỏ hơn, tức là không đủ phần tử). Với mỗi khối thứ $i,$ ta gọi $b[i]$ là tổng các phần tử trong khối.

Giả sử cả độ dài các khối lẫn số lượng khối là $s = \left\lceil\sqrt{n}\right\rceil$ . Lúc này, mảng $A$ sẽ được chia thành $s$ khối như sau:

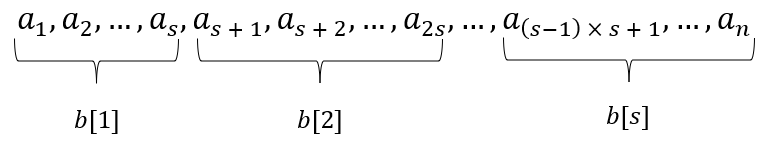
Riêng khối cuối cùng có thể sẽ không có đủ $s$ phần tử, nếu như $n$ không phải là một bội của $s$ . Tuy nhiên điều này không ảnh hưởng tới ý tưởng Chia căn, vì nó có thể được xử lý riêng rất dễ dàng.

Tổng của khối thứ $k$ sẽ được lưu trong phần tử $b[k]$ :

$b[k] = \sum_{i = (k - 1) \times s + 1}^{\text{min}(k \times s, n)} a_i$

Việc tính toán các $b[k]$ có thể thực hiện dễ dàng trong $O(n)$ bằng đoạn code dưới đây:

int s = ceil(sqrt(n * 1.0)); // Số lượng khối và độ dài một khối.

vector < long long > data_preparation(int n, int s, vector < int >& a)
{
    vector < long long > b(s + 1);
    for (int i = 1; i <= n; ++i)
    {
        int id = (i + s - 1) / s; // Chỉ số khối chứa phần tử a[i].
        b[id] += a[i]; 
    }
        
    return b;
}

Xử lý một truy vấn

Giờ giả sử ta đã tính xong các giá trị $b[k],$ liệu nó có thể giúp gì cho việc tính tổng đoạn $[l, r]?$

Nếu như một đoạn $[l, r]$ đủ độ dài, thì nó sẽ bao gồm một hoặc một số khối có đầy đủ phần tử - việc tính tổng các khối này có thể thực hiện chỉ trong một thao tác. Ngoài ra, sẽ có thể có những phần tử dư ra ở hai đầu đoạn $[l, r]$ - chúng sẽ thuộc vào hai khối khác, khi đó ta sẽ tính tổng những phần tử này thủ công.

Ví dụ, với mảng $A = \{3,1,5,2,1,5,2,1,3,2,6,7,1\} \ (n = 13, s = 4)$ thì nó sẽ được chia như sau:

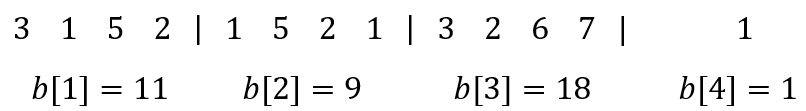
Xét một khối thứ $k$ gồm đầy đủ $s$ phần tử mà nằm trong đoạn $[l, r],$ thì tổng của nó hẳn nhiên đã được lưu trong $b[k]$ . Gọi chỉ số của khối chứa $a_l$ và khối chứa $a_r$ lần lượt là $block_l$ và $block_r,$ ta có công thức:

$\begin{cases}block_l = \left\lceil\frac{l}{s}\right\rceil \\ block_r = \left\lceil\frac{r}{s}\right\rceil\end{cases}$

Các khối độ dài đầy đủ sẽ có chỉ số nằm trong đoạn $[block_l + 1, block_r - 1]$ . Còn các phần tử nằm ở khối chứa $a_l$ và khối chứa $a_r$ - những khối bị thiếu - ta sẽ tính tổng riêng. Chỉ số của phần tử cuối cùng trong khối $block_l$ và phần tử đầu tiên trong khối $block_r$ lần lượt là $end_l = block_l \times s$ và $start_r = (block_r - 1) \times s + 1$

Như vậy, tổng của đoạn $[l, r]$ lúc này sẽ tính bằng công thức:

$\sum_{i = l}^r a_i = \sum_{i = l}^{end_l} a_i + \sum_{i = start_r}^r a_i + \sum_{i = blocl_l + 1}^{block_r - 1} b[i]$

Tuy nhiên, công thức này sẽ sai nếu như một truy vấn có $l$ và $r$ thuộc cùng một khối. Lúc này ta cần phải tính tổng của truy vấn một cách thủ công.

long long query(int l, int r, int n, int s, vector < int >& a, const vector < long long >& b)
{   
    int block_l = (l + s - 1) / s, block_r = (r + s - 1) / s;
    if (block_l == block_r)
        return accumulate(a.begin() + l, a.begin() + r + 1, 0LL);
    
    int end_l = block_l * s, start_r = (block_r - 1) * s + 1;
    long long res = 0;
    res += accumulate(a.begin() + l, a.begin() + end_l + 1, 0LL);
    res += accumulate(a.begin() + start_r, a.begin() + r + 1, 0LL) 
    res += accumulate(b.begin() + block_l + 1, b.begin() + block_r, 0LL);
    
    return res;
}

2. Cài đặt đầy đủ

Trong cài đặt dưới đây, tôi sử dụng định danh #define int long long để đưa kiểu dữ liệu khi tính toán về long long cho phù hợp với ràng buộc của đề bài. Giá trị $s$ cũng được tính sẵn ở hàm main() rồi truyền qua các hàm khác để đỡ phải tính nhiều lần.

#pragma GCC optimize("O3","unroll-loops")
#pragma GCC target("avx2")

#include <bits/stdc++.h>
#define int long long

using namespace std;

vector < int > data_preparation(int n, int s, const vector < int >& a)
{
    vector < int > b(s + 1);
    for (int i = 1; i <= n; ++i)
    {
        int id = (i + s - 1) / s;; // Chỉ số khối chứa phần tử a[i].
        b[id] += a[i];
    }

    return b;
}

int query(int l, int r, int n, int s, const vector < int >& a, const vector < int >& b)
{    
    int block_l = (l + s - 1) / s, block_r = (r + s - 1) / s;
    if (block_l == block_r)
        return accumulate(a.begin() + l, a.begin() + r + 1, 0LL);

    int end_l = block_l * s, start_r = (block_r - 1) * s + 1;
    int res = 0;
    res += accumulate(a.begin() + l, a.begin() + end_l + 1, 0LL);
    res += accumulate(a.begin() + start_r, a.begin() + r + 1, 0LL);
    res += accumulate(b.begin() + block_l + 1, b.begin() + block_r, 0LL);

    return res;
}

signed main()
{
    ios_base::sync_with_stdio(false);
    cin.tie(nullptr);
    
    int n;
    cin >> n;

    vector < int > a(n + 1);
    for (int i = 1; i <= n; ++i)
        cin >> a[i];
    
    int s = ceil(sqrt(n * 1.0)); // Số lượng khối và độ dài một khối.
    vector < int > b = data_preparation(n, s, a);

    int t;
    cin >> t;

    while (t--)
    {
        int l, r;
        cin >> l >> r;

        cout << query(l, r, n, s, a, b) << '\n';
    }

    return 0;
}

4. Đánh giá

Độ phức tạp thời gian

Giả sử số đoạn chia ra là $s,$ vậy mỗi đoạn có độ dài là $\left\lfloor{\frac{n}{s}}\right\rfloor$ .

Đối với mỗi truy vấn, ta phải xét các đoạn đầy đủ và các đoạn thiếu ở hai đầu:

Đối với các đoạn đầy đủ, trường hợp tệ nhất ta phải xét đủ cả $s$ đoạn, mỗi đoạn ta đã tính trước $b[k],$ do đó tổng độ phức tạp là $O(s)$ .
Đối với các đoạn thiếu, xét riêng mỗi phần tử mất $O(1)$ . Mỗi đoạn có độ dài tối đa $\left\lfloor{\frac{n}{s}}\right\rfloor,$ do đó tối đa ta mất $O\left(\left\lfloor{\frac{n}{s}}\right\rfloor\right)$ cho bước này.

Như vậy, mỗi truy vấn ta mất tổng đpt $O\left(s + \left\lfloor{\frac{n}{s}}\right\rfloor\right)$ . Áp dụng bất đẳng thức Cauchy với hai số không âm $s$ và $\left\lfloor{\frac{n}{s}}\right\rfloor,$ ta thấy $s + \left\lfloor{\frac{n}{s}}\right\rfloor$ đạt giá trị nhỏ nhất bằng $\sqrt{n},$ khi và chỉ khi $s = \left\lfloor{\frac{n}{s}}\right\rfloor,$ tức là $s = \left\lceil\sqrt{n}\right\rceil$ và độ phức tạp sẽ tiến tới $O\left(2\sqrt{n}\right)$ cho mỗi truy vấn.

Độ phức tạp không gian

Các mảng sử dụng chỉ tốn tối đa $O(n)$ cho không gian lưu trữ. Vì thế, độ phức tạp không gian tổng quát cũng là $O(n)$ .

III. Mở rộng cho thao tác cập nhật

1. Cập nhật một phần tử

Điều thú vị của kĩ thuật Chia căn nằm ở việc nó có thể hỗ trợ cả thao tác cập nhật một phần tử trong mảng, hoặc cập nhật lại đoạn trên mảng. Nếu như ở kĩ thuật Mảng tổng tiền tố, ta phải thay đổi lại cả mảng tổng khi có thao tác cập nhật, thì trong kĩ thuật Chia căn ta chỉ cần cập nhật lại khối chứa phần tử bị thay đổi.

Giả sử ta cần cập nhật lại $a_p = x,$ thì ta chỉ cần cập nhật lại khối chứa $a_p$ là $k = \left\lceil\frac{i}{s}\right\rceil,$ sau đó cập nhật lại $a_p = x$ .

$\begin{cases}b[k] = b[k] - a_p + x \\ a_p = x \end{cases}$

Thao tác này chỉ mất $O(1)$ . Thậm chí, bài toán có thể thay đổi thành tìm giá trị lớn nhất/giá trị nhỏ nhất trong các đoạn $[l, r]$ (bài toán RMQ) - ta chỉ cần xây dựng lại mảng $b[k]$ theo cách hoàn toàn tương tự như tính tổng, tuy nhiên đối với thao tác cập nhật phần tử thì cần lưu ý cập nhật lại tất cả khối chứa $a_i$ bị thay đổi - mất độ phức tạp chỉ là $O(\sqrt{n})$ :

void update(int x, int p, int n, int s, const vector < int >& a, vector < int >& b)
{   
    int block = (p + s - 1) / s;
    int min_id = (block - 1) * s + 1, max_id = block * s;
    
    a[p] = x;
    b[block] = a[min_id];
    for (int i = min_id + 1; i <= max_id; ++i)
        b[block] = max(b[block], a[i]); // Hoặc b[block] = min(b[block], a[i]).
}

2. Cập nhật đoạn

Chia căn cũng có thể sử dụng cho thao tác cập nhật một đoạn phần tử tăng/giảm giá trị hoặc thay đổi thành giá trị khác.

Giả định ta có hai loại truy vấn trong bài toán, một là tăng đoạn $[l, r]$ lên $x$ đơn vị, hai là in ra giá trị của phần tử $a_p$ . Lúc này, ta vận dụng Chia căn như sau:

Sử dụng mảng $b[k]$ để lưu trữ tổng giá trị cần phải tăng thêm cho toàn bộ phần tử thuộc khối $k$ (ban đầu tất cả các $b[k] = 0$ ). Có nghĩa là ta sẽ lưu trữ riêng các giá trị cập nhật của các đoạn đầy đủ ra một mảng.
Với thao tác tăng đoạn $[l, r],$ ta cần lặp qua tất cả các khối $k$ có đủ độ dài $s = \left\lceil\sqrt{n}\right\rceil$ và gán $b[k] = b[k] + x$ - với ý nghĩa là các phần tử thuộc khối $k$ đã được tăng thêm $x$ đơn vị. Còn các phần tử $a_i$ ở hai đầu đoạn mà không thuộc vào các khối đầy đủ thì ta sẽ tăng trực tiếp các $a_i$ đó lên. Thao tác này có độ phức tạp $O(\sqrt{n})$ .
Với thao tác in ra giá trị của $a_p,$ ta chỉ cần tìm ra chỉ số khối chứa $a_p$ là $block = \left\lceil\frac{p}{s}\right\rceil$ rồi đưa ra kết quả là $a_p + b[block]$ . Thao tác này chỉ có độ phức tạp $O(1)$ .

// Hàm update trực tiếp lên mảng A.
void manual_update(int l, int r, int x, vector < int >& a)
{
    for (int i = l; i <= r; ++i)
        a[i] += x;
}

// Update cho một truy vấn [l, r].
void update(int l, int r, int x, int n, int s, vector < int >& a, vector < int >& b)
{
    int block_l = (l + s - 1) / s, block_r = (r + s - 1) / s;
    if (block_l == block_r)
    {
        manual_update(l, r, x, a);
        return;
    }

    int end_l = block_l * s, start_r = (block_r - 1) * s + 1;
    manual_update(l, end_l, x, a);
    manual_update(start_r, r, x, a);
    for (int i = block_l + 1; i < block_r; ++i)
        b[i] += x;
}

// Trả về giá trị của phần tử a[p].
int get_value(int p, int n, int s, vector < int >& a, vector < int >& b)
{
    int block = (p + s - 1) / s;

    return a[p] + b[block];
}

IV. Một số lưu ý bổ sung

Có rất nhiều cấu trúc dữ liệu khác hỗ trợ thao tác tính toán và cập nhật trên đoạn một cách hiệu quả, chẳng hạn như Segment Tree, tuy nhiên Chia căn vẫn luôn luôn được yêu thích bởi cài đặt đơn giản, dễ nhớ, và đặc biệt nó có thể áp dụng cho nhiều dạng bài khác nhau dựa trên ý tưởng chia dãy số thành $\sqrt{n}$ đoạn để xử lý riêng biệt.

Những bài toán thao tác trên đoạn mà giới hạn input nhỏ như $n \le 5 \times 10^4$ hoặc ràng buộc thời gian lớn như $\ge 2s$ có thể là dấu hiệu cho việc áp dụng Chia căn.

Trên thực tế, ta không nhất thiết phải đặt chính xác $s = \left\lceil\sqrt{n}\right\rceil,$ mà sẽ tùy thuộc vào bài toán và kích thước input để chọn ra một kích thước đoạn tối ưu. Chẳng hạn, một số trường hợp như sau có thể lưu ý:

Nếu bài toán chỉ đi qua các khối mà hầu như không thao tác với từng phần tử trong mỗi khối, thì sẽ tốt hơn khi đặt $s < \left\lceil\sqrt{n}\right\rceil$ để làm giảm số khối đi, khi đó số phần tử trong mỗi khối sẽ $> \left\lceil\sqrt{n}\right\rceil$ .
Nếu như một thao tác update có độ phức tạp tỉ lệ thuận với kích thước khối - tức là $\approx O(c \times s)$ và một thao tác truy vấn kết quả có độ phức tạp tỉ lệ thuận với số lượng khối nhân với $\log n$ - tức là $\approx O(c \times s \times \log n);$ thì ta có thể đặt $s \approx \sqrt{\frac{n}{\log n}}$ để làm cho cả hai thao tác có độ phức tạp giảm xuống còn $O(n \times \log n)$ .

V. Bài tập minh họa

1. Đếm giá trị

Đề bài

Cho dãy gồm $n$ số nguyên dương $a_1,a_2,…,a_n$ . Với mỗi dãy con $a_l,a_{l + 1},…,a_r \ (1≤l≤r≤n)$ và số nguyên dương $k;$ đặt $F_k$ là số lần xuất hiện của $k$ trong dãy con đó.

Ví dụ, cho dãy gồm $8$ số nguyên $\{1,1,2,2,1,3,1,1\}$ . Dãy con với $(l=2, r=7)$ có $F_1=3,F_2=2,F_3=1;$ còn với $k > 3$ thì $F_k=0$ .

Yêu cầu: Cho $T$ dãy con dạng $(l, r, k);$ hãy xác định giá trị $F_k$ của mỗi dãy con?

Input:

Dòng đầu tiên chứa hai số nguyên dương $n$ và $T$ .
Dòng thứ hai chứa $n$ số nguyên dương $a_1, a_2, \dots, a_n$ phân tách nhau bởi dấu cách.
Trên $T$ dòng tiếp theo, mỗi dòng chứa ba số nguyên dương $l, r, k$ thể hiện một dãy con.

Ràng buộc:

$1 \le n, T \le 2 \times 10^5$ .
$1 \le a_i \le 10^9; \forall i: 1 \le i \le n$ .

Output:

Gồm $T$ dòng, dòng thứ $i$ ghi một số nguyên là kết quả của câu hỏi thứ $i$ .

Sample Input:

6 3
1 1 5 3 3 6
1 3 1
1 5 3
2 5 3

Sample Output:

2
2
2

Ý tưởng

Để đếm số lần xuất hiện của các giá trị trong mảng, phương pháp đơn giản nhất ta có thể nghĩ tới là Đếm phân phối. Giả sử bài toán luôn luôn có $l = 1$ và $r = n$ thì ta dễ dàng giải quyết nó bằng cách gọi $cnt[x]$ là số lần xuất hiện của giá trị $x$ trong mảng.

Áp dụng ý tưởng trên, ta sẽ tạo ra $\sqrt{n}$ mảng $cnt$ để kiểm soát số lần xuất hiện của các phần tử trong $\sqrt{n}$ đoạn của mảng $A$ . Đặt $cnt[i][x]$ là số lần xuất hiện của giá trị $x$ trong khối thứ $i,$ ta dễ dàng tính ra toàn bộ các mảng $cnt$ chỉ trong $O(n)$ .

Lúc này với mỗi truy vấn $(l, r, k)$ ta sẽ tính tổng tất cả các $cnt[i][k]$ thỏa mãn $i$ là các khối đầy đủ thuộc đoạn $[l, r]$ . Còn các phần tử bị dư ra ở hai đầu đoạn $[l, r]$ thì ta sẽ xét từng phần tử bằng vòng lặp để đếm số lượng giá trị bằng với $k$ .

Tuy nhiên, do các giá trị $a_i \le 10^9,$ nên để thực hiện được đếm phân phối, trước hết mảng $A$ cần được rời rạc hóa. Khi đó với mỗi truy vấn $(l, r, k),$ ta sẽ đưa về bài toán đếm số lượng giá trị $k'$ trong đoạn $[l, r]$ - với $k'$ là giá trị của $k$ sau khi rời rạc hóa.

Độ phức tạp: $O(n + T \times 2\sqrt{n})$ .

Cài đặt

#pragma GCC optimize("O3","unroll-loops")
#pragma GCC target("avx2")

#include <bits/stdc++.h>
#define int long long

using namespace std;

vector < int > digitize(int n, vector < int >& a)
{
    map < int, vector < int > > id_list;
    for (int i = 1; i <= n; ++i)
        id_list[a[i]].push_back(i);

    int counter = 0;
    vector < int > digi_val(n + 1);
    for (auto e: id_list)
    {
        ++counter;

        for (int p: e.second)
            a[p] = counter;

        digi_val[e.first] = counter;
    }

    return digi_val;
}

vector < vector < int > > data_preparation(int n, int s, const vector < int >& a)
{
    vector < vector < int > > cnt(s + 1, vector < int >(n + 1));
    for (int i = 1; i <= n; ++i)
    {
        int id = (i + s - 1) / s;; // Chỉ số khối chứa phần tử a[i].
        ++cnt[id][a[i]];
    }

    return cnt;
}

int query(int l, int r, int k, int n, int s, vector < int >& a, vector < vector < int > >& cnt)
{
    int block_l = (l + s - 1) / s, block_r = (r + s - 1) / s;
    if (block_l == block_r)
        return count(a.begin() + l, a.begin() + r + 1, k);

    int end_l = block_l * s, start_r = (block_r - 1) * s + 1;
    int res = 0;
    res += count(a.begin() + l, a.begin() + end_l + 1, k);
    res += count(a.begin() + start_r, a.begin() + r + 1, k);
    for (int i = block_l + 1; i < block_r; ++i)
        res += cnt[i][k];

    return res;
}

signed main()
{
    ios_base::sync_with_stdio(false);
    cin.tie(nullptr);
    
    int n, t;
    cin >> n >> t;

    vector < int > a(n + 1);
    for (int i = 1; i <= n; ++i)
        cin >> a[i];

    int s = ceil(sqrt(n * 1.0));
    vector < int > digi_val = digitize(n, a);
    vector < vector < int > > cnt = data_preparation(n, s, a);

    while (t--)
    {
        int l, r, k;
        cin >> l >> r >> k;

        if (!digi_val[k])
            cout << 0 << '\n';
        else
            cout << query(l, r, digi_val[k], n, s, a, cnt) << '\n';
    }

    return 0;
}

2. Holes

Tý đang chơi một trò chơi có tên là "Holes". Trò chơi này có quy tắc như sau:

Có $n$ cái hố nằm trên đường thẳng được đánh số từ $1$ tới $n,$ hố thứ $i$ có sức mạnh $p_i$ . Nếu như Tý ném một quả bóng vào hố thứ $i$ thì ngay lập tức nó sẽ nhảy sang hố thứ $i + p_i,$ rồi cứ tiếp tục như vậy cho tới khi không còn hố nào để nhảy được nữa thì quả bóng sẽ nhảy ra khỏi hàng.

Tý được phép thực hiện $m$ lượt chơi, ở mỗi lượt cậu sẽ làm một trong hai thao tác:

Thao tác $1$ : Đặt sức mạnh của hố $a$ thành $b$ .
Thao tác $2$ : Ném một quả bóng vào hố $a,$ rồi đếm số bước nhảy của nó cho tới khi nó nhảy ra khỏi hàng, đồng thời ghi lại chỉ số của hố cuối cùng mà quả bóng nhảy vào trước khi nó ra khỏi hàng.

Yêu cầu: Cho danh sách $m$ lượt chơi mà Tý thực hiện, hãy đưa ra đáp án của các lượt chơi mà Tý làm thao tác số $2?$

Input:

Dòng đầu tiên chứa hai số nguyên dương $n$ và $m$ .
Dòng thứ hai chứa $n$ số nguyên dương $a_1, a_2, \dots, a_n$ phân tách nhau bởi dấu cách.
Trên $m$ $m$ dòng tiếp theo, mỗi dòng chứa thông tin về một lượt chơi của Tý:
- Đầu tiên là số nguyên $type$ thể hiện loại thao tác của lượt chơi này. Giá trị của $type = 0$ tương ứng với thao tác loại $1$ và $type = 1$ tương ứng với thao tác loại $2$ .
- Nếu $type = 0$ thì theo sau là hai số nguyên dương $a, b;$ ngược lại thì theo sau là một số nguyên dương $a$ .

Ràng buộc:

$1 \le n, m \le 10^5$ .
$1 \le p_i \le n; \forall i: 1 \le i \le n$ .
$1 \le a, b \le n$ .

Output:

Với mỗi thao tác loại $2,$ đưa ra hai số nguyên lần lượt là chỉ số của hố cuối cùng mà quả bóng nhảy vào, và số bước nhảy cho tới khi quả bóng rời khỏi hàng (tính cả bước nhảy ra khỏi hàng).

Sample Input:

8 5
1 1 1 1 1 2 8 2
1 1
0 1 3
1 1
0 3 4
1 2

Sample Output:

8 7
8 5
7 3

Ý tưởng

Ta sẽ chia các hố thành $s = \left\lceil\sqrt{n}\right\rceil$ khối liên tiếp.

Với mỗi hố $i$ , ta sẽ lưu trữ thêm hai giá trị sau:

$nxt[i]$ : Chỉ số của hố đầu tiên nằm khác khối với hố $i,$ mà từ hố $i$ có thể nhảy tới được. Nếu từ $i$ không thể nhảy được tới hố nào trong dãy thì coi $nxt[i] = i$ .
$cnt[i]$ : Số bước nhảy để từ hố $i$ tới được hố $nxt[i]$ . Nếu $nxt[i] = i$ thì $cnt[i] = 0$ .

Hai mảng này sẽ được xây dựng bằng Quy hoạch động như sau:

Ban đầu ta tính toán từng $nxt[i]$ và $cnt[i]$ chỉ với một bước nhảy sang hố tiếp theo, coi như đây là cơ sở quy hoạch động.
Xét các hố $i$ từ $n$ về $1,$ ta biết rằng hố tiếp theo nó sẽ nhảy tới là $i + p_i$ . Nếu như $i + p_i > n$ hoặc $i + p_i$ đã nằm ở khối khác với khối chứa $i$ thì giữ nguyên $nxt[i]$ và $cnt[i]$ . Ngược lại thì ta sẽ "nhảy cóc" sang hố phía sau hố $i + p_i$ :
$nxt[i] = nxt[i + p_i], cnt[i] = 1 + cnt[i + p_i]$

Bây giờ ta xét các loại truy vấn:

Loại $1$ : Đặt $p_a = b$ . Khi đó ta phải cập nhật lại các giá trị $nxt[a], cnt[a]$ và cả các giá trị $nxt[i], cnt[i]$ của các hố $i$ nằm cùng một khối với hố $a \ (i < a)$ . Lưu ý bước này ta phải cập nhật lại từ các hố ở phía sau lùi dần ra phía trước (giống ở bước khởi tạo). Do độ dài một khối là $s = \left\lceil\sqrt{n}\right\rceil$ nên thao tác này sẽ diễn ra trong $O(\sqrt{n})$ .
Loại $2$ : Nhảy từ hố $a$ tới khi ra khỏi hàng. Bước này ta chỉ cần liên tục nhảy từ $a$ sang $nxt[a]$ cho tới khi $nxt[a] = a,$ đồng thời cộng $cnt[a]$ vào kết quả. Do ta nhảy cóc từ khối này sang khối khác, nên bước này cũng chỉ tốn tối đa $O(\sqrt{n})$ .

Như vậy, thông qua kĩ thuật chia căn, ta có thuật toán với độ phức tạp $O\left(n + m \times \sqrt{n}\right)$ .

Cài đặt

Bên dưới là cài đặt mẫu của bài toán, các bạn có thể nộp thử ở link sau: CF Beta 13 - Holes.

Tuy nhiên, bài toán này có ràng buộc thời gian và bộ nhớ khá chặt, nên các mảng đều được cài đặt mảng tĩnh để tăng tốc độ chương trình. Ngoài ra, việc kiểm tra hai phần tử $x$ và $y$ có cùng một khối hay không cũng được đơn giản hóa thông qua phép kiểm tra x / s == y / s - để giảm bớt độ phức tạp của các phép cộng trừ.

#pragma GCC optimize("O3","unroll-loops")
#pragma GCC target("avx2")

#include <bits/stdc++.h>

using namespace std;

const int maxn = 1e5 + 1;
int n, m, s;
int p[maxn], nxt[maxn], cnt[maxn];

// Kiểm tra xem hai hố x và y có nằm ở hai khối khác nhau không.
bool check_diff_block(const int& x, const int& y)
{
    int block_x = x / s, block_y = y / s;
    return block_x != block_y;
}

void data_preparation()
{
    for (int i = 1; i <= n; ++i)
        if (i + p[i] <= n) // Nếu từ i nhảy tới hố tiếp theo trong hàng thì đặt nxt[i] = i + p[i].
        {
            nxt[i] = i + p[i];
            cnt[i] = 1; // Trước tiên chỉ lưu một bước nhảy tới hố tiếp theo.
        }
        else
            nxt[i] = i; // Nếu từ i sẽ nhảy ra khỏi hàng thì đặt nxt[i] = i.

    // Quy hoạch động.
    for (int i = n; i >= 1; --i)
        if (i + p[i] > n || check_diff_block(i, i + p[i]))
            continue;
        else
        {
            nxt[i] = nxt[i + p[i]];
            cnt[i] = 1 + cnt[i + p[i]];
        }
}

void update(const int& a, const int& b)
{
    // Cập nhật lại sức mạnh của hố a thành b.
    p[a] = b;

    // Khi thay đổi sức mạnh của hố a thành b, cần phải update lại các giá trị nxt[i] và cnt[i]
    // của chính hố a và cả các hố i đứng trước hố a mà thuộc cùng một khối với hố a.
    int same_a = a;
    while (same_a >= 1 && !check_diff_block(same_a, a))
    {
        if (same_a + p[same_a] > n)
        {
            nxt[same_a] = same_a;
            cnt[same_a] = 0;
            --same_a;

            continue;
        }

        if (check_diff_block(same_a, same_a + p[same_a]))
        {
            nxt[same_a] = same_a + p[same_a];
            cnt[same_a] = 1;
        }
        else
        {
            nxt[same_a] = nxt[same_a + p[same_a]];
            cnt[same_a] = 1 + cnt[same_a + p[same_a]];
        }

        --same_a;
    }
}

void query(const int& a)
{
    int steps = 0, pos = a;
    while (pos != nxt[pos])
    {
        steps += cnt[pos];
        pos = nxt[pos];
    }

    cout << pos << ' ' << steps + 1 << '\n';
}

signed main()
{
    ios_base::sync_with_stdio(false);
    cin.tie(nullptr);

    cin >> n >> m;

    for (int i = 1; i <= n; ++i)
        cin >> p[i];

    s = ceil(sqrt(n));
    data_preparation();

    while (m--)
    {
        int type;
        cin >> type;

        if (!type)
        {
            int a, b;
            cin >> a >> b;

            update(a, b);
        }
        else
        {
            int a;
            cin >> a;

            query(a);
        }
    }

    return 0;
}

Danh sách bài tập luyện tập

Để tiếp tục theo dõi phần 2 của series bài viết về Chia căn, mời các bạn nhấn vào đây.

VI. Tài liệu tham khảo

I. Giới thiệu

II. Phân tích chi tiết

1. Ý tưởng

Tiền xử lý dữ liệu

Xử lý một truy vấn

2. Cài đặt đầy đủ

4. Đánh giá

Độ phức tạp thời gian

Độ phức tạp không gian

III. Mở rộng cho thao tác cập nhật

1. Cập nhật một phần tử

2. Cập nhật đoạn

IV. Một số lưu ý bổ sung

V. Bài tập minh họa

1. Đếm giá trị

Đề bài

Ý tưởng

Cài đặt

2. Holes

Ý tưởng

Cài đặt

Danh sách bài tập luyện tập

VI. Tài liệu tham khảo

Mục lục