13.0K 210 45

Đã đăng vào khoảng 9 giờ trước 15 phút đọc

Cây chỉ số nhị phân (Binary Indexed Tree/Fenwick Tree) - Phần 1

Xin chào anh em, lại là tôi Jim đây!

Hôm nay, chúng ta sẽ cùng nhau chinh phục một trong những cấu trúc dữ liệu đơn giản mà mạnh mẽ trong lập trình thi đấu: Cây Chỉ Số Nhị Phân, hay còn gọi là Fenwick Tree (BIT).

Hành trình của chúng ta sẽ đi từ bài toán cơ bản nhất, vấp phải những giới hạn của các cách giải quyết thông thường, và rồi BÙM… khai sáng với vẻ đẹp của BIT. Bắt đầu thôi!

1. Bài Toán Truy Vấn Tổng Trên Đoạn

Trong thế giới thuật toán, mọi thứ thường bắt đầu từ một bài toán trông có vẻ đơn giản: Truy vấn Tổng trên Đoạn (Range Sum Query - RSQ).

Bài toán: Cho mảng A có N phần tử và Q truy vấn. Mỗi truy vấn gồm 2 số nguyên L và R, nhiệm vụ của bạn là tính tổng các phần tử của mảng A có chỉ số nằm trong đoạn [L, R].

Cách tiếp cận "ngây thơ"

Ý tưởng đầu tiên và tự nhiên nhất là dùng một vòng lặp for chạy từ L đến R rồi cộng dồn chúng lại.

Độ phức tạp: Mỗi truy vấn tốn $O(N)$ ở trường hợp xấu nhất. Với hàng triệu truy vấn, cách này chắc chắn sẽ "ăn" TLE (Time Limit Exceeded).

Cải tiến với Mảng Cộng Dồn (Prefix Sum)

Để tối ưu, chúng ta có thể dùng Mảng Cộng Dồn. Ta tạo một mảng prefixSum trong đó prefixSum[i] lưu tổng của các phần tử từ có chỉ số nằm trong đoạn [1, i].

Ý tưởng: Tổng của đoạn [L, R] sẽ được tính bằng một phép trừ siêu nhanh: prefixSum[R] - prefixSum[L - 1].
Độ phức tạp:
- Tiền xử lý: $O(N)$ để xây dựng mảng.
- Truy vấn: Chỉ $O(1)$ cho mỗi lần hỏi. Quá tuyệt!

Đây là giải pháp tối ưu cho các bài toán có dữ liệu tĩnh (không thay đổi).

Vậy khi dữ liệu thay đổi thì sao?

Mảng Cộng Dồn rất mạnh, nhưng nó có một điểm yếu chí mạng. Điều gì xảy ra nếu chúng ta có thêm 1 truy vấn nữa có dạng i val và cần phải cập nhật A[i] = val?

Khi một giá trị A[i] thay đổi, toàn bộ mảng prefixSum từ vị trí i trở đi đều sai. Để sửa, chúng ta phải tính lại cả đoạn sau, việc này tốn $O(N)$ .

Lúc này, chúng ta rơi vào tình thế tiến thoái lưỡng nan:

Dùng mảng gốc: Cập nhật $O(1)$ , truy vấn $O(N)$ .
Dùng mảng cộng dồn: Cập nhật $O(N)$ , truy vấn $O(1)$ .

Nếu bài toán yêu cầu cả hai thao tác này xen kẽ với số lượng lớn, cả hai cách trên đều không ổn. Chúng ta cần một cấu trúc dữ liệu có thể cân bằng cả hai. Và đó là lúc người hùng của chúng ta xuất hiện.

2. Cây Chỉ Số Nhị Phân (Binary Indexed Tree - Fenwick Tree)

Cây Chỉ Số Nhị Phân (Binary Indexed Tree - BIT), do Peter Fenwick đề xuất năm 1994, ra đời để giải quyết chính xác bài toán trên. Nó đạt được sự cân bằng đáng kinh ngạc: cả cập nhật điểm và truy vấn tổng tiền tố đều chỉ mất $O(\log N)$ .

Dù tên là "cây", BIT thường được cài đặt bằng một mảng thông thường. Sức mạnh của nó nằm ở cấu trúc ngầm định, nơi mối quan hệ cha-con được suy ra từ chỉ số thông qua các phép toán bit.

Least Significant Bit (LSB)

LSB(i) là bit 1 nhỏ nhất (bit 1 đầu tiên xét từ phải qua trái) trong biểu diễn nhị phân của i.
Về giá trị, nó tương ứng với lũy thừa của 2 tại vị trí đó. Hay nói các khác thì giá trị của LSB(i) chính là lũy thừa của 2 lớn nhất mà có thể được chia hết bởi i.
- Ví dụ:
  - i = 6 (nhị phân 110): Bit 1 đầu tiên tính từ phải qua trái là ví trí 1. Vậy LSB(i) = $2^1 = 2$ .
  - i = 12 (nhị phân 1100): Bit 1 đầu tiên tính từ phải qua trái là ví trí 2. Vậy LSB(i) = $2^2 = 4$ .

Giải mã cơ chế hoạt động

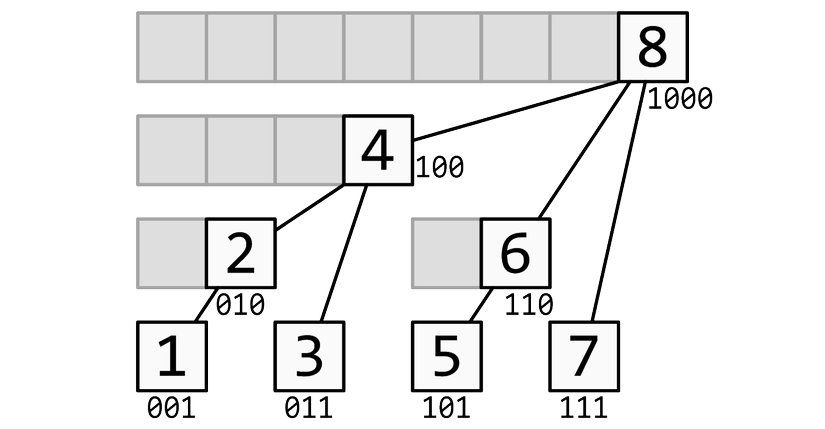
Điều cốt lõi nhất cần nhớ: BIT[i] không lưu tổng từ 1 đến i. Thay vào đó, mỗi phần tử BIT[i] chịu trách nhiệm cho một "vùng" cụ thể.

Vùng trách nhiệm của BIT[i] là tổng của một đoạn con trong mảng gốc, kết thúc tại i và có độ dài bằng giá trị của bit 1 có trọng số nhỏ nhất (Least Significant Bit - LSB) trong biểu diễn nhị phân của i.

Công thức đoạn:

${BIT}[i] = \sum_{k = i - \text{LSB}(i) + 1}^{i} A_k$

Chỉ số k chạy từ phần tử đầu vùng trách nhiệm đến i.
$\text{LSB}(i)$ cho biết độ dài đoạn mà BIT[i] “ôm trọn”.

Ví dụ:

Với i = 12: $\text{LSB}(12) = 4 \Rightarrow \text{BIT}[12] = \sum_{k = 9}^{12} A_k = A_9 + A_{10} + A_{11} + A_{12}$
Với i = 6: $\text{LSB}(6) = 2 \Rightarrow \text{BIT}[6] = \sum_{k = 5}^{6} A_k = A_5 + A_6$

Phép toán bit: `i & -i`

Làm sao để tìm giá trị của LSB một cách nhanh chóng? Câu trả lời nằm ở thủ thuật bitwise: i & -i. Phép toán này sẽ trả về một số mà chỉ có bit ở vị trí LSB của i được giữ lại.

Điều này hoạt động dựa trên cách máy tính biểu diễn số âm bằng phương pháp bù 2. Khi thực hiện phép AND giữa i và -i, chỉ có bit LSB chung được giữ lại.

Cách tính -i theo phương pháp bù 2: Ta có -i = ~i + 1. Tức là ta đảo các bit của i (Từ 0 thành 1 và ngược lại) sau đó cộng thêm 1.

i (Thập phân)	i (Nhị phân)	-i (Bù 2)	i & -i (Nhị phân)	i & -i (Thập phân)	Vùng Trách Nhiệm của BIT[i] (tổng các phần tử A)
1	0001	1111	0001	1	$\sum_{k = 1}^{1} A_k$
2	0010	1110	0010	2	$\sum_{k = 1}^{2} A_k$
3	0011	1101	0001	1	$\sum_{k = 3}^{3} A_k$
4	0100	1100	0100	4	$\sum_{k = 1}^{4} A_k$
5	0101	1011	0001	1	$\sum_{k = 5}^{5} A_k$
6	0110	1010	0010	2	$\sum_{k = 5}^{6} A_k$
7	0111	1001	0001	1	$\sum_{k = 7}^{7} A_k$
8	1000	1000	1000	8	$\sum_{k = 1}^{8} A_k$
12	1100	0100	0100	4	$\sum_{k = 9}^{12} A_k$

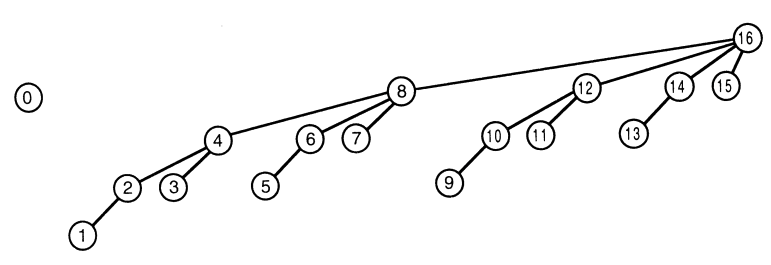
Anh em cũng có thể hình dung cây BIT của chúng ta theo hình phía dưới: Node i sẽ có "vùng trách nhiệm" là cây con gốc i trên cây.

Hàm `update` và `query`

Sự kỳ diệu của BIT nằm ở tính đối xứng của hai thao tác chính:

query(idx) - Tính tổng tiền tố từ 1 đến idx:
- Bắt đầu từ BIT[idx], cộng vào kết quả.
- "Nhảy" về phía sau (Nhảy về node lớn nhất không phải là con của nó) bằng phép idx -= (idx & -idx).
- Lặp lại cho đến khi idx bằng 0.
- Về bản chất, chúng ta đang chia đoạn [1, idx] thành các khối có độ dài là lũy thừa của 2.
- Ví dụ query(13) (nhị phân 1101): sum = BIT[13] + BIT[12] + BIT[8].
update(idx, delta) - Cập nhật giá trị tại idx:
- Khi A[idx] thay đổi một lượng delta, ta cần cập nhật tất cả các BIT[j] mà vùng trách nhiệm của nó chứa idx.
- Bắt đầu từ BIT[idx], cộng delta vào nó.
- "Nhảy" lên "cha" bằng phép idx += (idx & -idx).
- Lặp lại cho đến khi idx vượt ra ngoài kích thước mảng.
- Ví dụ update(5, delta) (nhị phân 101): Cập nhật BIT[5], BIT[6], BIT[8], BIT[16], ...

Cài đặt trong C++

Để đơn giản hóa, chúng ta thường dùng chỉ số 1-based (Chỉ số của mảng bắt đầu từ 1) cho mảng BIT. Đây là một cài đặt hoàn chỉnh:

#include <bits/stdc++.h>

using namespace std;

class FenwickTree
{
private:
	vector<long long> bit; // Mảng BIT, 1-based indexing
	int size;

public:
	// Constructor: Khởi tạo cây với kích thước n
	FenwickTree(int n)
	{
		size = n;
		bit.assign(n + 1, 0);
	}

	// Cập nhật: Cộng thêm delta vào phần tử tại chỉ số idx
	// Độ phức tạp: O(log N)
	void update(int idx, int delta)
	{
		while (idx <= size)
		{
			bit[idx] += delta;
			idx += idx & -idx; // Di chuyển lên cha
		}
	}

	// Truy vấn: Tính tổng tiền tố từ 1 đến idx
	// Độ phức tạp: O(log N)
	long long query(int idx)
	{
		long long sum = 0;
		while (idx > 0)
		{
			sum += bit[idx];
			idx -= idx & -idx; // Di chuyển đến node lớn nhất không phải là con của idx
		}
		return sum;
	}

	// Truy vấn tổng trên đoạn [L, R]
	// Độ phức tạp: O(log N)
	long long queryRange(int L, int R)
	{
		if (L > R)
			return 0;
		return query(R) - query(L - 1);
	}
};

int main()
{
	ios::sync_with_stdio(0);
	cin.tie(0);

	vector<int> a = {3, 2, -1, 6, 5, 4, -3, 3, 7, 2, 3};
	int n = a.size();
	FenwickTree ft(n);

	// Xây dựng cây BIT từ mảng ban đầu
	for (int i = 0; i < n; ++i)
		ft.update(i + 1, a[i]); // Chuyển sang 1-based index

	// Truy vấn tổng đoạn [3, 7] (1-based)
	// Tương ứng chỉ số 2 đến 6 trong mảng gốc: -1 + 6 + 5 + 4 + -3 = 11
	cout << "Sum of range [3, 7]: " << ft.queryRange(3, 7) << endl;

	// Cập nhật phần tử thứ 5 (giá trị 5) thành 10 (cộng thêm 5)
	ft.update(5, 5);

	// Truy vấn lại
	// -1 + 6 + 10 + 4 + -3 = 16
	cout << "Sum after update: " << ft.queryRange(3, 7) << endl;
	return 0;
}

Với cấu trúc dữ liệu này, chúng ta đã phá vỡ được bức tường thử thách, đạt hiệu suất $O(\log N)$ cho cả hai thao tác.

Kỳ Phùng Địch Thủ: BIT vs. Cây Phân Đoạn (Segment Tree)

Đây là câu hỏi kinh điển: "Khi nào dùng BIT, khi nào dùng Segment Tree?".

BIT là một cỗ máy dựa trên tổng tiền tố. Nó hoạt động tốt với các phép toán có tính nghịch đảo (cộng/trừ, XOR).
Segment Tree là một cỗ máy chia để trị. Nó có thể hoạt động với bất kỳ phép toán có tính kết hợp nào (min, max, GCD...).

Tiêu chí	Cây Chỉ Số Nhị Phân (BIT)	Cây Phân Đoạn (Segment Tree)
Độ phức tạp	$O(\log N)$	$O(\log N)$
Không gian lưu trữ	$O(N)$	$O(4N)$
Loại truy vấn	Tổng tiền tố, các phép toán có nghịch đảo.	Đoạn bất kỳ (min, max, sum...), phép toán kết hợp.
Cập nhật đoạn	Phức tạp, cần kỹ thuật bổ sung.	Hỗ trợ tốt với Lazy Propagation.
Độ khó cài đặt	Dễ, code ngắn gọn, ít lỗi vặt.	Trung bình, code dài hơn, cần cẩn thận.
Khi nào nên dùng?	Bài toán tổng đoạn, cập nhật điểm, đếm tần suất. Khi tốc độ code và bộ nhớ là ưu tiên.	Bài toán phức tạp (min/max trên đoạn), cập nhật đoạn. Khi sự linh hoạt là quan trọng nhất.

3. BIT Được Dùng Trong Các Bài Toán Nào?

Hai thao tác lõi của BIT

update(i, Δ): “rót” một thay đổi tại vị trí i lên các nút tổ tiên theo bước nhảy i += i & -i.
query(i): lấy tổng hợp tiền tố (prefix) từ 1..i bằng cách đi lùi i -= i & -i.

BIT luôn lưu kết quả gộp cho các đoạn có độ dài là lũy thừa của 2: [i - LSB(i) + 1, i]. Vì thế, để ghép nhiều đoạn lại thành một prefix, phép gộp phải “hợp tác” tốt.

Điều kiện đại số cho phép toán “gộp”

Gọi phép gộp là ⊗, phần tử đơn vị là e, và (nếu có) nghịch đảo là inv(·):

Bắt buộc: ⊗ kết hợp (associative) và có đơn vị: (a ⊗ b) ⊗ c = a ⊗ (b ⊗ c), a ⊗ e = e ⊗ a = a. → Lý do: query(i) ghép nhiều “khối” tiền tố theo thứ tự bất kỳ mà vẫn ra đúng.
Nếu muốn lấy đoạn [l, r] từ hai prefix: cần nghịch đảo để tách phần thừa: range(l, r) = prefix(r) ⊗ inv(prefix(l-1)). → Không có nghịch đảo thì không suy ra được kết quả đoạn từ hai prefix.

Nói ngắn gọn:

Với đủ nghịch đảo → làm được point update + range query (lấy từ 2 prefix).
Chỉ có tính kết hợp (không nghịch đảo) → chỉ đáng tin cho prefix query.

Những phép toán cụ thể dùng được với BIT

Phép gộp trên mảng	Đơn vị	Có nghịch?	Làm tốt với BIT	Ghi chú
Cộng ( + ) trên số nguyên/thực	0	Có (−)	Point update + prefix/range sum	Phổ biến nhất
XOR	0	Có (XOR chính nó)	Point update + prefix/range XOR	Tương tự cộng
Nhân (không 0) hoặc nhân mod p	1	Có (÷ hoặc nhân với nghịch đảo mod)	nếu tránh 0	Cẩn thận tràn số/0
Cộng mod M	0	Có (− mod M)		Chuẩn trong bài mod
Min / Max	+∞ / −∞	Không	Chỉ prefix đáng tin	Không tách được [l,r] từ 2 prefix. Cho phép nếu update đơn điệu (chỉ tăng với max/chỉ giảm với min)
AND / OR bit	all-1 / 0	Không	Chỉ prefix	Hợp khi update đơn điệu (OR chỉ bật bit, AND chỉ tắt bit)
GCD / LCM	0 / 1	Không	Chỉ prefix	Không có nghịch chung nên không lấy được [l,r]

4. Tổng Kết

Chúng ta đã đi từ một bài toán đơn giản, khám phá giới hạn của các giải pháp ban đầu, và tìm ra vẻ đẹp của Cây Chỉ Số Nhị Phân (BIT).

Khi nào nên dùng BIT?

Cần tính tổng đoạn hoặc các phép toán có nghịch đảo.
Bài toán có cả truy vấn và cập nhật điểm xen kẽ.
Cần code nhanh, ngắn gọn và tiết kiệm bộ nhớ.

BIT là một ví dụ tuyệt vời cho tư duy thuật toán: tìm kiếm sự cân bằng và tận dụng các tính chất toán học để tạo ra giải pháp hiệu quả. Một khi đã hiểu sâu, nó sẽ trở thành một công cụ không thể thiếu trong kho vũ khí của anh em.

Hẹn gặp lại anh em trong phần 2 với BIT!

Data Structures DSA Binary Indexed Tree Fenwick Tree BIT