Cấu trúc và thuật toán Advanced Encryption Standard (Chuẩn mã hóa nâng cao)

Mục tiêu

Nhân tiện việc tuần vừa rồi mình có phải học và thuyết trình về chuẩn mã hóa nâng cao (AES), hôm nay mình muốn viết blog này để giúp mình tổng hợp lại kiến thức cũng như giúp các bạn hiểu hơn về cấu trúc và thuật toán của AES!

Tổng quan về Advanced Encryption Standard (Chuẩn mã hóa nâng cao)

AES là một mã khối, nhưng khác với các mã khối khác được biết đến trước đây (DES, IDEA,…), dữ liệu trong AES không được biểu diễn dưới dạng một mảng các byte hay các bit mà được biểu diễn dưới dạng một ma trận 4xNb và được gọi là mảng trạng thái (state). Trong đó, đối với AES, Nb luôn có giá trị bằng 4. Trong khi thuật toán Rijndael hỗ trợ ba giá trị của Nb là 4, 6, 8 tương ứng với kích thước khối 128, 192 và 256 bit Dữ liệu đầu vào được đọc vào ma trận state theo từng cột, theo thứ tự từ trên xuống dưới, từ trái qua phải. Dữ liệu đầu ra được đọc từ ma trận cũng theo quy tắc trên.

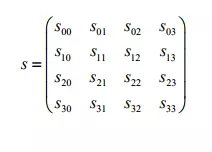
Khóa vòng trong AES cũng được biểu diễn hoàn toàn tương tự như cách biểu diễn dữ liệu. Tuy nhiên, tùy vào kích thước khóa mà số cột của ma trận khóa vòng Nk sẽ khác nhau. Cụ thể, Nk nhận các giá trị 4, 6, 8 tương ứng với các kích thước khóa là 128, 192 và 256 bit. Đây chính là điểm mạnh của thuật toán AES trong vấn đề mở rộng khóa.

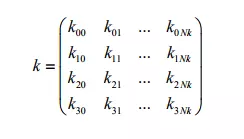
Số vòng lặp ký hiệu là Nr, phụ thuộc vào hai đại lượng Nb và Nk. Vì Nb trong AES có giá trị cố định nên Nr chỉ phụ thuộc vào Nk. Giá trị của Nr tương ứng với ba giá trị của Nk là Nr = 10, 12, 14. Cụ thể, giá trị Nr được xác định bởi

Khái niệm từ (Word) trong AES

Bốn byte trên mỗi cột trong mảng trạng thái state tạo thành 1 từ 32 bit, trong đó số thứ tự của hàng r (0≤r<4) cho biết chỉ số của bốn byte trong mỗi từ. Từ định nghĩa state ở trên có thể coi state là mảng một chiều chứa các từ 32 bit

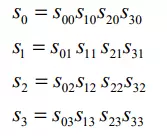
Tương tự như đối với mảng khóa cũng có thể biểu diễn thành mảng một chiều chứa các từ 32 bit như công thức dưới đây với số lượng từ khóa phụ thuộc vào Nk (Nk=4, 6, 8).

Thuật toán của AES

Thuật toán AES khá phức tạp, được mô tả khái quát gồm 3 bước như sau:

• 1 Vòng khởi tạo chỉ gồm phép AddRoundKey
• Nr -1 Vòng lặp gồm 4 phép biển đổi lần lượt: SubBytes, ShiftRows, MixColumns, AddRoundKey.
• 1 Vòng cuối gồm các phép biến đổi giống vòng lặp và không có phép MixColumns.

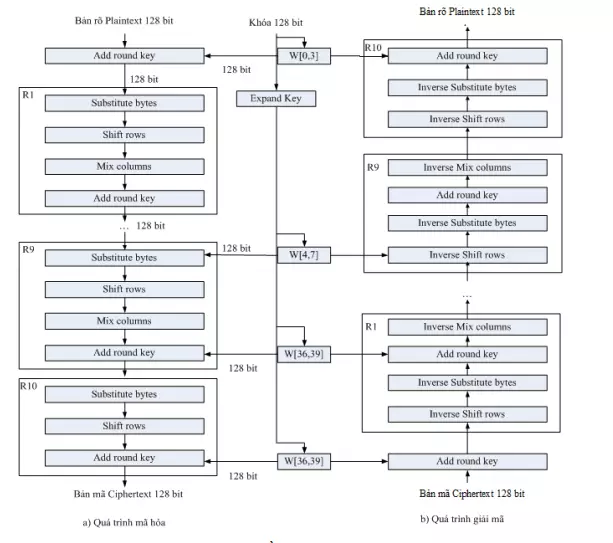
Khái quát: 1. Mở rộng khóa - Các khóa phụ dùng trong các vòng lặp được sinh ra từ khóa chính AES sử dụng thủ tục sinh khóa Rijndael. 2. InitialRound - AddRoundKey— Mỗi byte trong state được kết hợp với khóa phụ sử dụng XOR 3. Rounds - SubBytes—bước thay thế phi tuyến tính, trong đó mỗi byte trong state được thay thế bằng một byte khác sử dụng bảng tham chiếu - ShiftRows—bước đổi chỗ, trong đó mỗi dòng trong state được dịch một số bước theo chu kỳ - MixColumns—trộn các cột trong state, kết hợp 4 bytes trong mỗi cột - AddRoundKey 4. Final Round (không MixColumns) - SubBytes - ShiftRows - AddRoundKey.

Thuật toán giải mã khá giống với thuật toán mã hóa về mặt cấu trúc nhưng 4 hàm sử dụng là 4 hàm ngược của quá trình mã hóa. Riêng đối với cấu trúc giải mã trong AES gồm 2 chế độ giải mã: - Ở cấu trúc giải mã ngược, gồm vòng khởi tạo, Nr-1 vòng lặp và vòng kết thúc. Trong đó vòng khởi tạo chỉ có phép biến đổi AddRounKey, vòng lặp gồm lần lượt 4 phép biến đổi chính: InvShiftRows, InvSubBytes, AddRounKey, InvMixColumns; vòng kết thúc khác với vòng lặp chính ở chỗ không có phép InvMixColumns. - Ngược lại với cấu trúc giải mã ngược là cấu trúc giải mã xuôi, việc ngược lại thể hiện ở điểm: trong cấu trúc giải mã xuôi việc sắp xếp các phép biến đổi ngược giống hệt với cấu trúc mã hóa, cụ thể bao gồm: vòng khởi tạo, Nr-1 vòng lặp và vòng kết thúc. Trong đó vòng khởi là phép AddRounKey; ở vòng lặp thứ tự các phép biến đổi ngược lần lượt là: InvSubBytes, InvShiftRows, InvMixColumns, AddRounKey; vòng kết thúc giống vòng lặp nhưng được lược bỏ phép InvMixColumns. Một điểm khác biệt nữa trong hai cấu trúc giải mã ngược và giải mã xuôi đó là: Trong giải mã ngược khóa vòng giải mã chính là khóa vòng mã hóa với thứ tự đảo ngược. Còn trong giải mã xuôi thì khóa giải mã ngoài việc đảo ngược thứ tự khóa vòng mã hóa còn phải thực hiện phép InvMixColumns đối với các khóa vòng của vòng lặp giải mã.

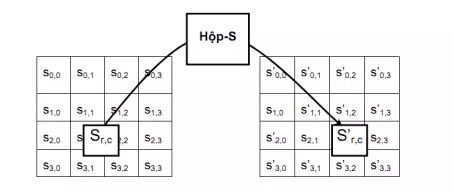
SubBytes và InvSubBytes

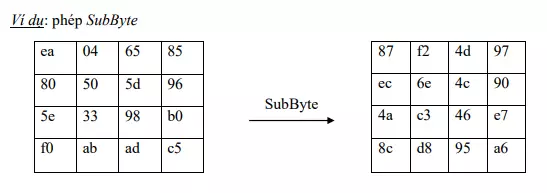
Phép biến đổi SubBytes: Là phép thay thế byte phi tuyến tính, ở phép thay thế này nó tác động độc lập đến từng byte trong trạng thái hiện hành. Phép biến đổi SubBytes được thực hiện bằng cách tra cứu bảng thay thế (S-box) với tham số đầu vào là các byte trong bảng trạng thái. S-box được xây dựng như sau: Bước 1: Điền các con số từ 0 đến 255 vào bảng theo từng hàng. Vậy hàng 0 gồm các con số {00}, {01}, …{0F} (thập lục phân). Hàng 1 gồm các con số {10}, {11},…, {1F}. Điều này có nghĩa là tại hàng x cột y có giá trị {xy}. Bước 2: Thay thế mỗi byte trong bảng bằng giá trị nghịch đảo trong trường GF(28 ). Quy ước nghịch đảo của {00} cũng là {00}. Bước 3: Mỗi byte trong ma trận state được thay thế bởi 1 byte trong Rijndael S-box, hay bij = S(aij).

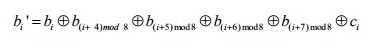
trong đó, 0 ≤ i ≤8 là bit thứ i của byte b tương ứng và ci là bit thứ thứ i của byte c với giá trị {63} hay {01100011}.

Trong đó phép cộng thực hiện như phép XOR. Bảng sau trình bày nội dung bảng S-box sau khi tính toán.

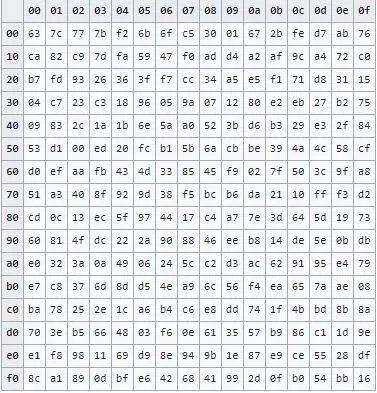
Phép biến đổi ngược InvSubBytes: là phép thay thế biến đổi ngược với SubBytes. Là một phép thay thế byte, các byte thay thế được thực hiện bằng cách tra bảng thay thế ngược IS. Bảng thay thế ngược IS này được xây dựng như sau: Trước tiên, cũng phải xây dựng một bảng Inverse SubBytes (IS- box). Nghĩa là nếu với đầu vào {95}, S-box cho ra kết quả {2A}, thì với đầu vào là {2A}, IS sẽ cho ra lại kết quả {95}. Việc xây dựng hộp IS cũng giống như xây dựng S-box tại bước 1 và bước 2. Tại bước 3, IS thực hiện phép thay thế sau:

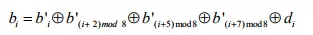
Với di là bit thứ i của số {05} tức d7 d6 d0 = 00000101.

Bảng sau trình bày nội dung bảng thay thế ngược IS sau khi tính toán.

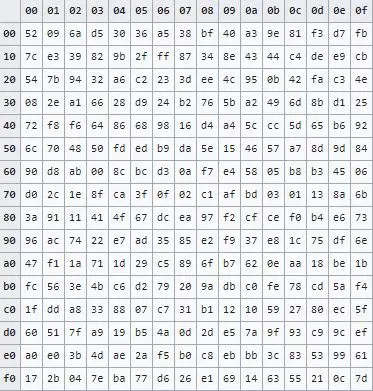
Như vậy: phép biến đổi InvSubBytes thực hiện như sau: Mỗi byte trong ma trận state S, dưới dạng thập lục phân là {xy}, được thay thế bằng giá trị trong bảng IS tại dòng x cột y.

Mục đích của phép biến đổi SubBytes: S-box dùng để chống lại hình thức tấn công thám mã vi sai và thám mã tuyến tính. Giữa input và output của phép Substitute bytes không thể mô tả bằng một công thức toán đơn giản

ShiftRows và InvShiftRows

Phép biến đổi ShiftRows: Thao tác ShiftRows thực hiện hoán vị các byte trong ma trận state theo cách thức sau:

• Dòng thứ nhất giữ nguyên
• Dòng thứ 2 dịch vòng trái 1 byte
• Dòng thứ 3 dịch vòng trái 2 byte
• Dòng thứ 4 dịch vòng trái 3 byte

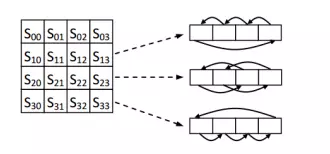
Phép biến đổi InvShiftRows: Phép biến đổi InvShiftRows thực hiện ngược lại với phép ShiftRows, nghĩa là:

• Dòng thứ nhất giữ nguyên
• Dòng thứ 2 dịch vòng phải 1 byte
• Dòng thứ 3 dịch vòng phải 2 byte
• Dòng thứ 4 dịch vòng phải 3 byte Mục đích của ShiftRows: Xáo trộn các byte để tạo các cột khác nhau trước khi sử dụng cột cho thao tác MixColumns.

MixColumns và InvMixColumns

Phép biến đổi MixColumns: Phép biến đổi MixColumns thực hiện biến đổi độc lập từng cột trong ma trận state bằng một phép nhân đa thức. Mỗi cột của state đươc coi là biểu diễn của một đa thức f(x) trong GF(2^8) như vậy phép biến đổi MixColumns chính là phép nhân theo modulo với x^4+1 với một đa thức cố định định nghĩa như sau:

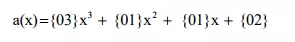
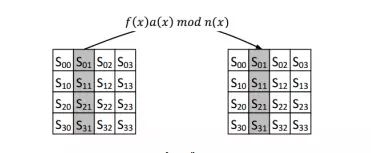
Phép nhân đa thức trên có thể biểu diễn dưới dạng phép nhân ma trận như sau

Ví dụ về phép MixColumns:

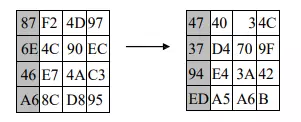
Phép biến đổi ngược InvMixColumns: Là phép biến đổi ngược với phép biến đổi MixColumns. InvMixColumns cũng thực hiện thao tác theo từng cột của trạng thái, xem mỗi cột như một đa thức bậc 3 gồm 4 hạng tử trên trường GF(2^8). Các cột của phép InvMixColumns được nhân theo modulo ( x^4 + 1 ) với đa thức nghịch đảo a(x) chính là đa thức a^-1(x) được định nghĩa:

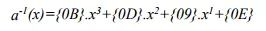
Như vậy phép InvMixColumns cũng được biểu diễn tương đương với phép nhân ma trận sau

Mục đích của MixColumns: Việc coi mỗi cột là một đa thức bậc 3, rồi nhân mỗi cột với đa thức a(x) sau đó modulo ( x4 1 ) đã làm cho mỗi byte trong cột kết quả đều phụ thuộc vào bốn byte trong cột ban đầu. Thao tác MixColumns kết hợp với ShiftRows đảm bảo rằng sau một vài vòng biến đổi, 128 bit trong kết quả đều phụ thuộc vào tất cả 128 bit ban đầu. Điều này tạo ra tính khuếch tán (diffusion) cần thiết cho mã hóa.

AddRoundKey

Trong thao tác AddRoundKey, 128 bit của ma trận state sẽ được XOR với 128 bit của khóa con của từng vòng. Vì sử dụng phép XOR nên phép biến đổi ngược của AddRoundKey trong cấu trúc giải mã cũng chính là AddRoundKey. Việc kết hợp với khóa bí mật tạo ra tính làm rối (confusion) của mã hóa. Sự phức tạp của thao tác mở rộng khóa (KeySchedule) giúp gia tăng tính làm rối này.

Mở rộng khóa (ExpandKey )

ExpandKey là thao tác tạo lược đồ khóa hay mở rộng khóa, tạo ra Nr+1 khóa vòng từ khóa chính K, mỗi khóa vòng gồm Nb từ 32 bit, trong đó đối với AES thì Nb = 4, còn Nr được xác định theo. Các phép biến đổi để tạo khóa vòng trong ExpandKey là khác nhau đối với các giá trị khác nhau của kích thước khóa K. Sau đây là việc mở rộng khóa đối với khóa mã 128 bit

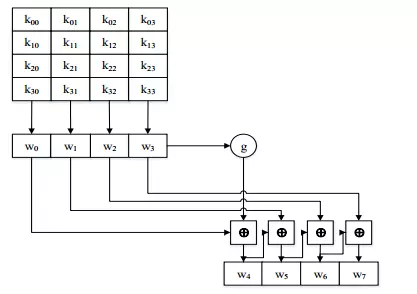
Trong thao tác mở rộng khóa với khóa mã 128 bit có đầu vào là 16 byte (4 word) của khóa mã, và sinh ra một mảng khóa vòng (Nr+1)x4=44 từ (word) hay 176 byte. 44 word này được sử dụng cho 11 vòng mã hóa của AES, mỗi vòng dùng 4 word. Từ bốn word đầu vào w0w1w2w3, trong lần lặp đầu tiên thao tác ExpandKey sinh ra bốn word w4w5w6w7, lần lặp thứ 2 từ w4w5w6w7 sinh ra w8w9w10w11 , cứ như thế cho đến lần lặp thứ 10 (tùy thuộc chiều dài khóa) sinh ra bốn word cuối cùng w40w41w42w43 như hình vẽ

Mục đích của ExpandKey: dùng để chống lại known-plaintext attack

• Biết một số bit của khóa hay khóa con cũng không thể tính các bit còn lại.
• Không thể tính ngược: biết một khóa con cũng không thể tính lại các khóa con trước đó.
• Tính khuếch tán: một bit của khóa chính tác động lên tất cả các bit của các khóa con.

Kết luận

Phương pháp mã hóa AES đơn giản, có thể thực hiện hiệu quả trên các vi xử lý 8 bit (dùng trong smartcard) cũng như trên các vi xử lý 32 bit, chỉ dùng phép XOR và phép Shift bit. Đây chính là yếu tố cơ bản để phương pháp này được chọn làm chuẩn mã hóa của Hoa Kỳ.