Cấu trúc dữ liệu yếu lược: Những gì mọi developer cần biết

Trong Kinh Thánh, Jesus Christ từng nói:

Vậy ai nghe những lời Thầy nói đây mà đem ra thực hành, thì ví được như người khôn xây nhà trên đá. Dù mưa sa, nước cuốn, hay bão táp ập vào, nhà ấy cũng không sụp đổ, vì đã xây trên nền đá. Matthew 7:24-25

Trong công việc lập trình cũng vậy, nếu muốn đi xa, đào sâu, thì chúng ta nên xây dựng một kiến thức nền tảng vững vàng. Kẻo đôi lúc đọc bài viết chuyên sâu, có đôi ba thuật ngữ cơ bản thì lúc ấy không hiểu, lại phải tốn thời gian tìm kiếm tiếp.

Đó là lý do bài viết này ra đời.

First things first

Again, mình là Kiên - một Christian, và cũng là một developer thích viết. Đây là bài viết nằm trong chuỗi series backend nâng cao. Mục đích của chuỗi bài này trước hết là động lực cho mình tìm tòi và học hỏi sâu hơn về công việc chúng ta đang làm; sau đó là để chia sẻ cho cộng đồng, "nhân bản kiến thức", để có thể giúp được cho ai đó đang cần tìm những kiến thức này (giống mình trước đây).

Bài viết này có mục đích để cung cấp những khái niệm cơ bản về cấu trúc dữ liệu (data structure), những điều này có thể bạn chưa được học; hoặc đa phần có thể đã học nhưng lại vứt ra sau đầu rồi; hoặc chỉ là ôn lại thôi, giúp việc bạn đọc sách, đọc tài liệu chuyên môn được "mượt" hơn.

☕ Như thông lệ, bài này khá dài. Hãy ngồi xuống nhâm nhi ly bánh, ăn miếng cafe rồi thong thả đọc.

Cấu trúc dữ liệu là gì?

Trong khoa học máy tính, cấu trúc dữ liệu là phương pháp tổ chức (organize) và lưu trữ (store) dữ liệu trong chương trình máy tính sao cho có thể dễ dàng truy cập và sử dụng chúng một cách hiệu quả.

Độ phức tạp thuật toán

Khoan, bài viết về cấu trúc dữ liệu mà, tự dưng lôi thuật toán ra chi vậy?

Có lý do cả nha, vì khi chọn một cấu trúc dữ liệu để sử dụng, ta cần xem xét vài điểm đặc trưng của nó, và độ phức tạp thuật toán là không thể bỏ qua.

Có 2 loại độ phức tạp:

• Độ phức tạp thời gian - Time complexity: Là khoảng thời gian mà thuật toán cần để hoàn thành phép tính với một độ dài input N.
• Độ phức tạp về không gian - Space complexity: Là số lượng bộ nhớ mà thuật toán cần.

Thường thì ta chỉ nhắc tới Time complexity, vì các hệ thống bây giờ RAM nhiều, rơi vãi đầy đất rồi 😊.

Độ phức tạp lại được chia làm 3 trường hợp: Best case; average case; và worst case, tương tự cho trường hợp tốt nhất, trung bình và tệ nhất tùy thuộc vào dữ liệu input. Thế nhưng thông thường con số của worst case sẽ được lấy làm chuẩn khi nói về độ phức tạp của một thuật toán nào đó.

Để trình bày độ phức tạp thuật toán, ta có thể dùng BigO notation, là cái chữ O to to đó mọi người.

Cách tính độ phức tạp thuật toán

Độ phức tạp càng thấp, thì thuật toán càng hiệu quả. Chúng ta sẽ tính độ phức tạp dựa trên độ dài N của tham số đầu vào.

Có các phương pháp khác nhau để tính độ phức tạp, nhưng ta có thể dựa vào số vòng lặp để ước lượng một cách khá chính xác theo Big O notation.

📌 Đầu tiên ta cần phân biệt 1 chút vòng lặp và lần lặp.

• Vòng lặp: mình sẽ nói tới 1 vòng for (for từ i tới N).
• Lần lặp: sẽ là 1 lần chạy (iteration) của vòng for đó (1 giá trị của i). Một vòng lặp thường chứa nhiều lần lặp.

• Nếu function mất 1 số lần lặp nhất định (không đổi theo input) để hoàn thành, thì đó là O(1). O(20), O(5000), O(90000) …. đều quy về O(1)
• Nếu mất 1 vòng lặp với N lần, nó sẽ là O(n), nếu mất 2 vòng lặp (không lồng nhau) sẽ là O(2n), 3 thì sẽ là O(3n)… đều quy về O(n).
• Nếu function mất 2 vòng lặp, nhưng nó lồng nhau, thì sẽ là O(n^2).
• …

Vài giá trị độ phức tạp phổ biến, mình tham khảo từ bài viết này, cách trình bày khá dễ hiểu:

Big O	Rank	Ý nghĩa
$O(1)$	😎	Tốc độ không phụ thuộc vào độ lớn dữ liệu, tâm bất biến giữa lòng đời vạn biến.
$O(log n)$	😁	Nếu dữ liệu tăng gấp 10 lần thì tốn gấp đôi thời gian
$O(n)$	😕	Nếu dữ liệu tăng gấp 10 lần thì thời gian tốn gấp 10 lần
$O(n \log n)$	😖	Nếu dữ liệu tăng gấp 10 lần thì tốn gấp 20 lần thời gian
$O(n^2)$	😫	Nếu dữ liệu tăng gấp 10 lần thì thời gian tăng gấp 100 lần
$O(2^n)$	😱	Dữ liệu tăng gấp đôi là đủ chết rồi!!!

Nhìn 2 hình sau để thấy cách fancy hơn (lấy từ bigOcheatsheet):

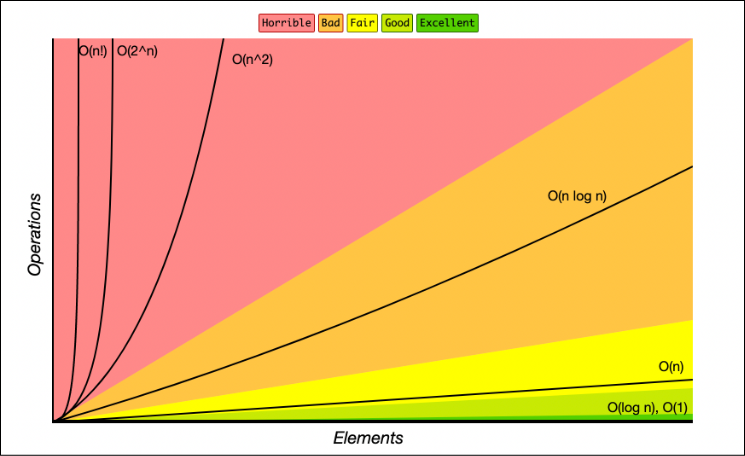
Độ phức tạp ở những kiểu dữ liệu phổ biến:

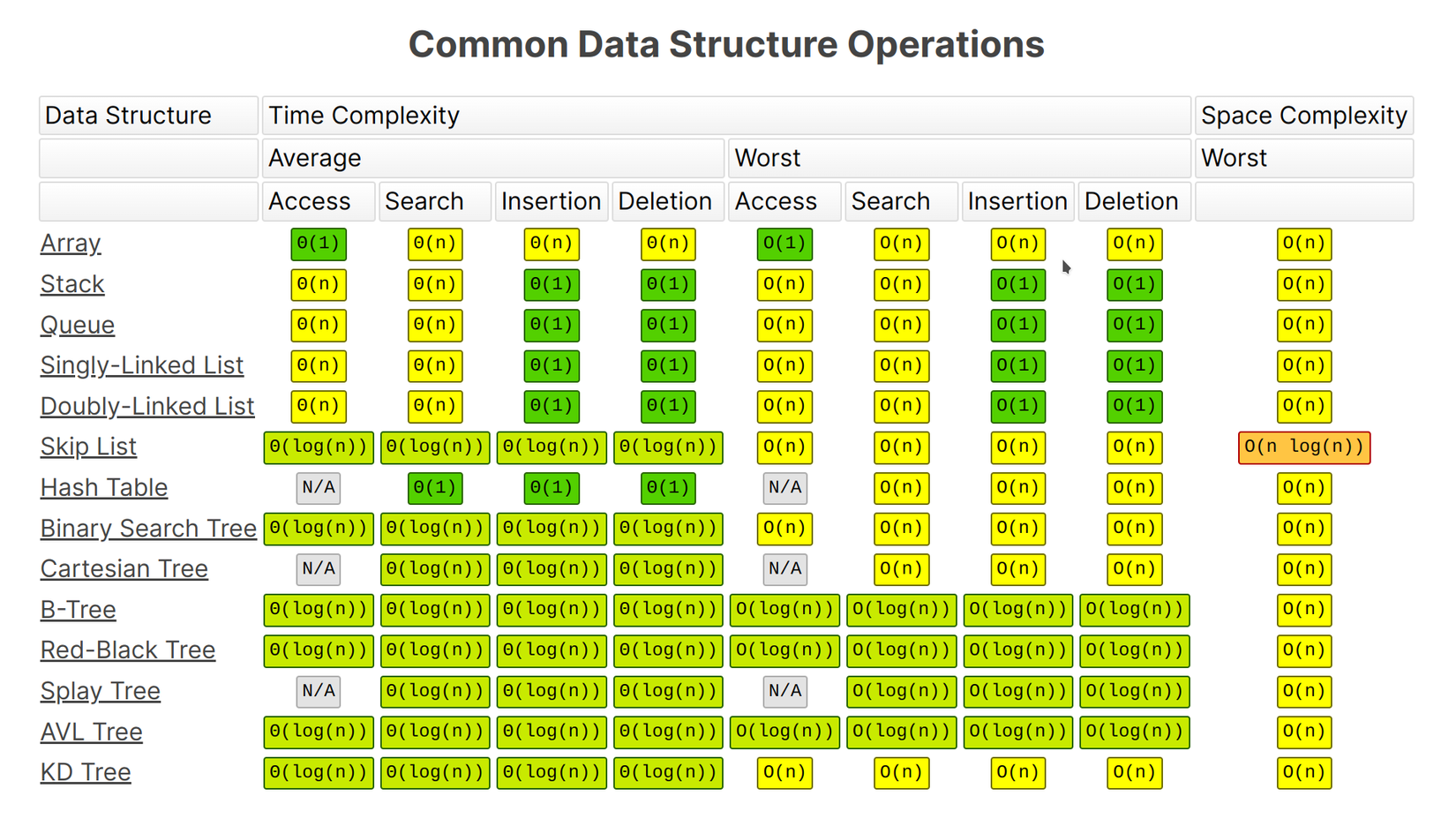
Bộ nhớ Stack và Heap

Đây là 2 khái niệm về quản lý bộ nhớ (memory management) được dùng rất nhiều khi chúng ta làm việc, bởi vì nó ảnh hưởng trực tiếp tới hiệu năng của phần mềm.

Khi nhắc tới Stack và Heap là người ta đang nói tới 2 vùng nhớ để lưu dữ liệu cho chương trình trong bộ nhớ RAM.

Chắc hẳn ai ai cũng sẽ biết rằng truy cập dữ liệu ở stack thì sẽ nhanh hơn là heap, nhưng liệu bạn đã hiểu tường tận nó hoạt động ra sao và tại sao lại nơi thì chậm, chốn thì lại nhanh chưa?

Stack

Stack là một cấu trúc dữ liệu dạng ngăn xếp, có tính chất LIFO (Last In First Out - vào trước ra sau). Giống như bạn xếp một chồng đĩa CD vào 1 cái cọc vậy, lúc bạn muốn lấy đĩa ra thì thứ tự sẽ phải ngược lại lúc bạn đẩy vào.

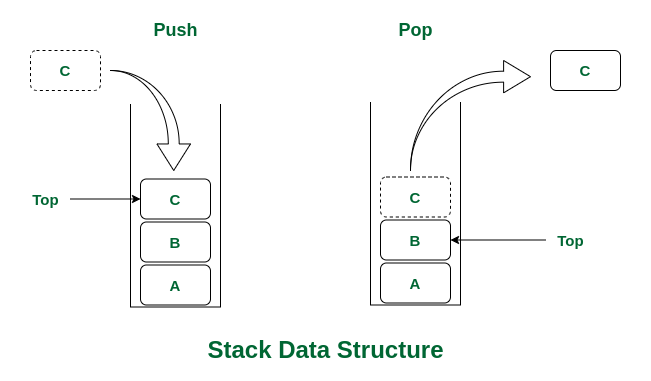
Ở phần này thì Stack vừa là cấu trúc dữ liệu, vừa được coi như là một vùng nhớ để so sánh với Heap các bạn nhé.

Heap

Heap này không phải là một cấu trúc dữ liệu, mà là một vùng nhớ trên RAM, và vì nó được cấp phát lộn xộn hơn Stack nên việc đọc sẽ luôn luôn là sequence scan (quét hết) để lấy dữ liệu, do vậy nó chậm.

Cách các chương trình lấy bộ nhớ từ Stack và Heap

Stack có ưu điểm là nhanh, vậy tại sao các chương trình không lưu toàn bộ giá trị vào stack, mà lại lưu thêm vào Heap làm chi cho nó khộ?

Hãy xem cách stack hoạt động.

Stack sẽ cấp phát bộ nhớ cho từng function, mỗi vùng nhớ của function được gọi là 1 frame, và khi function đó kết thúc, frame này được bỏ đi (lấy ra khỏi stack) và trở về frame trước đó (function cha). Ta gọi nó là call stack.

Bởi vì dữ liệu đi theo frame và truyền đi truyền lại theo từng function như vậy, nên chương trình runtime có thể dễ dàng truy xuất dữ liệu với frame cụ thể, do đó stack có tốc độ truy cập nhanh hơn heap.

Nhưng cũng bởi lẽ đó nên stack sẽ không sử dụng được trong 2 trường hợp sau:

• Giữ 1 giá trị lâu dài (kể cả khi đóng function tạo nó).
• Muốn cấp phát động bộ nhớ cho biến (ví dụ như Slice trong go, tham khảo bài mình viết: Tất tần tật về Slice)

Có phải bạn tưởng tượng Stack và Heap như thế này?

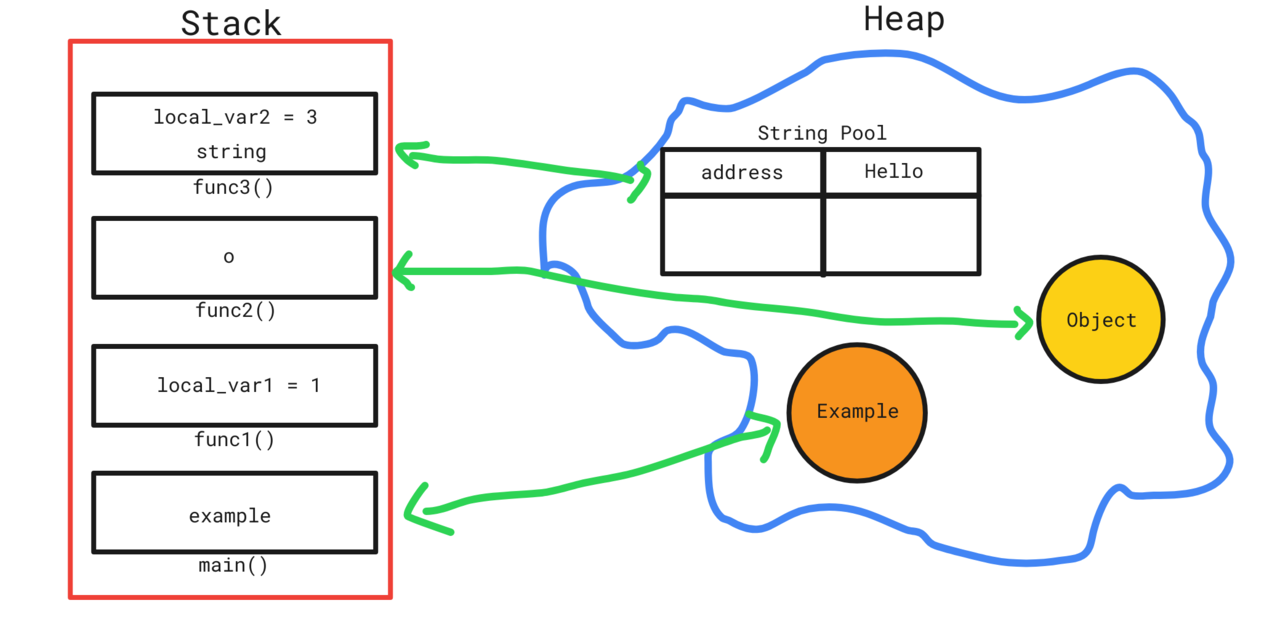
Thực tế đúng hơn là như này, chúng không nằm tách biệt, mà chỉ là vị trí và cách truy cập khác nhau mà thôi ¹:

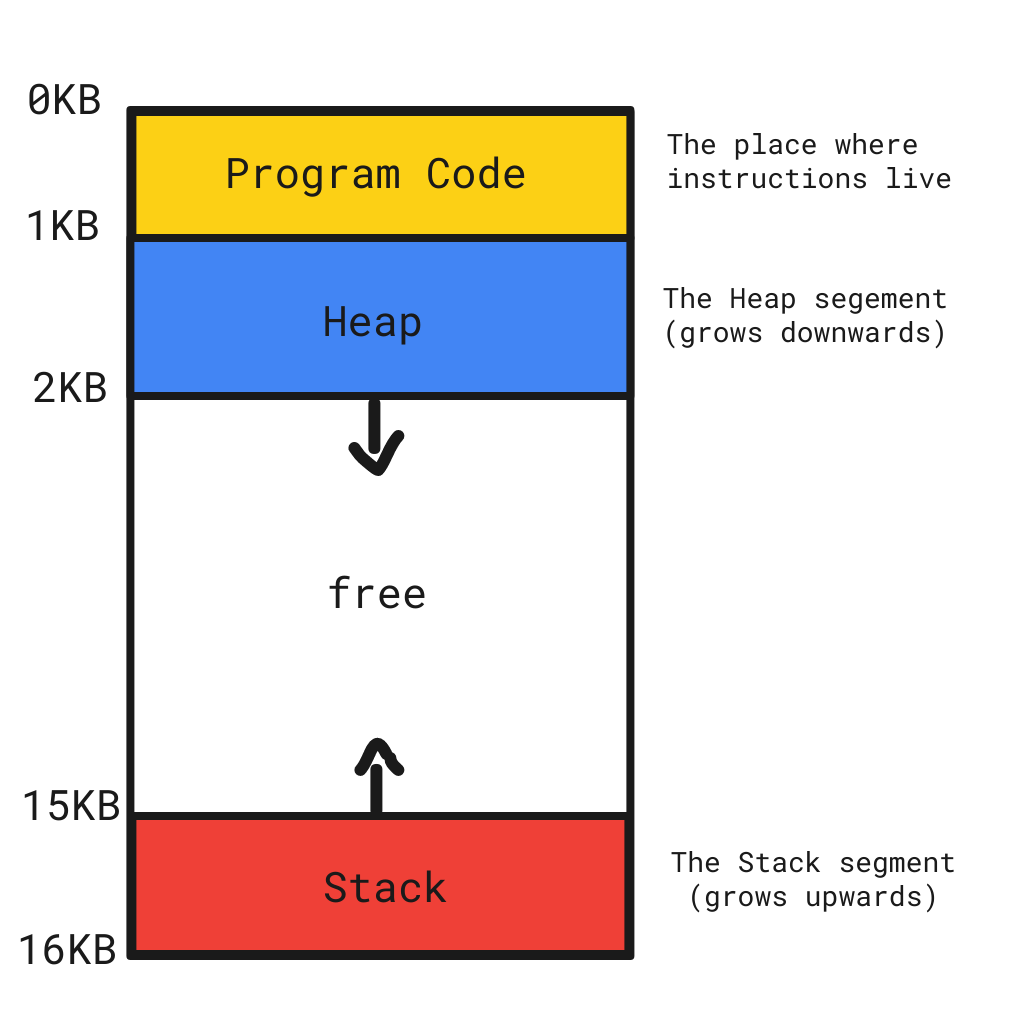
Nhìn hình trên, thì bạn có thể hình dung trường hợp các stack frame cứ tăng mãi tăng mãi, cho tới khi vượt mức bộ nhớ được quy định cho call stack ⇒ bùmmmm, lỗi stackoverflow.

Hãy hình dung Heap như một khán đài sân vận động đầy ắp ghế ngồi mà không bán vé, chỉ xếp chỗ ngồi 1 cách linh hoạt vì đang diễn ra một trận đấu đặc biệt.

• Có khán giả đi xem bóng một mình, nên người ta chỉ cần xếp cho 1 vị trí bất kì.
• Có tốp thì đi xem cùng bạn bè trong lớp, số lượng khoảng 30 người; lúc này việc tìm chỗ trống cho cả lớp có vẻ sẽ lâu hơn 1 chút, vì các bạn có nhu cầu ngồi cùng nhau trên cùng 1 dãy (đây là cách mà runtime cấp phát bộ nhớ cho Array).

Khi tìm và đã sắp xếp xong chỗ ngồi, người ta quay lại ghi vào sổ thành viên nào thuộc nhóm nào, đang ngồi ở ghế số mấy (địa chỉ ô nhớ).

Nhưng người xếp chỗ ngồi cũng không biết được chính xác khán giả sẽ rời ghế đi về vào lúc nào cả, do đó người ta cần một người thi thoảng lại đi kiểm tra, xem ghế nào trống thì sẽ báo về cho người quản lý cập nhật vào sổ. ⇒ Đây là Garbage Collector (GC).

Các cấu trúc dữ liệu phổ biến

Ngoài Stack được sử dụng rộng rãi ở level runtime để cấp phát bộ nhớ như vậy, thì còn những kiểu cấu trúc dữ liệu khác, được áp dụng cho nhiều trường hợp cụ thể chuyên biệt.

Array

Array - mảng, chắc hẳn là một kiểu dữ liệu quá "fundamental" rồi. Với complexity để truy cập một phần tử là O(1), cho nên array được sử dụng rất nhiều, không cần bàn cãi.

Để có thể truy cập nhanh như vậy, thì các phần tử của array sẽ nằm sát nhau trong bộ nhớ (có thể là heap hoặc stack tùy ngôn ngữ).

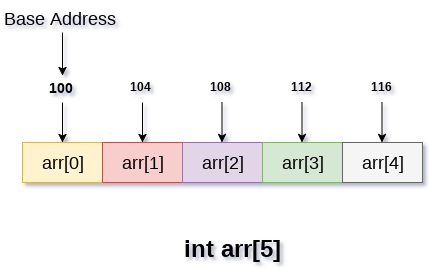
Điểm hạn chế của Array là bạn không thể thay đổi kích thước của nó, bạn chỉ có thể tạo 1 array mới với size lớn hơn, và copy dữ liệu cũ qua mà thôi. Do đó việc thêm mới hoặc xóa phần tử trở nên tốn thời gian: Là O(n) vì phải loop hết cả mảng để copy.

Đó cũng là cách hoạt động "behind the scene" của mấy kiểu dữ liệu dạng List như ArrayList trong Java, Slice trong Go, Array trong Javascript…

📎 Tham khảo: Slice trong Go: Tất tần tật, và những điều có thể bạn chưa biết

Bình thường, để tìm một giá trị có nằm trong mảng hay không, ta phải thực hiện một phép tìm kiếm tuyến tính (linear search), tức là duyệt hết từ đầu mảng tới cuối mảng - O(n).

Nhưng nếu dữ liệu của mảng đã được sắp xếp, thì việc tìm kiếm sẽ dễ dàng hơn, ta có phép tìm kiếm nhị phân (binary search), đỡ tốn thời gian hơn - O(logn).

Linked List

Linked list là một sự thay thế cho Array, khi nó khắc phục được điểm yếu của Array chính là tốc độ thêm mới và xóa phần tử chậm.

Linked list về cơ bản sẽ để cho các phần tử lưu vị trí của phần tử tiếp theo (hoặc có thêm phần tử trước đó). Có vài loại linked list là Singly (chỉ lưu ref tới phần tử kế tiếp) hay Doubly (lưu cả phần tử trước và sau) và Circurlar (nối đuôi).

Nhìn hình sau:

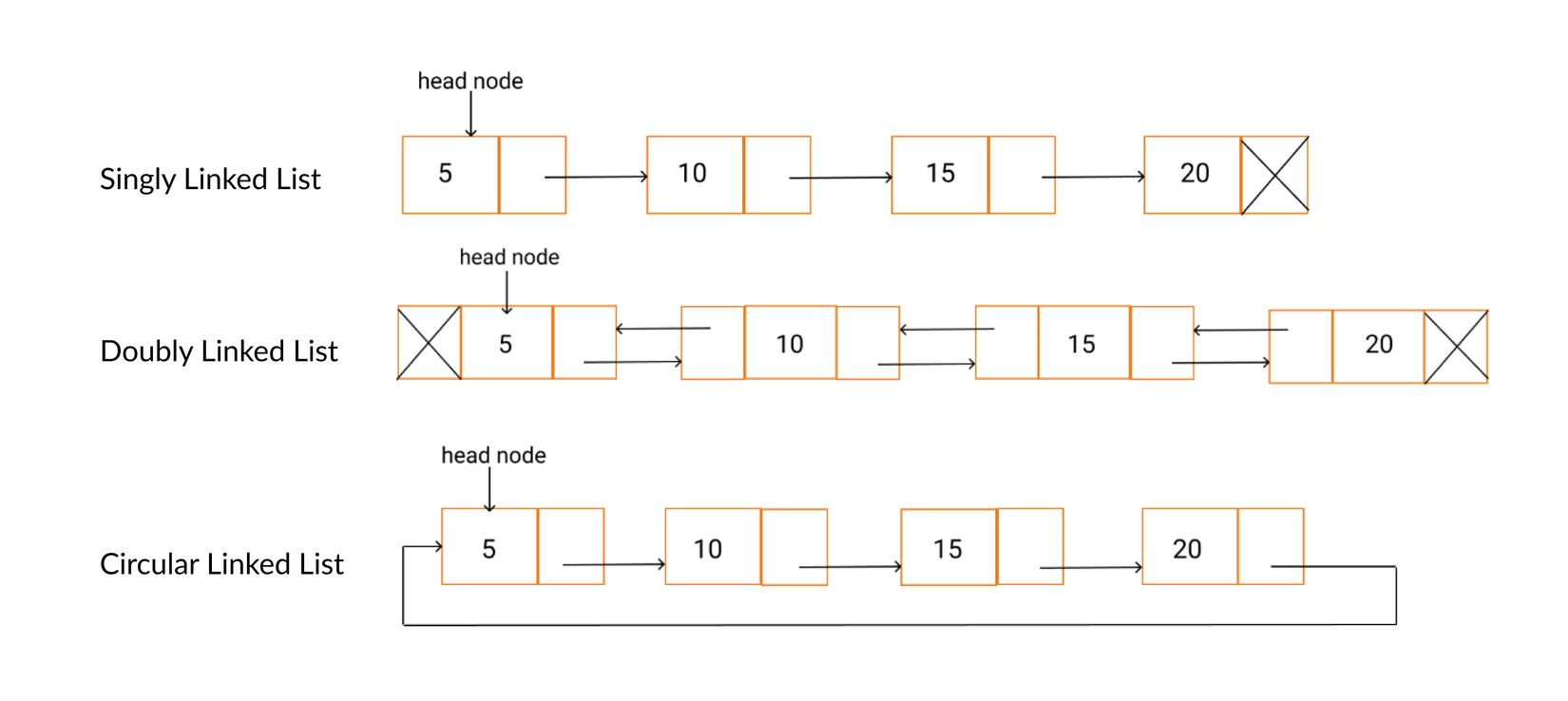
Do việc phần tử lưu luôn địa chỉ của phần tử kế tiếp/ liền trước, time complexity lúc chèn, xóa phần tử là O(1). Việc xóa phần tử chỉ đơn giản là đổi liên kết tới phần tử kế tiếp là xong. Do vậy, linked list cũng chỉ có thể được lưu trên heap.

Túm váy lại 1 chút:

Ưu điểm của Linked list:

• Kích thước không cố định như array
• Thêm, xóa phần tử nhanh

Nhược điểm:

• Tốn bộ nhớ
• Iteration (đọc hết phần tử) chậm vì các phần tử nằm ở các ô nhớ rải rác trong heap.
• Muốn tìm một phần tử thì sẽ luôn phải thực hiện tìm kiếm tuyến tính.

Vậy Linked list được áp dụng ở đâu?

Linked list ngoài việc được sử dụng rộng rãi ở các ứng dụng như music player, browser thì còn được dùng trong cả các kernel hệ điều hành như Linux (xem nguồn):

struct list_head {
    struct list_head *next, *prev;
};

Linked list cũng có thể được sử dụng trong các cấu trúc dữ liệu phức tạp hơn, chẳng hạn như Map, mình sẽ đề cập ở bên dưới.

Queue

Queue (hàng đợi) cũng là một kiểu dữ liệu có cách hoạt động khá giống stack.

Nhưng Queue có cách truy xuất khác hẳn: FIFO (Vào trước ra trước).

Cả Stack và Queue được implement có thể bằng linked list hoặc array. Chúng được sử dụng rất phổ biến, một ví dụ chính là NodeJs engine, cơ chế event loop được hậu thuẫn bởi cả stack và queue.

Tree

Tree, vâng, chính là cây. Nó có cấu trúc y chang một cái cây.

Một cái cây thì sẽ có những thành phần, khái niệm:

• Node, mọi phần tử đều có thể coi là một node.
• Gốc - root node
• Node cha, node con, nốt lá, nốt anh em…

Nhìn hình sau sẽ rõ:

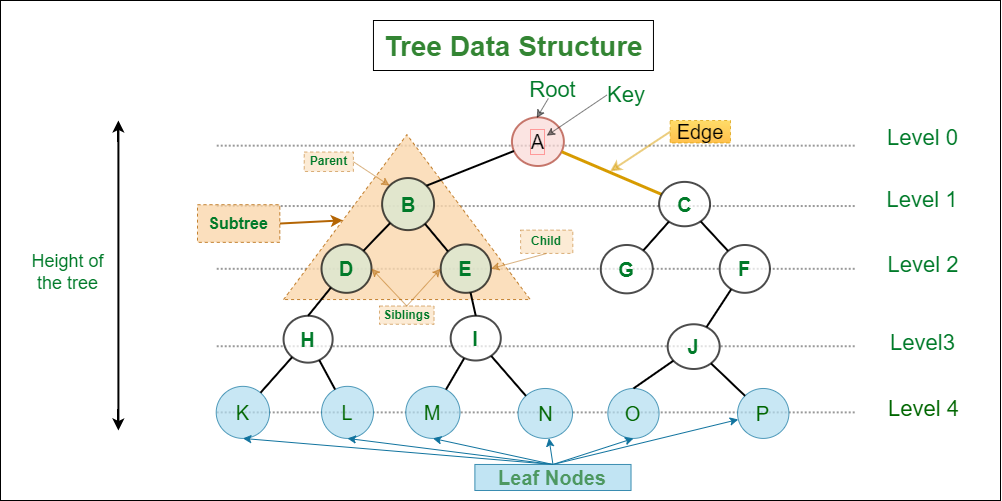
Nhưng đó chỉ là khái niệm chung cho Tree. Ở đây mình sẽ nêu vài loại Tree phổ biến và nổi tiếng nhất mà thôi.

Binary search tree: Cây nhị phân tìm kiếm (BST)

Đây là một loại binary tree - cây nhị phân, tức là mỗi node chỉ có 2 node con, trái và phải. Node con bên trái sẽ có giá trị nhỏ hơn node cha, và node bên phải sẽ có giá trị lớn hơn node cha.

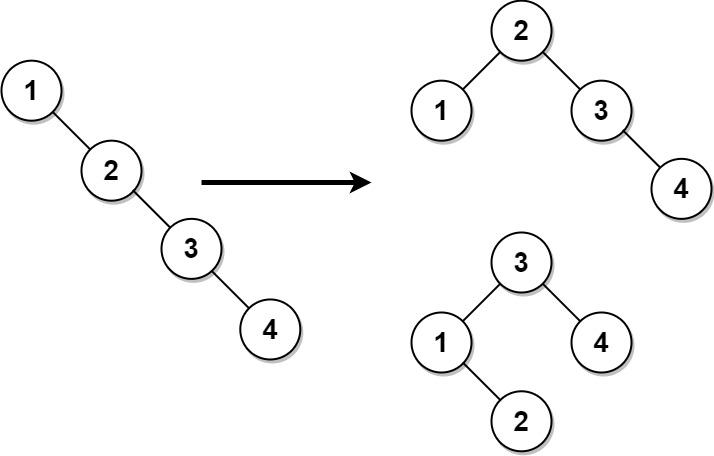
Vậy sẽ có trường hợp cây sẽ chỉ có 1 nhánh vì mình cứ chèn hoài giá trị lớn hơn hoặc bé hơn vào, lúc đó binary tree chẳng khác gì một linkedlist.

Để tránh điều này chúng ta cần cân bằng lại cây bằng vài kĩ thuật để tối ưu tốc độ, time complexity cho tree, hoặc làm luôn cây tự cân bằng mỗi lúc chèn mới giá trị vào, ta có thêm AVL tree.

BTree

Nhược điểm của Binary Tree chính là tốn bộ nhớ, khi mỗi node đều tốn không gian cho pointer tới 2 node con. Với lượng dữ liệu hàng triệu record như database thì đây sẽ là một con số rất không nên xuất hiện.

Vì vậy biến thể của BST là BTree ra đời để giải quyết vấn đề đó bằng cách một node có thể chứa nhiều key. Thay vì chỉ 1 node cha và 2 node con, ở Btree thì 1 node có n key và n+1 node con. Điều này khiến chiều cao của cây được thấp hơn BST ⇒ tiết kiệm bộ nhớ ².

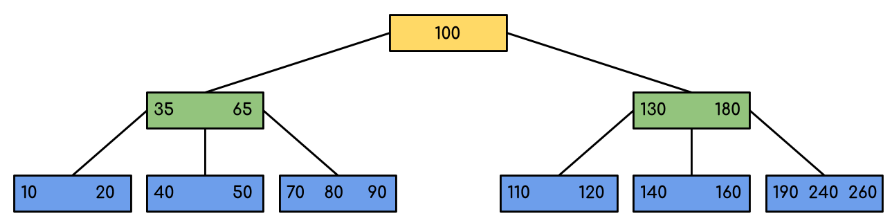
Ưu điểm của BTree:

• Tự cân bằng.
• Tiết kiệm bộ nhớ hơn.
• Time complexity cho các tác vụ luôn là O(log n).

BTree là một trong những cấu trúc được dùng để lưu index trong các database hiện nay (Mysql, postgres, MSSQL…)

Heap

Lại là heap, ông đùa tôi à?

Khoan nào, bình tĩnh.

Heap ở đây là một loại Tree chứ không phải là một vùng nhớ.

Heap là một loại Binary tree, có 2 loại Heap:

• Min heap: Node gốc luôn là node có giá trị nhỏ nhất
• Max heap: Node gốc luôn có giá trị lớn nhất

Heap cho phép trùng lặp giá trị, còn BST thì không.

Ứng dụng của Heap:

• Làm priority queue: Hàng đợi ưu tiên
• Sử dụng trong kernel Linux, để chống lưng cho thuật toán heap sort, scheduler...
• …

Map (HashMap)

Array có tốc độ truy cập phần tử O(1) khi đã biết index, nhưng index không đại diện cho giá trị của phần tử, bạn phải tìm tệ nhất là O(n) để tìm dược phần tử mong muốn.

Chúng ta có Map, hay còn gọi là Dictonary trong một vài ngôn ngữ, có thể loại bỏ được nhược điểm trên của array.

Map là một tập key-value, và key có thể là bất kỳ thứ gì bạn muốn, thay vì kiểu integer như index của Array. Đặc điểm của Map:

• Complexity: Hầu hết là O(1), còn nếu có collision cao thì O(log n) trong java ³.
• Không cho phép trùng lặp key

Làm sao để map có thể truy xuất giá trị theo key với tốc độ O(1)? Đó là do việc hashing (băm), chúng ta sẽ bàn tới trong phần tiếp theo, go!

Hashing, Collision

Khi chúng ta nói về Map, thường sẽ ám chỉ HashMap, tức là map được triển khai bằng phương pháp hashing (hàm băm).

Hashing được phát minh bởi một nhà khoa học máy tính người Đức tên là Hans Peter Luhn. Kĩ thuật này được áp dụng rất nhiều trong lập trình, từ rất bình thường như trong các cấu trúc dữ liệu tới nổi tiếng thì được sử dụng ở Blockchain.

Hashing

Hashing tức là quá trình băm dữ liệu với bất kỳ độ dài nào để có kết quả đầu ra với một độ dài đồng nhất (tùy theo thuật toán hash). Bên cạnh đó, với chung 1 dữ liệu input, chúng ta sẽ luôn luôn có output giống nhau sau khi hash.

Chúng ta có vài thuật toán hash phổ biến:

• SHA-256: Output 256 ký tự.
• MD5: Output 32 ký tự.

Vậy tại sao cần hashing? Hay nói đúng hơn là tầm quan trọng của hashing và ứng dụng của nó.

Hashing sẽ giúp quá trình tìm kiếm trở nên dễ dàng hơn vì chúng ta có một độ dài ngắn hơn so với dữ liệu gốc.

Một giải pháp thực tế là với kiểu hash index trong database. Nhìn hình sau để dễ bề hình dung ra cách hash index hoạt động:

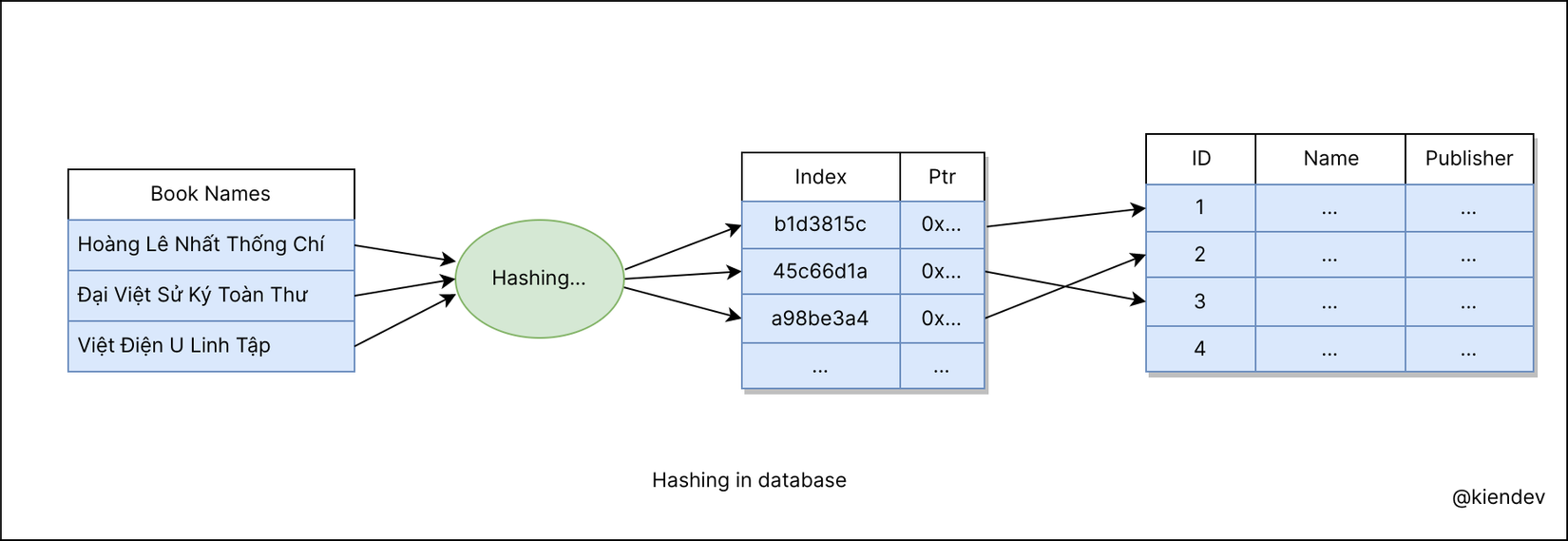
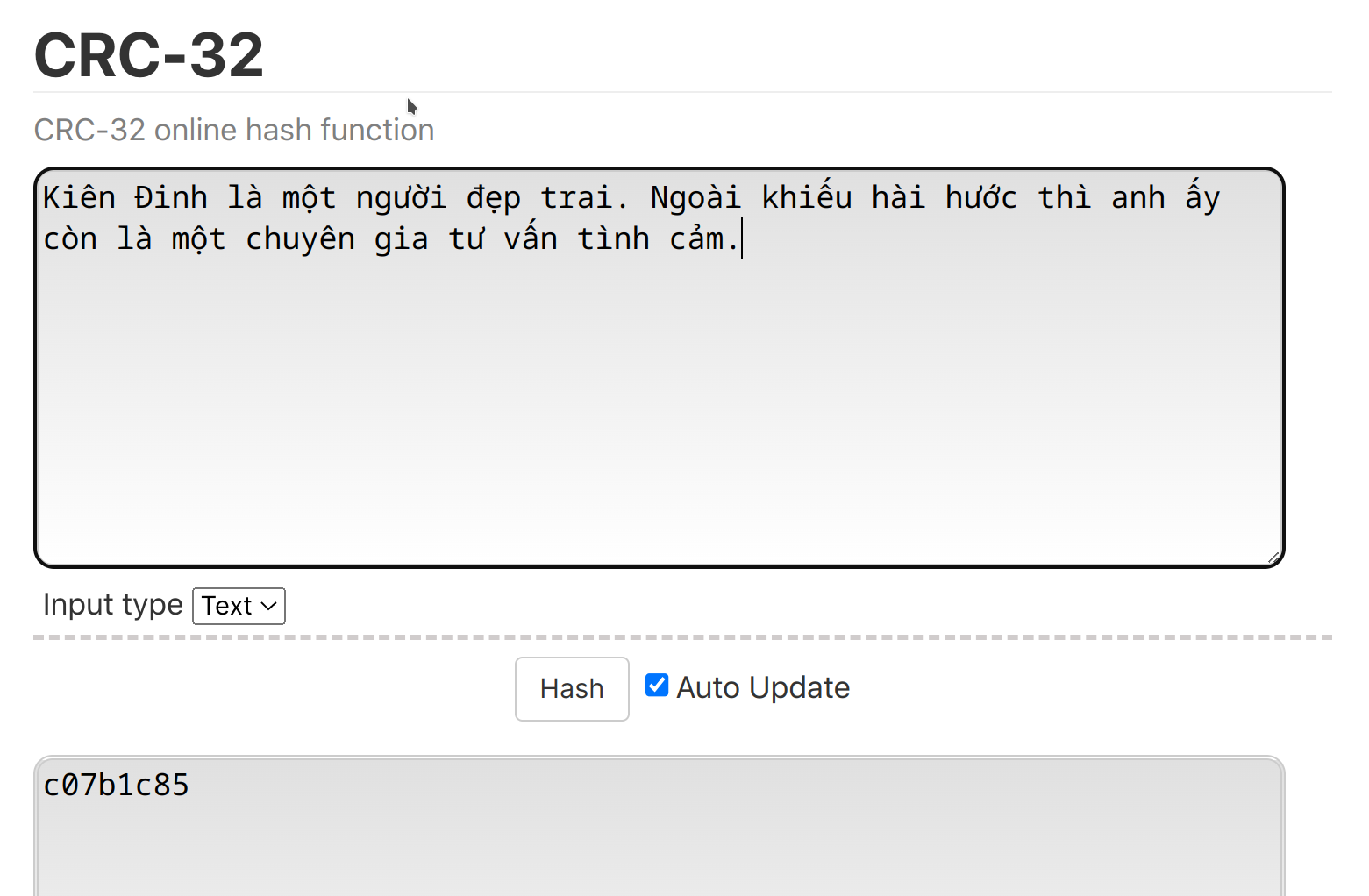
Bằng mắt ta cũng thấy được kích thước của index được lưu nhỏ hơn dữ liệu rất nhiều, đặc biệt trong trường hợp dữ liệu lưu dạng UTF-8.

Trong hình trên, Việt Điện U Linh Tập có độ dài 27 bytes, trong khi hash CRC-32 là a98be3a4 chỉ có 8 byte, tiết kiệm được rất nhiều phải không?. Trong thực tế, các database thường lưu hash bằng một giá trị integer.

---

Tại sao HashMap lại có tốc độ truy xuất nhanh: O(1)?

Bên dưới HashMap thường là một array, do đó từ kết quả hash thì có thể truy ra được index của dữ liệu trong array bên dưới bằng phép tính modulo (chia lấy dư). Tương tự, lúc chèn mới dữ liệu vào map, lúc đó index cũng sẽ được tính toán bằng cách này.

Hashing collision

Nếu như có nhiều giá trị khác nhau lại có chung một kết quả hash trùng nhau, trong khi đó một index không thể lưu 2 giá trị, khi ấy phải làm sao?

Đó là tình huống xung đột (hashing collision) xảy ra, và khi ấy ta sẽ phải áp dụng kĩ thuật khác để xử lý xung đột, trong trường hợp tệ nhất mà collision xảy ra quá nhiều, map sẽ có time complexity là O(n).

Khi có xung đột xảy ra, thì sẽ có 2 hướng để giải quyết xung đột, đó chính là Separate Chaining và Open Addressing.

Ở đây mình chỉ minh họa phương pháp separate chaining, chính là sử dụng LinkedList làm giá trị của array gốc, khi có xung đột xảy ra, cứ tìm đúng index, lấy ra linkedlist tương ứng và chèn thêm giá trị vào là xong:

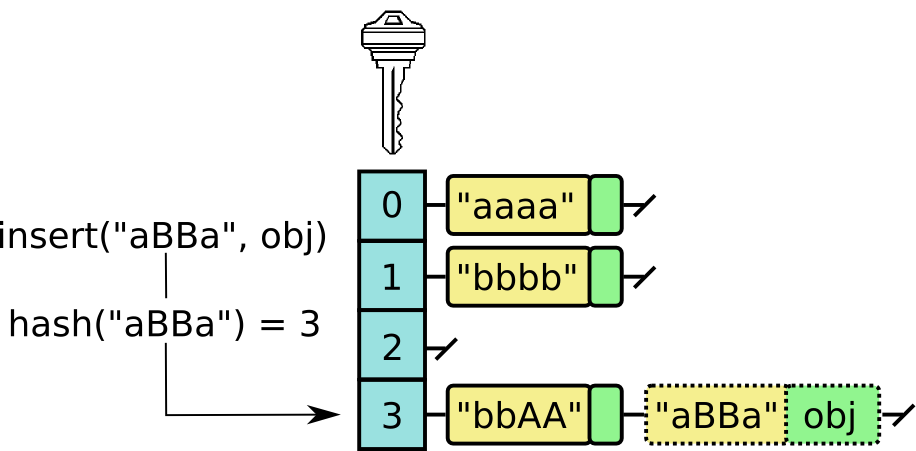
Khi implement các cấu trúc dữ liệu có sử dụng hashing và các thuật toán hash, người ta cần chú ý những điều sau cho hàm hash⁴:

• Dễ tính toán
• Phân phối đều: Giá trị trả về từ hash function sẽ giúp phân phối đều các entries trên hash table, tránh bị phân thành các cụm.
• Tránh va chạm: Tránh trường hợp bị tấn công collision attack, tức là kẻ xấu lợi dụng thuật toán hash của chương trình và đưa vào các giá trị trùng hash, dẫn tới việc tạo ra lỗ hổng bảo mật.

🍉 Lưu ý: Với các ngôn ngữ và phần mềm khác nhau, người ta có thể sử dụng một cách implement khác nhau cho HashMap. Ví dụ như từ phiên bản Java 8 trở lên thì không còn sử dụng Array và LinkedList, thay vào đó là một binary tree.

Tổng kết

Ôn lại một xíu những thuật ngữ mà chúng ta đã có trong bài viết này:

• Stack & Heap
• Call stack
• Binary Heap Tree
• Hashing
• Hashing collision
• Collision attack

Hi vọng qua bài viết này, mình có thể cung cấp cho các bạn kiến thức hữu ích về cấu trúc dữ liệu. Nếu thấy có ích, hãy ủng hộ mình bằng 1 upvote và comment phía bên dưới nhé.

Đừng quên theo dõi mình để đọc các bài viết về lập trình backend trong tương lai!

Happy coding! Happy learning!

1. https://www.linkedin.com/pulse/what-where-stack-heap-maxim-malisciuc/

2. https://www.cs.utexas.edu/users/djimenez/utsa/cs3343/lecture16.html

3. https://stackoverflow.com/questions/4553624/hashmap-get-put-complexity

4. https://icancodeit.wordpress.com/2019/08/17/hashing-va-hash-table/