Mở đầu

Hi các bạn, nay mình sẽ chia sẻ 1 chủ đề về cấu trúc dữ liệu trong android hay dùng nhé(Mình có để ví dụ cho từng loại, các bạn có thể copy code, rùi vào https://www.onlinegdb.com/online_java_compiler chạy test nhé). Trong lập trình Android, việc sử dụng cấu trúc dữ liệu và thuật toán hiệu quả là rất quan trọng để xây dựng ứng dụng di động mượt mà, nhanh chóng và hiệu quả. Cùng tìm hiểu về những cấu trúc dữ liệu và thuật toán phổ biến mà bạn có thể áp dụng trong phát triển ứng dụng Android nhé.

Các cấu trúc dữ liệu và thuật toán hay dùng

Cấu trúc dữ liệu

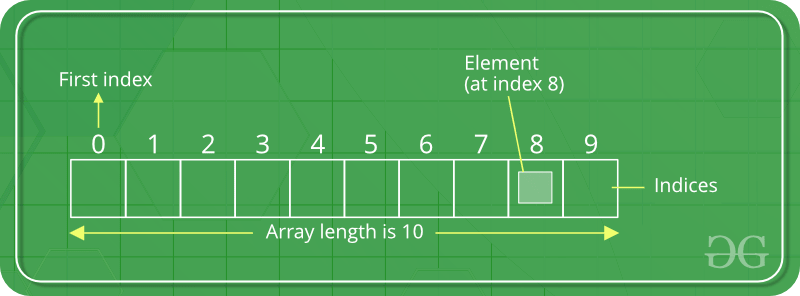
List :

• Là một tập hợp các phần tử được sắp xếp theo một thứ tự nhất định.
• Mỗi phần tử trong danh sách có một chỉ số (index) duy nhất, bắt đầu từ 0.
• Các phần tử trong danh sách có thể trùng lặp.
• Có thể truy cập, thêm, xóa hoặc sửa đổi phần tử trong danh sách thông qua chỉ số của chúng.
• Các loại List phổ biến bao gồm: Array List, Linked List, Vector, Stack, Queue, v.v.

Demo

import java.util.ArrayList;
import java.util.List;
public class Main{
public static void main(String[] args) {
List<String> myList = new ArrayList<>();

// Thêm phần tử vào danh sách
myList.add("Apple");
myList.add("Banana");
myList.add("Orange");

// In danh sách
for (String fruit : myList) {
System.out.println(fruit);
}
}
}

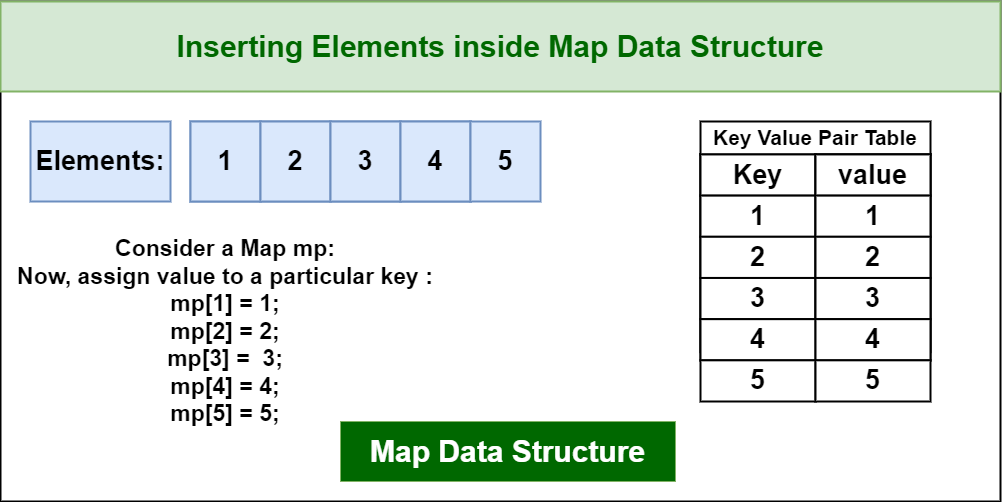
Map:

Map trong Java đại diện cho một bộ cặp key-value.

• Là một tập hợp các cặp khóa-giá trị (key-value pairs).
• Mỗi khóa trong Map là duy nhất, và được ánh xạ đến một giá trị tương ứng.
• Không có khái niệm về thứ tự trong Map, trừ khi sử dụng các loại Map đặc biệt như LinkedHashMap hoặc TreeMap.
• Có thể truy cập, thêm, xóa hoặc sửa đổi giá trị trong Map thông qua khóa tương ứng.
• Các loại Map phổ biến bao gồm: HashMap, TreeMap, LinkedHashMap, v.v.

Demo

import java.util.HashMap;
import java.util.Map;
public class Main{
public static void main(String[] args) {
Map<String, Integer> myMap = new HashMap<>();
// Thêm cặp key-value vào map
myMap.put("Alice", 25);
myMap.put("Bob", 30);
myMap.put("Charlie", 28);
// Truy cập và in ra các giá trị trong map
for (Map.Entry<String, Integer> entry : myMap.entrySet()) {
System.out.println(entry.getKey() + " is " + entry.getValue() + " years old.");
}
}
}

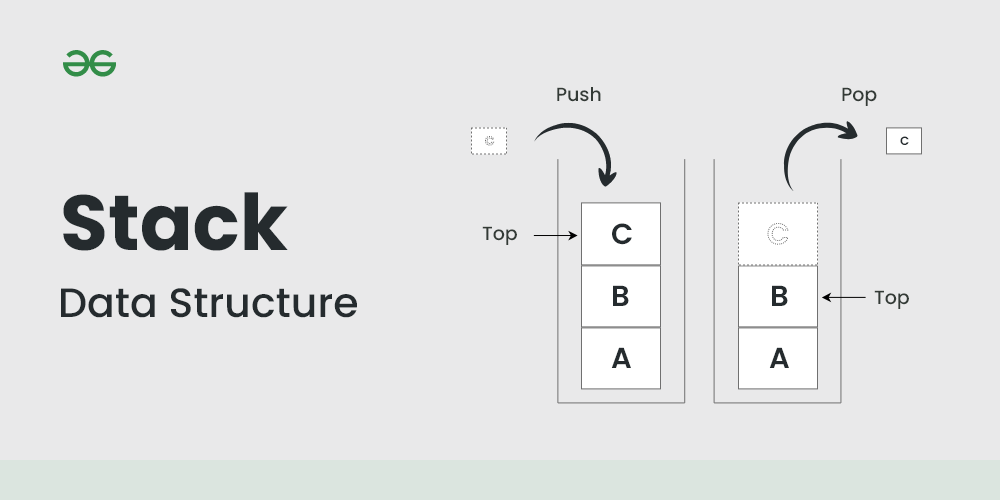
Stack:

Stack là một cấu trúc dữ liệu trừu tượng được sử dụng trong lập trình để lưu trữ và quản lý các phần tử theo cơ chế "Last In, First Out" (LIFO). Điều này có nghĩa là phần tử cuối cùng được thêm vào stack sẽ là phần tử được lấy ra đầu tiên khi thực hiện thao tác lấy ra (pop).

Demo

import java.util.Stack;
public class Main{
public static void main(String[] args) {
Stack<Integer> myStack = new Stack<>();
// Thêm phần tử vào ngăn xếp
myStack.push(10);
myStack.push(20);
myStack.push(30);
// Loại bỏ phần tử từ ngăn xếp
while (!myStack.isEmpty()) {
System.out.println(myStack.pop());
}
}
}

Thuật toán

Thuật toán sắp xếp

Có rất nhiều thuật toán sắp xếp khác nhau như quick sort, merge sort, heap sort,... trong bài này mình xin phép demo thuật toán bubble sort nhé.

Thuật toán sắp xếp Bubble Sort là một trong những thuật toán sắp xếp đơn giản nhất. Nó hoạt động bằng cách so sánh lần lượt từng cặp phần tử liền kề trong danh sách và hoán đổi chúng nếu chúng không được sắp xếp đúng thứ tự. Thuật toán này tiếp tục lặp lại quá trình này cho đến khi không còn cần phải hoán đổi nữa.

Mô tả cụ thể về thuật toán Bubble Sort:

Bắt đầu từ đầu danh sách, so sánh phần tử thứ nhất với phần tử thứ hai. Nếu phần tử thứ nhất lớn hơn phần tử thứ hai, hoán đổi chúng.

Tiếp tục so sánh phần tử thứ hai với phần tử thứ ba, và tiếp tục quá trình này cho đến khi bạn so sánh phần tử thứ lớn nhất với phần tử cuối cùng của danh sách.

Lặp lại các bước trên cho đến khi không còn có sự hoán đổi nào xảy ra trong một vòng lặp, điều này cho thấy danh sách đã được sắp xếp.

Mình xin phép ví dụ về thuật toán phổ biến ví dụ như thuật toán sắp xếp Bubble Sort:

Demo

public class Main{
public static void bubbleSort(int[] arr) {
int n = arr.length;
for (int i = 0; i < n - 1; i++) {
for (int j = 0; j < n - i - 1; j++) {
if (arr[j] > arr[j + 1]) {
// Hoán đổi các phần tử nếu cần thiết
int temp = arr[j];
arr[j] = arr[j + 1];
arr[j + 1] = temp;
}
}
}
}
public static void main(String[] args) {
int[] arr = {64, 34, 25, 12, 22, 11, 90};
bubbleSort(arr);
System.out.println("Sorted array:");
for (int num : arr) {
System.out.print(num + " ");
}
}
}

Đệ quy

Đệ quy là kỹ thuật mà một phương thức gọi chính nó. Đệ quy là một kỹ thuật trong lập trình, đặc biệt trong lập trình hàm, mà một hàm gọi lại chính nó trong quá trình thực thi. Điều này thường được sử dụng để giải quyết các bài toán được chia nhỏ thành các bài toán con giống hệt nhau hoặc tương tự nhau. Điều này giúp giảm bớt độ phức tạp của bài toán và làm cho mã nguồn trở nên rõ ràng hơn.

Kỹ thuật đệ quy thường đi kèm với một số quy tắc cần tuân theo, bao gồm điều kiện dừng để tránh vòng lặp vô hạn. Mỗi lần gọi hàm đệ quy, nó sẽ giảm kích thước của bài toán đến khi nó đạt đến trạng thái cơ bản nhất và có thể giải quyết trực tiếp mà không cần gọi lại hàm nữa.

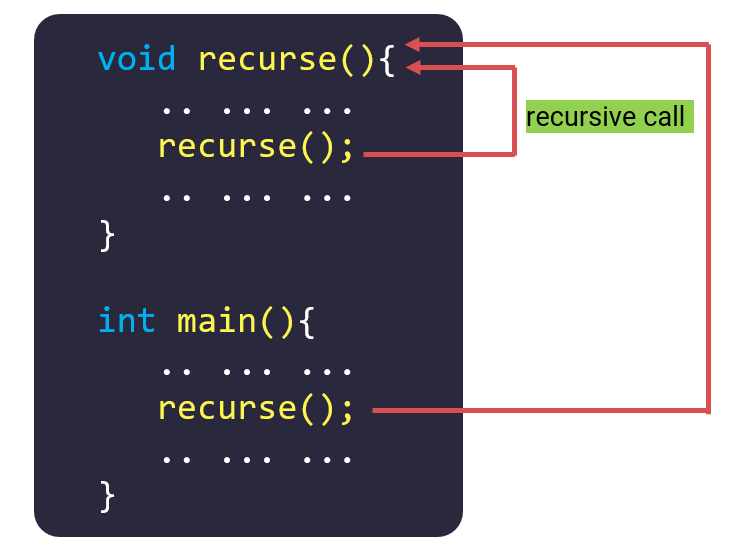
Dưới đây là một ví dụ về đệ quy trong việc tính giai thừa:

Demo

public class Main{
public static int factorial(int n) {
if (n == 0 || n == 1) {
return 1;
} else {
return n * factorial(n - 1);
}
}
public static void main(String[] args) {
int number = 5;
int result = factorial(number);
System.out.println("Factorial of " + number + " is: " + result);
}
}

Tìm kiếm

Thuật toán tìm kiếm phổ biến nhất là tìm kiếm nhị phân (binary search). Thuật toán này được sử dụng để tìm kiếm một phần tử cụ thể trong một mảng đã được sắp xếp theo thứ tự tăng dần hoặc giảm dần. Cách hoạt động của thuật toán là so sánh phần tử ở giữa với giá trị cần tìm. Nếu phần tử này bằng giá trị cần tìm, ta đã tìm thấy nó. Nếu không, ta xác định xem phần tử cần tìm có lớn hơn hay nhỏ hơn phần tử ở giữa, và tiếp tục tìm kiếm trong nửa mảng thích hợp. Thuật toán này được gọi là "nhị phân" bởi vì mỗi lần tìm kiếm, ta chỉ cần xem xét một nửa của dãy số còn lại. Điều này giúp giảm đáng kể số lần so sánh cần thiết so với tìm kiếm tuyến tính, đặc biệt là đối với các mảng lớn.

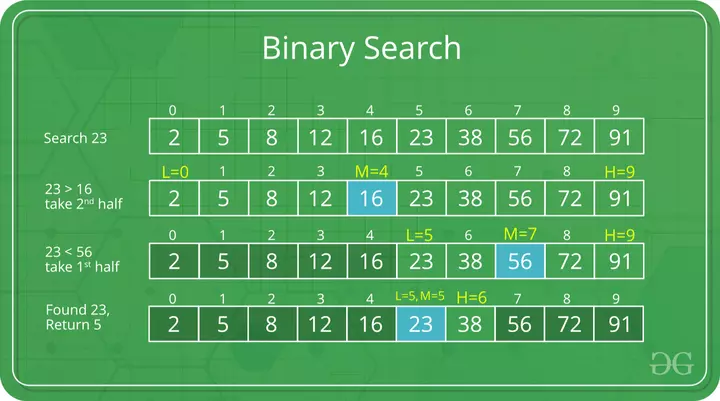
Demo

public class Main{
public static int binarySearch(int[] arr, int target) {
int left = 0;
int right = arr.length - 1;
while (left <= right) {
int mid = left + (right - left) / 2;
if (arr[mid] == target) {
return mid;
}
if (arr[mid] < target) {
left = mid + 1;
} else {
right = mid - 1;
}
}
return -1; // Trả về -1 nếu không tìm thấy
}
public static void main(String[] args) {
int[] arr = {2, 3, 4, 10, 40};
int target = 10;
int result = binarySearch(arr, target);
if (result == -1) {
System.out.println("Element not present in array");
} else {
System.out.println("Element found at index " + result);
}
}
}

Chia để trị

Thuật toán "Chia để Trị" (Divide and Conquer) là một kỹ thuật giải quyết vấn đề bằng cách chia vấn đề lớn thành các vấn đề nhỏ hơn, giải quyết các vấn đề nhỏ đó và sau đó kết hợp các lời giải của chúng để tạo ra lời giải cho vấn đề ban đầu. Kỹ thuật này thường được sử dụng để giải quyết các bài toán có tính đệ quy cao và có thể chia nhỏ thành các bài toán con tương tự.

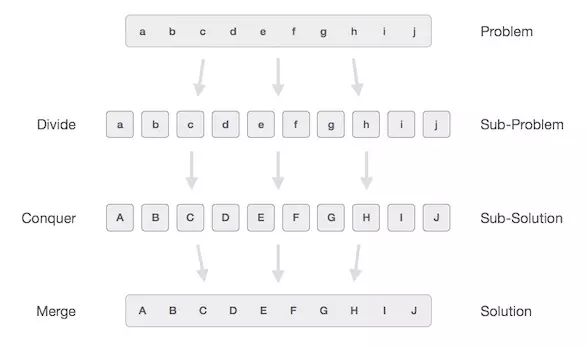
Demo

public class MergeSort {

    // Hàm trộn hai mảng đã được sắp xếp thành một mảng mới
    public static void merge(int[] arr, int left, int middle, int right) {
        // Tìm kích thước của hai mảng con để merge
        int n1 = middle - left + 1;
        int n2 = right - middle;

        // Tạo các mảng tạm
        int[] leftArr = new int[n1];
        int[] rightArr = new int[n2];

        // Sao chép dữ liệu vào các mảng tạm
        for (int i = 0; i < n1; ++i)
            leftArr[i] = arr[left + i];
        for (int j = 0; j < n2; ++j)
            rightArr[j] = arr[middle + 1 + j];

        // Trộn hai mảng tạm vào arr
        int i = 0, j = 0; // Chỉ số khởi tạo
        int k = left; // Chỉ số khởi tạo của mảng hợp nhất

        while (i < n1 && j < n2) {
            if (leftArr[i] <= rightArr[j]) {
                arr[k] = leftArr[i];
                i++;
            } else {
                arr[k] = rightArr[j];
                j++;
            }
            k++;
        }

        // Sao chép các phần tử còn lại của mảng, nếu có
        while (i < n1) {
            arr[k] = leftArr[i];
            i++;
            k++;
        }

        while (j < n2) {
            arr[k] = rightArr[j];
            j++;
            k++;
        }
    }

    // Hàm sắp xếp mảng bằng thuật toán chia để trị
    public static void sort(int[] arr, int left, int right) {
        if (left < right) {
            // Tìm điểm chính giữa để chia mảng thành hai nửa
            int middle = left + (right - left) / 2;

            // Chia hai nửa và gọi đệ quy để sắp xếp chúng
            sort(arr, left, middle);
            sort(arr, middle + 1, right);

            // Trộn hai nửa đã được sắp xếp
            merge(arr, left, middle, right);
        }
    }

    public static void main(String[] args) {
        int[] arr = { 12, 11, 13, 5, 6, 7 };

        System.out.println("Mảng ban đầu: ");
        printArray(arr);

        sort(arr, 0, arr.length - 1);

        System.out.println("\nMảng sau khi sắp xếp: ");
        printArray(arr);
    }

    // Hàm in mảng
    static void printArray(int[] arr) {
        for (int val : arr)
            System.out.print(val + " ");
        System.out.println();
    }
}

Kết

KHI HỌC BẤT CỨ KIẾN THỨC NÀO, HÃY CHỦ ĐỘNG TÌM HIỂU THẬT KĨ VÀ HIỂU BẢN CHẤT!

Tài liệu:

VNOI: https://vnoi.info/wiki/gollum/overview/algo/

Data Structures: https://www.youtube.com/playlist?list=PL6Zs6LgrJj3tDXv8a_elC6eT_4R5gfX4d

Ông Dev: https://www.youtube.com/watch?v=Q7UuJAhysZg&list=PLoaAbmGPgTSNMAzkKBHkh2mLuBk54II5L

Thuật toán ứng dụng: https://daotao.ai/courses/thuat-toan-ung-dung/

Git Thuật toán Java: https://github.com/TheAlgorithms/Java/blob/master/DIRECTORY.md

GpCoder: https://gpcoder.com/