3.7K 111 50

Đã đăng vào thg 12 17, 2019 12:59 SA 12 phút đọc

141.9K

Các thuật toán sắp xếp cơ bản

Bài đăng này đã không được cập nhật trong 3 năm

Cuộc sống luôn chứa đựng quá nhiều vấn đề khiến chúng ta mệt mỏi. Dẹp hết đi hoặc sắp xếp lại mọi thứ, biết đâu bạn sẽ cảm thấy ổn hơn

Chủ đề "thuật toán sắp xếp" đã nảy ra trong đầu mình theo dòng suy nghĩ ấy. Tuy rằng không phải sở trường nhưng mình sẽ cố gắng để bài viết này có ích Cùng mình tìm hiểu nhé!

1. Ừ là Khái niệm

Bài toán sắp xếp là bài toán giải quyết việc tổ chức dữ liệu theo một trật tự nhất định, thường là tăng dần hoặc giảm dần.

Tóm tắt bài toán sắp xếp tăng dần:

Input: Một mảng n phần tử A = ( $a_1, a_2, a_3, ..., a_n$ )

Output: Một hoán vị của A là mảng A' = ( $a'_1, a'_2, a'_3, ..., a'_n$ ), thỏa mãn điều kiện: $a'_1 <= a'_2 <= a'_3 <= ... <= a'_n$

2 phép toán cơ bản cho bài toán sắp xếp:

1. Phép toán đổi chỗ: Là phép toán đảo giá trị 2 biến

void swap(datatype &a, datatype &b) {
datatype temp = a; //datatype-kiểu dữ liệu của phần tử
    a = b;
    b = temp;
}

2. Phép toán so sánh: Trả về true nếu a > b và trả về false cho trường hợp ngược lại.

compare(datatype a, datatype b) {
    if (a > b) {
        return true;
    } else {
        return false;
    }
}

Đây là 2 phép toán con thường được sử dụng trong các bài toán sắp xếp. Giống như phép +- trong số học vậy.

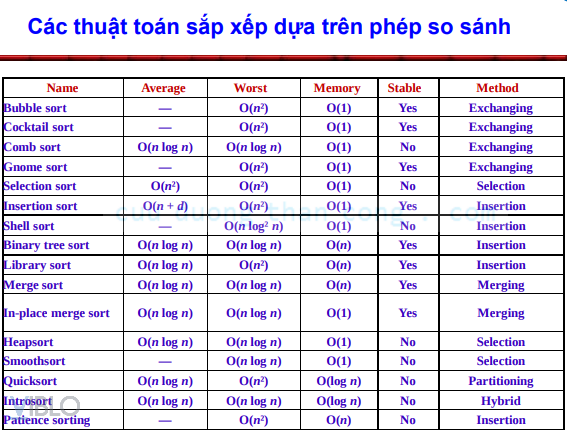
2. Ba thuật toán sắp xếp cơ bản

2.1. Sắp xếp chèn (Insertion Sort)

Ý tưởng: Insertion Sort lấy ý tưởng từ việc chơi bài, dựa theo cách người chơi "chèn" thêm một quân bài mới vào bộ bài đã được sắp xếp trên tay.

Thuật toán:

Tại bước k = 1, 2, ..., n đưa phần tử thứ k trong mảng đã cho vào đúng vị trí trong dãy gồm k phần tử đầu tiên.
Kết quả là sau bước thứ k, sẽ có k phần tử đầu tiên được sắp xếp theo thứ tự.

void insertionSort(int a[], int array_size) {
    int i, j, last;
    for (i=1; i < array_size; i++) {
        last = a[i];
        j = i;
    while ((j > 0) && (a[j-1] > last)) {
        a[j] = a[j-1];
        j = j - 1; }
        a[j] = last;
    } // end for
} // end of isort

Ví dụ:

Đánh giá:

Best Case: 0 hoán đổi, n-1 so sánh (khi dãy đầu vào là đã được sắp)
Worst Case: $n^2$ /2 hoán đổi và so sánh (khi dãy đầu vào có thứ tự ngược lại với thứ tự cần sắp xếp)
Average Case: $n^2$ /4 hoán đổi và so sánh

2.2. Sắp xếp lựa chọn (Selection Sort)

Ý tưởng của Selection sort là tìm từng phần tử cho mỗi vị trí của mảng hoán vị A' cần tìm.

Thuật toán:

Tìm phần tử nhỏ nhất đưa vào vị trí 1
Tìm phần tử nhỏ tiếp theo đưa vào vị trí 2
Tìm phần tử nhỏ tiếp theo đưa vào vị trí 3
...

void selectionSort(int a[], int n){
    int i, j, min, temp;
    for (i = 0; i < n-1; i++) {
        min = i;
        for (j = i+1; j < n; j++){
            if (a[j] < a[min]) min = j;
        }
        swap(a[i], a[min]);
    }
}

Ví dụ:

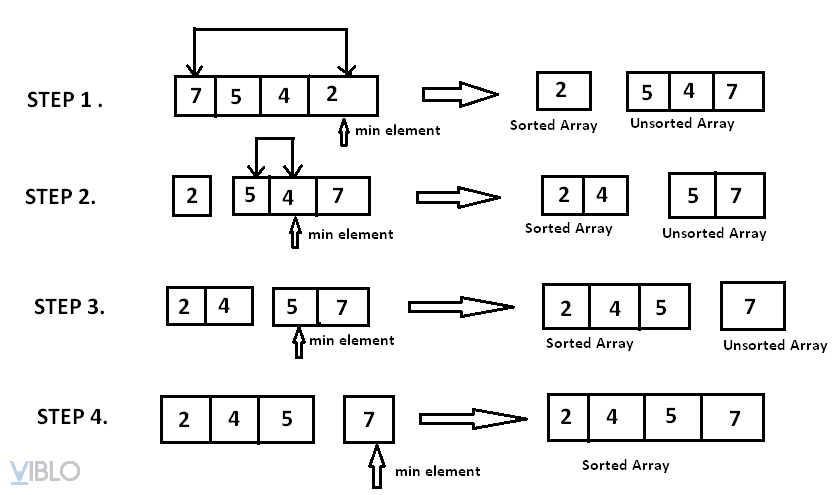
Đánh giá:

Best case: 0 đổi chỗ (n-1 như trong đoạn mã), $n_2$ /2 so sánh.
Worst case: n - 1 đổi chỗ và $n^2$ /2 so sánh.
Average case: O(n) đổi chỗ và $n^2$ /2 so sánh.

2.3. Sắp xếp nổi bọt (Bubble Sort)

Ý tưởng: Bubble Sort, như cái tên của nó, là thuật toán đẩy phần tử lớn nhất xuống cuối dãy, đồng thời những phần tử có giá trị nhỏ hơn sẽ dịch chuyển dần về đầu dãy. Tựa như sự nổi bọt vậy, những phần tử nhẹ hơn sẽ nổi lên trên và ngược lại, những phần tử lớn hơn sẽ chìm xuống dưới.

Thuật toán: Duyệt mảng từ phần tử đầu tiên. Ta sẽ so sánh mỗi phần tử với phần tử liền trước nó, nếu chúng đứng sai vị trí, ta sẽ đổi chỗ chúng cho nhau. Quá trình này sẽ được dừng nếu gặp lần duyệt từ đầu dãy đến cuối dãy mà không phải thực hiện đổi chỗ bất kì 2 phần từ nào (tức là tất cả các phần tử đã được sắp xếp đúng vị trí).

void bubbleSort(int a[], int n){
    int i, j;
    for (i = (n-1); i >= 0; i--) {
        for (j = 1; j <= i; j++){
            if (a[j-1] > a[j])
            swap(a[j-1],a[j]);
        }
    }
}

Ví dụ: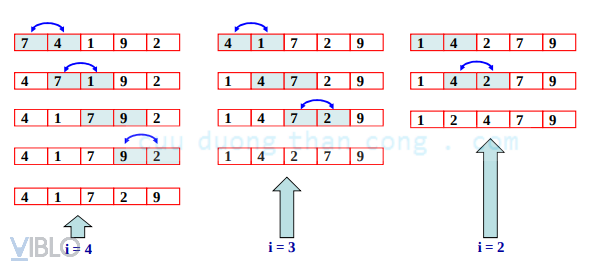

Đánh giá: Tuy đơn giản nhưng Bubble là thuật toán kém hiệu quả nhất trong 3 thuật toán ở mục này

Best case: 0 đổi chỗ, $n^2$ /2 so sánh.
Worst case: $n^2$ /2 đổi chỗ và so sánh.
Average case: $n^2$ /4 đổi chỗ và $n^2$ /2 so sánh.

So sánh 3 thuật toán

3. Merge Sort

Sắp xếp trộn (merge sort) là một thuật toán sắp xếp loại so sánh. Thuật toán này là một ví dụ tương đối điển hình của lối thuật toán chia để trị của John von Neumann:

Chia (Divide): Chia dãy gồm n phần tử cần sắp xếp thành 2 dãy, mỗi dãy có n/2 phần tử.
Trị (Conquer): Sắp xếp mỗi dãy con một cách đệ quy sử dụng sắp xếp trộn. Khi dãy chỉ còn một phần tử thì trả lại phần tử này.
Tổ hợp (Combine): Trộn (Merge) hai dãy con được sắp xếp để thu được dãy được sắp xếp gồm tất cả các phần tử của cả hai dãy con.

Thuật toán:

MERGE-SORT(A, p, r)
    if p < r 
        then q ← (p + r)/2 // Chia (Divide)
            MERGE-SORT(A, p, q) // Trị (Conquer)
            MERGE-SORT(A, q + 1, r) // Trị (Conquer)
            MERGE(A, p, q, r) // Tổ hợp (Combine)
    endif

Thuật toán trộn:

Giả sử có hai dãy đã được sắp xếp L[1.. $n_1$ ] và R[1.. $n_2$ ]. Ta có thể trộn chúng lại thành một dãy mới M[1.. $n_1 + n_2$ ] được sắp xếp theo cách sau:

So sánh hai phần tử đứng đầu của hai dãy, lấy phần tử nhỏ hơn cho vào dãy mới. Tiếp tục như vậy cho tới khi một trong hai dãy rỗng.
Khi một trong hai dãy rỗng, ta lấy phần còn lại của dãy kia cho vào cuối dãy mới.

Khi đó, ta sẽ thu được dãy cần tìm.

MERGE(M, p, q, r)
    // Sao n1 phần tử đầu tiên vào L[1 . . n1] và n2 phần tử tiếp theo vào R[1 . . n2]
    // L[n1 + 1] ← infty; R[n2 + 1] ← infty
    i ← 1; j ← 1
    for k ← p to r do
        if L[ i ] ≤ R[ j ]
        then
            M[k] ← L[ i ]
            i ←i + 1
        else
            M[k] ← R[ j ]
            j ← j + 1

Đánh giá: O(n*logn)

Ví dụ:

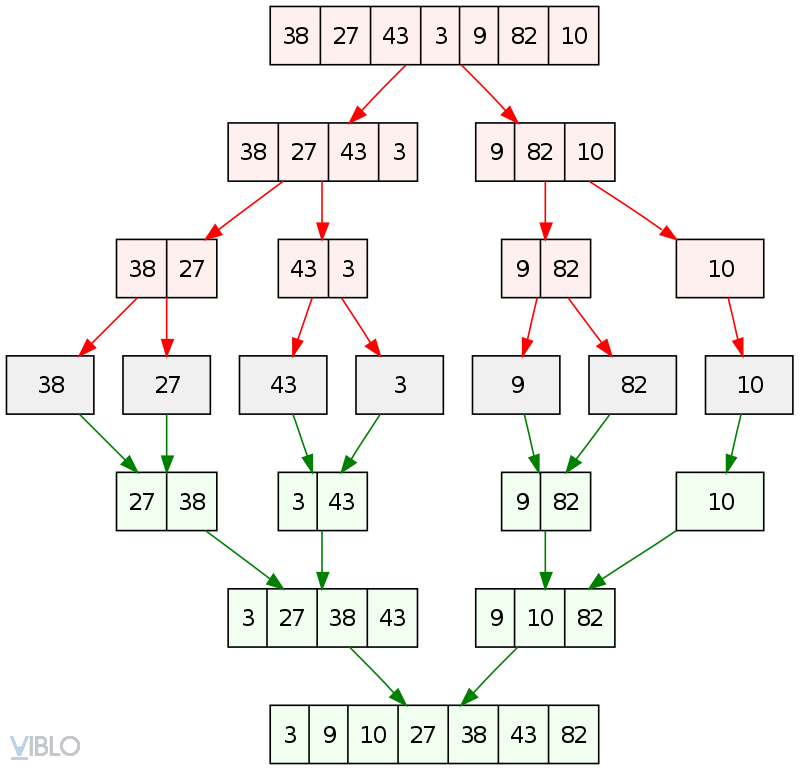
4. Quick Sort

Quick Sort (QS) được phát triển bởi Hoare năm 1960. Theo thống kê tính toán, QS là thuật toán sắp xếp nhanh nhất hiện nay.

QS có thời gian tính trung bình là O(n*log n), tuy nhiên thời gian tính tồi nhất của nó lại là O( $n_2$ ).

Tương tự như Merge sort, Quick sort là thuật toán sắp xếp được phát triển dựa trên kỹ thuật chia để trị:

Neo đệ qui (Base case). Nếu dãy chỉ còn một phần tử thì nó là dãy đã sắp xếp và trả lại dãy này mà không phải làm gì cả.
Chia (Divide):
- Chọn một phần tử trong dãy và gọi nó là phần tử chốt p (pivot).
- Chia dãy đã cho ra thành hai dãy con: Dãy con trái (L) gồm những phần tử không lớn hơn phần tử chốt, còn dãy con phải (R) gồm các phần tử không nhỏ hơn phần tử chốt. Thao tác này được gọi là thao tác Phân đoạn (Partition).
Trị (Conquer): Lặp lại một cách đệ qui thuật toán đối với hai dãy con L và R.
Tổng hợp (Combine): Dãy được sắp xếp là L p R.

Thuật toán:

Quick-Sort(A, Left, Right)
    if (Left < Right ) {
        Pivot = Partition(A, Left, Right);
        Quick-Sort(A, Left, Pivot – 1);
        Quick-Sort(A, Pivot + 1, Right); }

Chọn phần tử chốt:

Việc chọn phần tử chốt nắm vai trò quyết định đối với hiệu năng của thuật toán. Tốt nhất là chọn phần tử chốt là trung vị của danh sách. Tuy nhiên cách này rất khó nên ta có thể chọn phần tử chốt theo những cách sau:

Chọn phần tử đứng đầu hoặc đứng cuối làm phần tử chốt.
Chọn phần tử đứng giữa dãy làm phần tử chốt.
Chọn phần tử trung vị trong 3 phần tử đứng đầu, đứng giữa và đứng cuối làm phần tử chốt.
Chọn phần tử ngẫu nhiên làm phần tử chốt. (Cách này có thể dẫn đến khả năng rơi vào các trường hợp đặc biệt).

Thuật toán Phân đoạn Partition: Mục đích của hàm Partition(A, left, right) là chia A[left..right] thành hai đoạn A[left..pivot –1] và *A[pivot+1..right], sao cho:

A[left..pivot –1] là tập hợp các phần tử có giá trị nhỏ hơn hoặc bằng A[pivot].
A[pivot+1..right] là tập hợp các phần tử có gía trị lớn hơn A[pivot].

Ví dụ của QS:

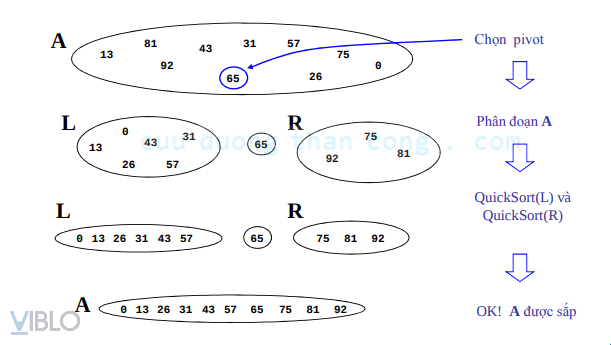
Đánh giá: Thời gian tính của Quick-Sort phụ thuộc vào việc phép phân đoạn là cân bằng (balanced) hay không cân bằng (unbalanced), và điều này lại phụ thuộc vào việc chọn phần tử chốt.

Phân đoạn không cân bằng: O( $n_2$ )
Phân đoạn hoàn hảo: O(n*logn)

5. Heap Sort

Định nghĩa

Heap (đống) là cây nhị phân gần hoàn chỉnh có hai tính chất:

Tính cấu trúc (Structural property): tất cả các mức đều đầy đủ node con, ngoại trừ mức cuối cùng. Mức cuối được điền từ trái sang phải.
Tính có thứ tự hay tính chất đống (heap property): với mỗi nút x, có Parent(x) ≥ x.

Biểu diễn đống dưới dạng mảng, ta có:

Gốc của cây là A[1]
Con trái của A[i] là A[2i]*
Con phải của A[i] là A[2i + 1]*
Cha của A[i] là A[ i/2 ]
Số lượng phần tử của heap là Heapsize[A] ≤ length[A]

Phân loại: Có 2 loại

Max-heaps (Phần tử lớn nhất ở gốc): với mọi nút i, ngoại trừ gốc: A[parent(i)] ≥ A[i]
Min-heaps (Phần tử nhỏ nhất ở gốc): với mọi nút i, ngoại trừ gốc: A[parent(i)] ≤ A[i]

Chúng ta sẽ xét bài toán với max-heap, min-heap tương tự.

Phép toán khôi phục tính chất max-heap (Vun lại đống)

Xét bài toán:

Giả sử có nút i với giá trị bé hơn con của nó và cây con trái và cây con phải của i đều là max-heaps

Thuật toán đệ quy:

Đổi chỗ i với con lớn hơn
Di chuyển xuống theo cây
Tiếp tục quá trình cho đến khi node i không còn bé hơn con.

Max-Heapify(A, i, n)
    // n = heapsize[A]
    l ← left-child(i); r ← right-child(i);
    if (l ≤ n) and (A[l] > A[i])
        then largest ← l
        else largest ← i
    if (r ≤ n) and (A[r] > A[largest])
        then largest ← r
    if largest != i
        then Exchange(A[i],A[largest])
    Max-Heapify(A,largest,n)

Ví dụ:

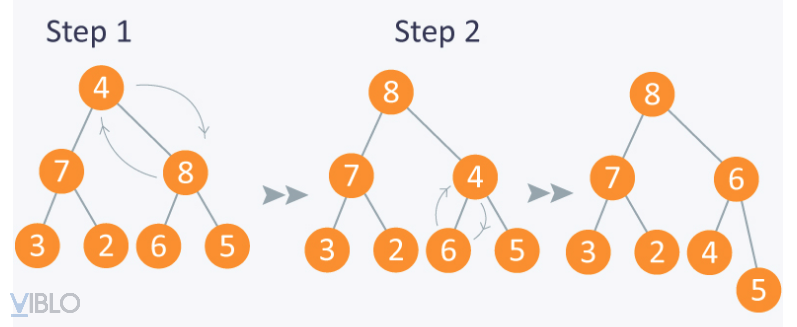
Thuật toán Heapsort

Ý tưởng: Với A là một max-heap, nếu mỗi cây con có node cha từ 1 đến n/2 đều là max-heaps thì A là một mảng sắp xếp giảm dần.

Build-Max-Heap(A)
    n = length[A]
    for i ← n/2 downto 1
        do Max-Heappify(A, i, n)

Ví dụ:

Trên đây là một số những thuật toán sắp xếp mình đã tìm hiểu, nếu có gì sai sót, bạn góp ý cho mình nhé.

Hi vọng bài viết này có ích với bạn. Hẹn gặp lại bạn ở những bài viết tiếp theo.

Tài liệu tham khảo:

Cấu trúc dữ liệu và thuật toán - Nguyễn Đức Nghĩa, nhà xuất bản Bách Khoa Hà Nội, 2013

Mergesort

Quicksort

Heap sort

1. Ừ là Khái niệm

2. Ba thuật toán sắp xếp cơ bản

2.1. Sắp xếp chèn (Insertion Sort)

2.2. Sắp xếp lựa chọn (Selection Sort)

2.3. Sắp xếp nổi bọt (Bubble Sort)

3. Merge Sort

4. Quick Sort

5. Heap Sort

Mục lục