Build ứng dụng Augmented Reality đơn giản với OpenCV [Phần 1]

Mở đầu

Vừa rồi mình có tìm hiểu qua về cách map 3D object trong Augmented Reality (AR), nhân tiện chia sẻ với các bạn. Về AR - Công nghệ cho phép con người quan sát thế giới thực trực tiếp hoặc gián tiếp thông qua các thiết bị, các thành phần của môi trường sẽ được bổ sung thêm tạo trải nghiệm mới cho người quan sát. Các thành phần bổ sung đó có thể là hình ảnh, âm thanh, gia tốc ... Một vài ứng dụng nổi tiếng như Pokemon Go, AR Card, AR Watches ...

Demo Simple AR:

Tổng quan

Để map 3D object với hình ảnh thế giới thực thì cần có các thông tin về vị trí, tỉ lệ và hướng. Để thực hiện điều này, chúng ta chọn 1 vật thể trong thế giới thực để tham chiếu. Thiết bị AR thu lại hình ảnh thực, sau đó nhận diện vật tham chiếu bao gồm vị trí, sự thay đổi đặc điểm qua các frame ảnh. Để tính toán sự thay đổi của vật tham chiếu, chúng ta có thể dùng phép biến đổi homography. Nhưng như vậy vẫn chưa đủ để map 3D object lên hình ảnh thế giới thực vì khi vật tham chiếu thay đổi trạng thái, chúng ta cũng muốn quan sát 3D object thay đổi về góc độ, tỉ lệ .. tương ứng. Do vậy cần thêm 1 hệ toạ độ khác dành riêng cho việc quan sát 3D object. Mỗi khi vật tham chiếu thay đổi trạng thái, việc quan sát 3D object cũng được tính toán lại rồi đưa hình ảnh lên màn.

Túm váy lại, chúng ta có pipeline như sau:

1. Nhận diện vật tham chiếu -> 2. Ước lượng biến đổi đồng nhất -> 3. Tính toán hệ quan sát 3D object -> 4. Draw hình ảnh 3D object lên hình ảnh thế giới thực.

Để tiện thực hành, mình lấy thẻ card làm vật tham chiếu (chọn bề mặt phẳng vì nó dễ): Lưu ý không chọn thẻ đơn sắc nhé các bạn =))

Nhận diện vật tham chiếu

Ở bước này, mình sử dụng opencv để detect các keypoint trên ảnh gốc của vật tham chiếu và các ảnh cần nhận diện vật tham chiếu. Sau đó sử dụng feature matching để nhận diện vật tham chiếu trên ảnh mới. Kết quả là: Việc detect keypoint, các bạn có thể sử dụng các thuật toán như ORB, SIFT, SURT

Code sample:

import cv2

cap = cv2.imread('sample1.jpg', 0)    
model = cv2.imread('refer.jpg', 0)
orb = cv2.ORB_create()
bf = cv2.BFMatcher(cv2.NORM_HAMMING, crossCheck=True)
kp_model, des_model = orb.detectAndCompute(model, None)
kp_frame, des_frame = orb.detectAndCompute(cap, None)
matches = bf.match(des_model, des_frame)
matches = sorted(matches, key=lambda x: x.distance)

cap = cv2.drawMatches(model, kp_model, cap, kp_frame, matches, 0, flags=2)
cv2.imshow('frame', cap)
cv2.waitKey(0)

Homography estimation

Các bạn xem thêm bài viết rất hay của tác giả Nguyễn Thành Trung tại đây nhé. Mình xin nhắc lại một chút:

Khi cần ước lượng 1 vị trí x', y' mới tương ứng vị trí x, y cũ trên bề mặt tham chiếu:

$$\begin{bmatrix} x'. k \\ y'.k \\ k \end{bmatrix}=H\begin{bmatrix} \ x \\ y \\1\end{bmatrix}$$

Bước này giúp chúng ta có được ma trận H rất quan trọng cho việc tính toán ở bước sau

Sample code:

src_pts = np.float32([kp_model[m.queryIdx].pt for m in matches]).reshape(-1, 1, 2)
dst_pts = np.float32([kp_frame[m.trainIdx].pt for m in matches]).reshape(-1, 1, 2)
H, mask = cv2.findHomography(src_pts, dst_pts, cv2.RANSAC, 5.0)

Tính toán cho hệ quan sát 3D object

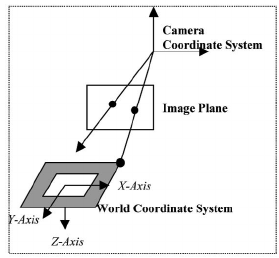
Cũng giống như việc ghi hình ảnh trong thế giới thực, việc ghi lại hình ảnh của 3D object cũng cần có 1 camera ảo để ghi hình:

$$\begin{bmatrix} u . k \\ v.k \\ k \end{bmatrix}=\begin{bmatrix} \ f_u & 0&u_0 \\ 0&f_v&v_0 \\ 0&0&1 \end{bmatrix}\begin{bmatrix} x^{cam} \\ y^{cam} \\ z^{cam} \end{bmatrix}$$

Trong đó:

• u, v là tọa độ điểm ảnh
• k là hệ số tỉ lệ
• $f_u$, $f_v$ là tiêu cự ống kính
• $x^{cam}$, $y^{cam}$ , $z^{cam}$ là tọa độ tại 1 điểm p của camera trong hệ tọa độ quan sát 3D object

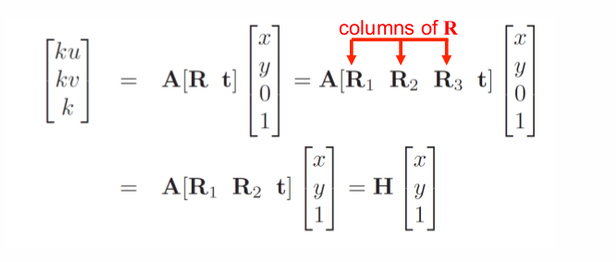
Công thức trên giúp ta thu được hình ảnh của 3D object tại 1 vị trí p của camera trong hệ quan sát. Để lấy ánh xạ sang hình ảnh thế giới thực cần thêm bước tính toán:

$$\begin{bmatrix} u . k \\ v.k \\ k \end{bmatrix}=\begin{bmatrix} \ f_u & 0&u_0 \\ 0&f_v&v_0 \\ 0&0&1 \end{bmatrix}\begin{bmatrix} \ r_{11} & r_{12}&r_{13}&t_x \\r_{11} & r_{12}&r_{13}&t_y \\ r_{11} & r_{12}&r_{13}&t_z \end{bmatrix}\begin{bmatrix} x \\ y \\ z \\1\end{bmatrix}$$

Trong đó:

• x, y, z là tọa độ vật thể trong hệ tọa độ quan sát 3D object
• Ma trận mới thêm vào là ma trận đồng nhất (tạm gọi là ma trận G) giúp chuyển hóa từ 3D -> 2D. chúng ta cần tìm ma trận này.

Thật may khi xét trong trường hợp đặc biệt, tất cả các điểm cần ánh xạ nằm trên mặt phẳng tham chiếu, lúc này z = 0 nên ta có thể rút gọn công thức trên thành:

Trong đó:

• H là ma trận đồng nhất mà ta tìm được ở bước Homography estimation

Cho $f_v$ và $f_u$ là số do cấu hình của camera, như vậy ma trận A xác định. Từ các dữ liệu trên chúng ta tính ra được $R_1$, $R_2$ và t
$R_3$ được tính theo công thức: $R_1$ x $R_2$
Túm lại phát nữa là ta đã tìm được ma trận giúp chuyển hóa từ 3D -> 2D. Tuy nhiên, quá trình tính toán phụ thuộc vào một số tham số như $f_v$ và $f_u$ nên chọn khá vất vả. Và có kinh nghiệm khác để tìm ma trận G đỡ vất hơn, mình sẽ chia sẻ chi tiết sau.

Sample code:

def projection_matrix(camera_parameters, homography):
    homography = homography * (-1)
    rot_and_transl = np.dot(np.linalg.inv(camera_parameters), homography)
    col_1 = rot_and_transl[:, 0]
    col_2 = rot_and_transl[:, 1]
    col_3 = rot_and_transl[:, 2]
    # normalise vectors
    l = math.sqrt(np.linalg.norm(col_1, 2) * np.linalg.norm(col_2, 2))
    rot_1 = col_1 / l
    rot_2 = col_2 / l
    translation = col_3 / l
    # compute the orthonormal basis
    c = rot_1 + rot_2
    p = np.cross(rot_1, rot_2)
    d = np.cross(c, p)
    rot_1 = np.dot(c / np.linalg.norm(c, 2) + d / np.linalg.norm(d, 2), 1 / math.sqrt(2))
    rot_2 = np.dot(c / np.linalg.norm(c, 2) - d / np.linalg.norm(d, 2), 1 / math.sqrt(2))
    rot_3 = np.cross(rot_1, rot_2)
    # finally, compute the 3D projection matrix from the model to the current frame
    projection = np.stack((rot_1, rot_2, rot_3, translation)).T
    return np.dot(camera_parameters, projection)

Trong đó:

• camera_parameters là ma trận A
• homography là ma trận H

Hàm sử dụng A và H để tính toán ra $R_3$ (rot_3), cuối cùng hàm trả về tích của A và G

Phần code cho render mình sẽ trình bày ở phần sau.

Tài liệu tham khảo

• https://www.mdeditor.tw/pl/2WTa
• https://www.pyimagesearch.com/2021/01/04/opencv-augmented-reality-ar/