Nguyễn Tiến Đạt @nguyen.tien.datb

1.3K 91 17

Đã đăng vào thg 9 7, 2019 6:33 SA 13 phút đọc

1.2K

Basic of Neural Network programing

Bài đăng này đã không được cập nhật trong 4 năm

Xin chào các bạn tiếp tục bài viết thứ 2 của series, nếu chưa đọc bài viết 1 bạn có đọc tại đây. Nào ta cùng bắt đầu.

Mục tiêu của bài viết này:

Xây dựng mô hình hồi quy logistic được cấu trúc như một mạng lưới thần kinh
Thực hiện các bước chính của thuật toán ML
Hiểu cách tính đạo hàm cho hồi quy logistic, sử dụng backpropagation

Notation

Các ký hiệu dùng trong bài viết:

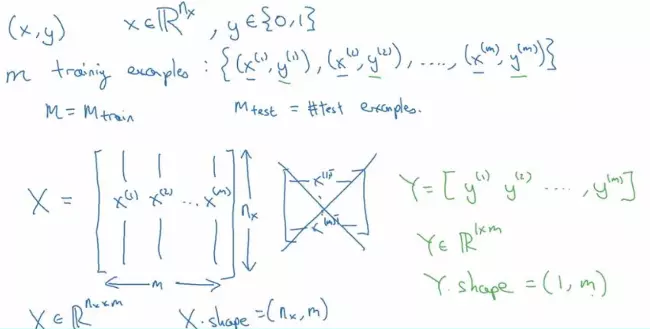
Chữ viết hoa đại diện cho ma trận vi dụ Z, A, X, Y,...
m : số lượng ví dụ để học tập
(x,y) là một ví dụ học tập. Trong đó x là 1 vector kích thước ( nx, 1), y thuộc {0,1}
X là ma trận features gồm m vector x đặt cạnh nhạu sẽ có kích thước (nx, m)
Y là ma trận đâu ra của m ví dụ dụ học tập kích thước (m, 1) Tổng quan sẽ như sau:

Chi tiết hơn bạn có thể xem ở đây

Binary Classification

Trong vấn đề phân loại nhị phân, chúng ta có đầu vào x, giả sử đó là một hình ảnh và chúng ta phải phân loại đó có phải là hình ảnh mèo không ? Nếu đúng gán là 1, ngược lại gán là 0. Ở đây có 2 giá trị đầu ra, vì vậy đây là một ví dụ về phân loại nhị phân. Với bài toán này, chúng ta sử dụng kỹ thuật phổ biến nhất - hồi quy logistic ( logistic regression).

Logistic Regression

Cho đầu vào X (image) và xuất ra xác suất hình ảnh thuộc lớp 1 (hình ảnh mèo). Đối với đầu vào là một vecor x thì đâu ra của nó theo hồi quy tuyến tính sẽ là:

$y = w^{T}x + b$

Với w, x là các tham số, w. Vì đầu ra y ta cần là xác suất nên nó nằm trong khoảng từ 0 đến 1, nhưng với phương trình trên nó có thể cho ra bất kỳ số thực nào. Vì vậy, hồi quy logistic sử dụng hàm sigmoid để đưa ra xác xuất đầu ra:

$\hat{y} = \sigma(w^{T}x + b)$

Với bất kì giá trị nào, hàm sigmoid sẽ đưa ra giá trị từ 0 đến 1. Công thức hàm sigmoid như sau:

$\sigma(z)= \frac{1}{1 + e^{z}}$

Vì vậy, nếu z rất lớn, exp (-z) sẽ tiến tới 0 và do đó, đầu ra của sigmoid sẽ là 1. Tương tự, nếu z rất nhỏ, exp (-z) sẽ ra vô cùng và do đó đầu ra của sigmoid sẽ là 0. Lưu ý rằng, w là một vector có nx chiều và b là một số thực. Bây giờ ta xem xét hàm chi phí của hồi quy logicstic.

Logistic Regression Cost Function

Để huấn luyện các tham số w và b của hồi quy logistic, chúng ta cần một hàm chi phí. Ta muốn tìm các tham số w và b sao cho ít nhất trên tập huấn luyện, các đầu ra ta có (y-hat) gần với các giá trị thực tế (y).

Nếu như trong linear regression (hồi quy tuyến tính) ta có hàm mất loss function) như sau:

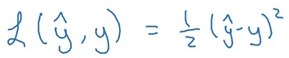
Nếu chúng ta cố gắng sử dụng hàm chi phí của hồi quy tuyến tính trong 'Hồi quy logistic' thì sẽ không có ích gì vì cuối cùng nó sẽ là một hàm không lồi với nhiều mức tối thiểu cục bộ, trong đó rất khó để giảm thiểu giá trị chi phí và tìm mức tối thiểu toàn cầu. Vì vậy, đối với hồi quy logistic, chúng ta xác định một hàm mất khác có vai trò tương tự như hàm mất ở trên và cũng giải quyết vấn đề tối ưu hóa bằng cách đưa ra hàm lồi:

Để tìm hiểu tại sao lại có hàm này bạn có thể tham khảo tại đây hoặc tại đây. Hàm mất mát trên chỉ định nghĩa cho một ví dụ đào tạo duy nhất. Mặt khác, một hàm chi phí dành cho toàn bộ tập huấn luyện (bộ training - hay bộ học). Hàm chi phí cho hồi quy logistic là:

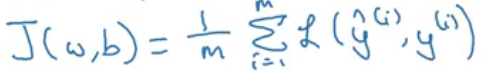
Chúng ta muốn giá trị hàm trị phí càng nhỏ càng tốt, vì vậy chúng ta muốn tìm được w, b để tối ưu hóa hàm trên.

Gradient Descent

Đây là một kĩ thuật quen thuộc trong machine learning để tìm được các giá trị w, b làm cho hàm chí phí đạt giá trị cực tiểu. Hàm chi phí cho hồi quy logistic có bản chất lồi (tức là chỉ có một cực tiểu toàn cầu) và đó là lý do để chọn hàm này thay vì hàm lỗi bình phương (có thể có nhiều cực tiểu cục bộ). Chúng ta hãy xem các bước gradient Descent (giảm dốc):

Khởi tạo w và b (thường được khởi tạo nhỏ gần 0 )
Bước một bước theo hướng xuống dốc nhất
Lặp lại bước 2 cho đến khi đạt được tối ưu toàn cầu

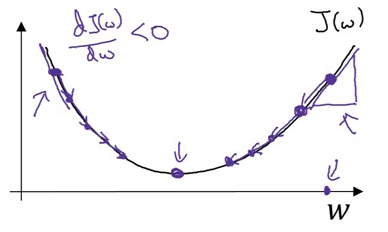
Phương trình cập nhật cho gradient desent trở thành:

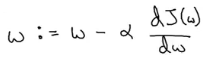
Ở đây, ⍺ là learning rate kiểm soát độ lớn của bước nhảy khi ta xuống dốc.

Nếu chúng ta ở phía bên phải của biểu đồ hiển thị ở trên, độ dốc sẽ dương. Sử dụng phương trình cập nhật, chúng ta sẽ di chuyển sang trái (tức là hướng xuống) cho đến khi đạt cực tiểu toàn cầu. Trong khi đó, nếu chúng ta ở phía bên trái, độ dốc sẽ âm và do đó chúng ta sẽ tiến một bước về phía bên phải (hướng xuống) cho đến khi đạt được cực tiểu toàn cầu. Khá trực quan, phải không các bạn?

Các phương trình cập nhật cho các tham số của hồi quy logistic là: Nhưng tính các đạo hàm trên như nào? Chúng ta hãy xét các ví dụ sau để tìm hiểu cách tìm các đạo hàm từng phần để cập nhật các trọng số.

Computation Graph

Những đồ thị này tổ chức tính toán của một chức năng cụ thể. Hãy xem xét ví dụ sau: J(a,b,c) = 3(a+bc).

Chúng ta phải tính J theo a, b và c. Chúng ta có thể chia điều này thành 3 bước:

u = bc
v = a + u
J = 3v

Với a = 5, b = 3 và c = 2 ta có đồ thị tính toán như sau: Đây chính là lan truyền về phía trước (forward propagation) để cho ra output J. Chúng ta cũng sẽ sử dụng chính biểu đồ này để thực hiện làn truyền ngược (backward propagation) hay chính là bược tính đạo hàm để cập nhật các trọng số a, b, c.

Derivatives with a Computation Graph

Bây giờ hãy xem làm thế nào chúng ta có thể tính toán các đạo hàm với sự trợ giúp của biểu đồ tính toán. Giả sử chúng ta phải tính dJ / da. Các bước sẽ là:

Vì J là hàm của v, nên tính dJ / dv:

$\frac{\mathrm{d} J}{\mathrm{d} v} = \frac{\mathrm{d} 3v}{\mathrm{d} v} = 3$
Vì v là hàm của a và u, nên tính dv / da:

$\frac{\mathrm{d} v}{\mathrm{d} a} = \frac{\mathrm{d} (a+u)}{\mathrm{d} a} = 1$
Tính dJ / da:

$\frac{\mathrm{d} J}{\mathrm{d} a} = \frac{\mathrm{d} J}{\mathrm{d} v} * \frac{\mathrm{d} v}{\mathrm{d} a}$

Tương tự, chúng ta có thể tính toán dJ / db và dJ / dc.

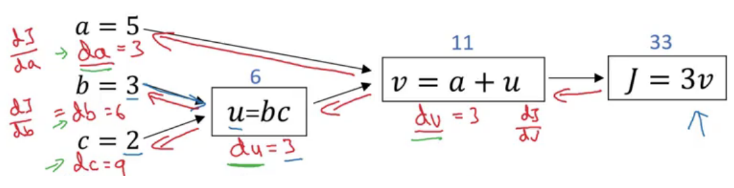
Chú ý là trong hình trên da = dJ/ da, db = dJ/db, dv = dJ/dv

Bây giờ bạn đã hiểu cơ bản về các khối tính toán và gradient descent như thế nào rồi? Chúng ta sẽ tìm hiểu về các cập nhật các trọng số trong hồi quy logistic như thế nào.

Logistic Regression Gradient Descent

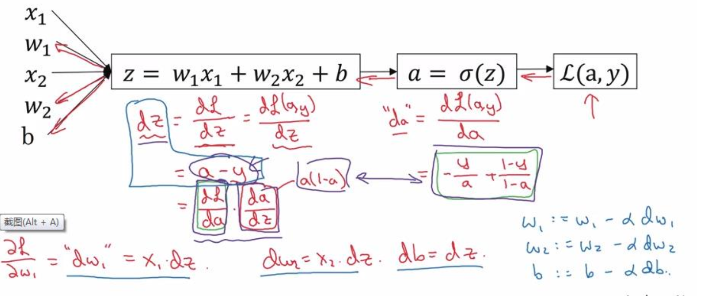
Ta có tóm tắt các phương trình trong hồi quy logistic như sau: Với L là loss function (hàm mất mát). Giả sử ta có 2 đặc tính x1, x2 biểu đồ tính toán để tính toán tổn thất sẽ là:

Ở đây, các parameter (trọng số) cần cập nhật bao gồm w1, w2 và b. Dưới đây là các bước cập nhật w1:

Tính da:

$da = \frac{\mathrm{d} L}{\mathrm{d} a} = \frac{-y}{a} + \frac{1-y}{1-a}$
Tính dz:

$dz = \frac{\mathrm{d} L}{\mathrm{d} z} = \frac{\mathrm{d} L}{\mathrm{d} a} * \frac{\mathrm{d} a}{\mathrm{d} z} = (\frac{-y}{a} + \frac{1-y}{1-a}) * a(1-a) = a - y$
Tính dw1:

$dw1 = \frac{\mathrm{d} L}{\mathrm{d} w1} = \frac{\mathrm{d} L}{\mathrm{d} a} * \frac{\mathrm{d} a}{\mathrm{d} z} * \frac{\mathrm{d} z}{\mathrm{d} w1} = (a - y) * \frac{\mathrm{d} z}{\mathrm{d} w1}$

Nếu bạn thắc mắc vì sao da/ dz = a(1-a), có thể chứng minh như sau:

Cách cập nhật w2 và b tương tự. Ta có bức tranh tổng quát như sau:

Gradient Descent on ‘m’ Examples

Chúng ta định nghĩa hàm chi phí cho m ví dụ đào tạo như sau:

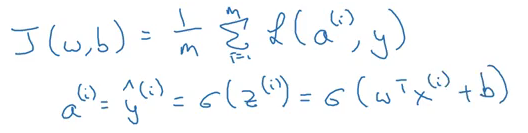
Ta cũng có đạo hàm của hàm mất mát như sau: Bây giờ chúng ta sẽ xem tổng quát bằng code :

J = 0; dw1 = 0; dw2 =0; db = 0;                
w1 = 0; w2 = 0; b=0;                            
for i = 1 to m
    # Forward pass
    z(i) = W1*x1(i) + W2*x2(i) + b
    a(i) = Sigmoid(z(i))
    J += (Y(i)*log(a(i)) + (1-Y(i))*log(1-a(i)))
    
    # Backward pass
    dz(i) = a(i) - Y(i)
    dw1 += dz(i) * x1(i)
    dw2 += dz(i) * x2(i)
    db  += dz(i)
J /= m
dw1/= m
dw2/= m
db/= m

# Gradient descent
w1 = w1 - alpa * dw1
w2 = w2 - alpa * dw2
b = b - alpa * db

Nhưng nhìn như trên có vẻ dài dòng và không hiểu quả ? Làm thế nào để code gọn và hiệu quả hơn ?

Vectorization

Vectorization về cơ bản là một cách để loại bỏ các vòng lặp trong code của chúng ta. Nó thực hiện tất cả các hoạt động cùng nhau cho các ví dụ đào tạo 'm' thay vì tính toán chúng riêng lẻ. Chúng ta hãy xem xét biểu diễn non-vectorized và vectorized của hồi quy logistic:

z = 0
for i in range(nx):
   z += w[i] * x[i]
z +=b

Bây giờ chúng ta sẽ sử dụng vectorized, với đâu vào w, x biểu diễn dưới dạng vector như sau: Bây giờ chúng ta có thể tính Z cho tất cả các ví dụ đào tạo bằng cách sử dụng thư viện numpy trong python, thư viện này rất mạnh trong tính toán ma trận:

import numpy as np
Z =  Z = np.dot (W, X) + b

Bây giờ, hãy xem làm thế nào chúng ta có thể vectorize toàn bộ thuật toán hồi quy logistic.

Vectorizing Logistic Regression

Thay vì dùng 1 vòng for để chạy hết m ví dụ thì ta chỉ cần 1 câu lệnh đơn giản để tính Z:

#np.dot là tích vô hướng của 2 ma trận
Z = np.dot(W.T, X) + b

Ở đây, X chứa các tính năng cho tất cả các ví dụ đào tạo trong khi W là ma trận hệ số cho các ví dụ này. Bước tiếp theo là tính toán đầu ra (A) là sigmoid của Z:

A = 1 / 1 + np.exp(-Z)

Bây giời chúng ta sẽ tính mất mát và sử dụng lan truyền ngược (backpropagation) để tối thiểu hàm mất mát (loss function):

dz = A – Y

Cuối cùng chúng ta sẽ đọa hàm các tham số và cập nhất chúng như sau:

dw = np.dot(X, dz.T) / m

db = dz.sum() / m

W = W – ⍺dw

b = b – ⍺db

A note on Python/Numpy Vectors

Nếu chúng ta tạo một mảng 1 chiều bằng câu lệnh sau:

a = np.random.randn (5)

Nó sẽ tạo ra một mảng hình dạng (5,) là mảng rank 1. Sử dụng mảng này sẽ gây ra vấn đề trong khi lấy chuyển vị của mảng. Thay vào đó, chúng ta có thể sử dụng đoạn mã sau để tạo thành một vectơ thay vì mảng rank 1:

a = np.random.randn(5,1)    # vector cột kích thước (5, 1)

a = np.random.randn(1,5)    # vector hàng kích thước (1, 5)

Để chuyển đổi một vectơ hàng (1,5) thành một vectơ cột (5,1), ta có thể sử dụng:

a = a.reshape ((5,1))

Reference

Tuần 2 khóa học Nerual Network and Deep Learning

Các slide của tuần 2 khóa học trên tại đây

Kết luận

Bài viết đến đây đã dài, cảm ơn các bạn đã đọc hết đến phần cuối này. Nếu bài viết hay, hi vọng các bạn để lại comment, voteup và share. Hẹn gặp các bạn ở bài viết tiếp theo.

Deep Leanring