Algorithm Introduction

In a multiprogramming environment, several threads may compete for a finite number of resources. A thread requests resources; if the resources are not available at that time, the thread enters a waiting state. Sometimes, a waiting thread can never again change state, because the resources it has requested are held by other waiting threads. This situation is called a deadlock. Generally speaking, we can deal with the deadlock problem in one of three ways:

• We can ignore the problem altogether and pretend that deadlocks never occur in the system. Called Deadlock Prevention.
• We can use a protocol to prevent or avoid deadlocks, ensuring that the system will never enter a deadlocked state. Called Deadlock Avoidance.
• We can allow the system to enter a deadlocked state, detect it, and recover. Called Deadlock Dectection & Recovery.

Data structure for algorithm

1. m: the number of resource types. Resource types include $R_{1},R_{2},...,R_{m}$
2. n: the number of threads. Threads are $P_{1},P_{2},...,P_{n}$
3. Available: the vector of length m indicates the number of available resources of each type. For example, if $Available[j] = k$, then $k$ instances of resource type $R_{j}$ are available.
4. Max: An $n \times m$ matrix defines maximum demand of each thread. If $Max[i][j] = k$, then thread $P_{i}$ request at most k instances of resource type $R_{j}$.
5. Allocation: An $n \times m$ matrix defines the number of resources of each type currently allocated to each thread. If $Allocation[i][j] = k$, then thread $P_{i}$ is currently allocated k instances of resource type $R_{j}$.
6. Need: An $n \times m$ matrix indicates the remaining resource need of each thread. If $Need[i][j] = k$, then thread $P_{i}$ may need $k$ instances of resource type $R_{j}$ to complete its task. Note that $Need[i][j] = Max[i][j] - Allocation[i][j]$.

What is Resource-Allocation State?

Resource-Allocation State is defined by the number of instances of resources :

• available in the system
• allocated for threads
• maximum for each thread

For example:
Suppose that, system has 12 resources. At time $t_{0}, Allocation(P_{0},P_{1},P_{2}) = (5,2,2)$, $Available = 12 - (5+2+2) = 3$ resources.

At time $t_{0}$, system is in safe state. Because, the sequence $<P_{1},P_{0},P_{2}>$ satifies the safety condition. With $Available = 3$ thread $P_{1}$ can immediately be allocated all its resources and then return them, $Available = 3 + 2 = 5$; then thread $P_{0}$ can get all its resources and return them, $Available = 5 + 5 = 10$; and finally thread T2 can get all its resources and return them.
Suppose that, at time $t_{1}$ ,thread $P_{2}$ requests and is allocated one more resource. At this point, only thread $P_{1}$ can be allocated all its resources. When it returns them, the system will have only four available resources. Since thread P_{0) is allocated five resources but has a maximum of ten, it may request five more resources. If it does so, it will have to wait, because they are unavailable. Similarly, thread $P_{2}$ may request six additional resources and have to wait, resulting in a deadlock. In this case, system go from safe state to unsafe state.

Safety algorithm

In this algorithm, we use vector. Consider vector X and Y. We say $X<=Y$ if and only if $X[i] <= Y[i]$ for all $i=1,2,...,n$. Each row of $Max,Need,Allocation$ is a vector.

Safety algorithm check current state: safe or unsafe? OR pseudo code:

Bool Safe(Current Resource-Allocation State) {
    Work <- Available;
    for(i: 1 -> n) Finish[i] = false;
    flag <- true;
    While(flag) {
        flag <- false;
        for(i: 1 -> n) {
            if(Finish[i] = false AND Need[i] <= Work) {
                finish[i] = true;
                Work <- Work + Allocation[i];
                flag = true;
            }//endif
        }//endwhile
        
        for(i: 1->n) if(finish[i] = false) return false;
        return true;
    }
}

Resource-Request Algorithm

Data Structure:
Request[i]: the request resource vector for thread $P_{i}$. If $Request[i][j] = k$ then, thread $P_{i}$ wants $k$ instances of resource type $R_{j}$.

Pseudo Code:

Void Resource-Request-Handling(Request[i]) {
    if(Request[i] > Need[i])
        Error; // has exceeded its maximum claim
    if(Request[i] > Available)
        Block; // don't enough, wait
    
    // Setup new state
    Available = Available - Request[i];
    Allocation[i] = Allocation[i] + Request[i];
    Need[i] = Need[i] - Request[i];
    
    // check safe or unsafe
    if(Safe(New Resource-Allocation State)) {
        Allocate(P[i]); // thread P[i] is allocated its resources
    }
    else {
        wait(P[i]); // P[i] wait
        
        // restore old state
        Available = Available + Request[i];
        Allocation[i] = Allocation[i] - Request[i];
        Need[i] = Need[i] + Request[i];
    }
}

Practice exercise

Consider the following snapshot of a system:

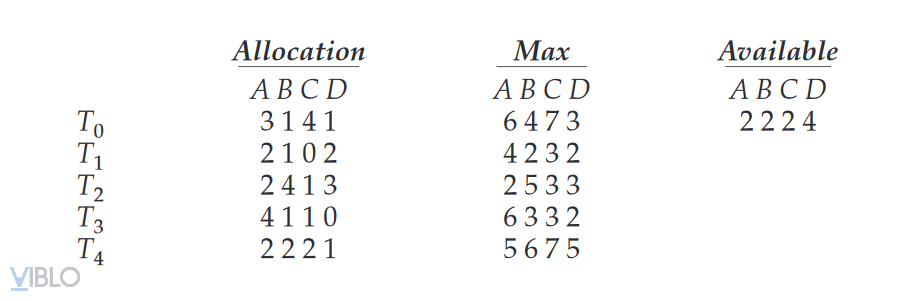
1. Illustrate that the system is in a safe state by demonstrating an order in which the threads may complete.
2. If a request from thread $T_{4}$ arrives for $(2, 2, 2, 4)$, can the request be granted immediately?

Solution:

1. The content of $Need$ matrix is difined to be $Max - Allocation$ and is as follow:

This sequence of thread $<T_{2}, T_{3},T_{4}, T_{0}, T_{1}>$ satisfies the safety criteria. This state is safe.

2. $Request[4] = (2,2,2,4) \leq Need[4] AND Request[4] = (2,2,2,4) \leq Available.$ New state: $Available = Available-Request[4] = (0,0,0,0) \Rightarrow$ unsafe$\Rightarrow Request[4]$ can't be granted immediately.

References.

1. Abraham Silberschatz - Operating System Concepts 10th 2018
2. Silde Chapter 2 - Thread Manage - Operating System, SoICT, HUST