2-5 GROUP BY và PARTITION BY
Bài đăng này đã không được cập nhật trong 4 năm
2-5 GROUP BY và PARTITION BY
Trong những chức năng mà SQL có thì có GROUP BY và PARTITION BY là hai chức năng có hoạt động khá giống nhau, mà cũng có thể nói là giống nhau cũng được. Và cả hai câu lệnh đều mang cơ sở mang tính toán học. Tại chương này sẽ lấy key là mội khái niệm quan trọng trong luận tập hợp là loại để giải thích rõ ràng ý nghĩa của GROUP BY và PARTITION BY mang.
Khi tiến hành những thao tác đối với dữ liệu thì một trong những thao tác cơ bản đó chusnh là phân loại dữ liệu thành từng nhóm theo một cơ sở nào đó. Không chỉ những khi sử dụng SQL mà trong cuộc sống thường ngày cũng có những khi muốn điều tra, chỉnh lý lại dữ liệu thì chúng ta cũng hay thực hiện tác nghiệp là phân loại nhóm dữ liệu.
Trong những câu lệnh của SQL thì thứ có chức năng để phân nhóm đó chính là GROUP BY và PARTITION BY. Cả hai câu lệnh này đều thực hiện động tác phân loại theo key được chỉ định. Cái khác là trong trường hợp GROUP BY thì sau khi phân loại sẽ tiến hành thao tác tập hợp lại thành một dòng.
Ví dụ chúng có lấy một bảng hiển thị cấu trúc một vài đội chơi như sau.
Teams
| member | team | age |
|---|---|---|
| Ooki | A | 28 |
| Tanaka | A | 19 |
| Shindo | A | 23 |
| Yamada | B | 40 |
| Kumoto | B | 29 |
| Hashida | C | 30 |
| Nonomiya | D | 28 |
| Onizuka | D | 28 |
| Kato | D | 24 |
| Shinjo | D | 22 |
Nếu chúng ta sử dụng GROUP BY và PARTITION BY đối với bảng này thfi có thể viết được truy vấn để có được thông tin trên đơn vị đội. Kể cả sử dụng câu lệnh nào đi chăng nữa thì chúng ta sẽ thực hiện đối với những bộ phận tập hợp đã chia ra những thao tác như dùng hàm số SUM để tính tổng rồi dùng hàm RANK để xếp hạng.
SELECT member, team, age
RANK () OVER(PARTITION BY team ORDER BY age DESC) rn,
DENSE_RANK () OVER(PARTITION BY team ORDER BY age DESC) dense_rn,
ROW_NUMBER () OVER(PARTITION BY team ORDER BY age DESC) row_num
FROM Members
ORDER BY team, rn;
Kết quả
member team age rn dense_rn row_num
------- ----- --- -- -------- --------
Ooki A 28 1 1 1
Shindo A 23 2 2 2
Tanaka A 19 3 3 3
Yamada B 40 1 1 1
Kumoto B 29 2 2 2
Hashimoto C 30 1 1 1
Nonomiya D 28 1 1 1
Onizuka D 28 1 1 1
Kato D 24 3 2 3
Shinjo D 22 4 3 4
Nếu nhìn partition cut bằng hình ảnh thì ta sẽ có
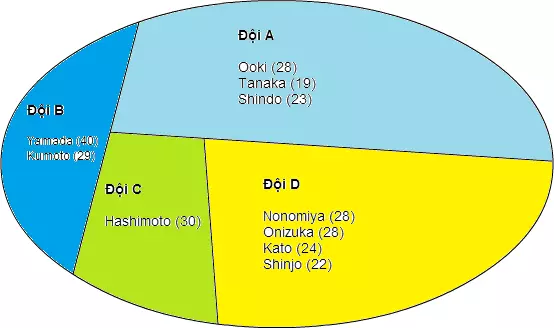
Bình thường thể hiện tập hợp bằng các hình tròn là điều thông thường, chương này và cũng như những chương khác cũng như vậy, tại đây để hình dung được hình ảnh thao tác "cut" thì chúng ta biểu hiển bằng việc cắt thành những tập hợp bộ phận bằng những đường thẳng.
Tại đây, chú ý vào những tập hợp bộ phận được chia thì chúng ta có thể thấy được ba tính chất như sau,
- Ít nhất không có tập hợp rỗng
- Tổng các tập hợp bộ phận bằng với tập hợp trước khi phân chia
- Không có tập hợp bộ phận nào có bộ phận giao
Chúng ta phân chia các tập hợp bộ phận từ chính dãy team tồn tại trong bảng ban đầu nên chắc chắn không thể có tập hợp rỗng trong tập hợp sau khi phân chia. (Cũng có thể có tập hợp có bao gồm NULL nhưng đó là một loại khác so với tập hợp rỗng. Trong toán học thì trong trường hợp tập hợp ban đầu là tập hợp rỗng thì tập hợp rỗng cũng là 1 loại nên sau khi chạy GROUP BY của SQL thì chương trình vẫn chạy thông thường và kết quả sẽ ra tập hợp rỗng.) Mặt khác thì nếu cộng tất cả những tập hợp bộ phận sau khi phân chia mà ra tập hợp mẹ ban đầu thì đó gần như là một điều đương nhiên, nếu nói một cách khác thì không có thành viên nào đi lạc cả.
Mặt khác, cũng không có thành viên nào cùng thuộc cả 2 tập hợp bộ phận (hoặc nhiều tập hợp bộ phận). Một thành viên nhất định sẽ được chia vào một tập hợp. Có nghĩa rằng chúng ta có thể hiểu GROUP BY và PARTITION BY là hàm số để chia các thành viên thích hợp vào các đội.
Trong toán học, những tập hợp bộ phận thoả mãn 3 điều kiện trên thì được gọi là partition (phần). Cái tên PARTITION BY trong SQL cũng bắt nguồn từ nguồn gốc này. mặt khác cũng có thể đặt cái tên này cho GROUP BY nhưng trong trường hợp của GROUP BY thì sau khi cut thì chắc chắn sẽ có thao tác tập hợp lại thêm vào nên chắc để tránh nhầm lẫn thì người ta dùng một cái tên khác. Thông thường có rất nhiều phương pháp để phân loại một tập hợp thành các phần. Trong SQL thì chỉ cần thay GROUP BY và PARTITION BY là nhóm được tạo ra cũng khác nhau.
Cũng như chúng ta có thể thấy rằng GROUP BY được sử dụng rất nhiều xung quanh, thì trong cuộc sống bình thường, xung quanh chúng ta tồn tại rất nhiều phần. Ví dụ, những lớp trong một trường hay quê quán mình xuất thân. Chả có ý nghĩa gì khi tạo ra một lớp mà không có học sinh hay cũng chả có ai được sinh ra ở 2 tỉnh. (Có thể có những người sinh ra mà không biết quê quán của mình ở đâu, trong trường hợp đó thì sẽ vào phần có key là NULL).
Hoặc, các lá bài trong bộ bài cũng vậy. Trong 52 lá bài thì dựa theo kí hiệu được kí hiệu trên từng lá bài thì chúng ta có thể chia thành 4 nhóm hay cũng có thể chia thành hai nhóm theo màu là đen và đỏ. Những thành phần cùng ở trong một phần với ý nghĩa ucngf thoả mãn một cơ sở chung nào đó. (Trong toán học thì người ta gọi đây là quan hệ đồng giá trị)
Ở đây, thông qua cách phân loại mả từng phần có những tên gọi khác nhau. Có rất nhiều phần có những đặc trưng thú vị nhưng trong đó có một thứ gọi là "phần dư". Cũng như tên của nó thì đây là phần được chia vào phần dư của số nguyên. (Thông thường thì không cần thiết giới hạn số lượng tập hợp trong phần nhưng ở đây mọi người hãy nghĩ chỉ là những số thông thường).
Ví dụ, khi phân loại những số tự nhiên (N) theo số dư sau khi chia cho 3 thì ta có
Chia cho 3 dư 0: M1 = {0,3,6,9,...} Chia cho 3 dư 1: M2 = {1,4,7,10,...} Chia cho 3 dư 2: M3 = {2,5,8,11,...}
Nếu theo tính chất thứ 2 của partition thì chúng ta có 3 tập hợp bộ phận này nối với nhau sẽ được tập hợp số tự nhiên. Nếu viết bằng công thức thì chúng ta sẽ có
M1 + M2 + M3 = N
Hàm số chia ở đây chính là MOD. Trong SQL thông thường sẽ không tồn tại hàm số này nhưng hầu hết có thể sử dụng trong các DBMS. Nếu viết bằng SQL thì chúng ta có thể viết như sau chăng.
---Phân loại theo số dư sau khi chia cho 3 của các số 1~10
SELECT MOD(num, 3) AS modulo,
num
FROM Natural
ORDER BY modulo, num;
Kết quả
modulo num
------ ----
0 0
0 3
0 6
0 9
1 1
1 4
1 7
1 10
2 2
2 5
2 8
Phần dư này cũng mang những tính chất khá thú vị nên cũng có nhiều ứng dụng. Để nêu lên một ví dụ, phần dư sẽ phân loại tập hợp số tự nhiên ban đầu thành những phần có kích thước giống nhau nên lấy mẫu bằng một tỷ lệ đặc định sẵn từ một khối lượng dữ liệu lớn thì rất tiên lợi. Ví dụ nếu sử dụng truy vấn sau thì có thể giảm xuống được 1/5 lượng dữ liệu (Trong trường hợp trong bảng không có dãy thứ tự thì chúng ta có thể sử dụng ROW_NUMBER để gán số cho dãy cũng có thể được)
--Lấy 1/5 số dòng từ bảng ban đầu
SELECT *
FROM SomeTbl
WHERE MOD(seq, 5) = 0;
--Ngay cả trong trường hợp trong bảng không có dãy số thứ tự thì có thể dùng hàm số ROW_NUMBER
SELECT *
FROM (SELECT col,
ROW_NUMBER() OVER(ORDER BY col) AS seq
FROM SomeTbl)
WHERE MOD(seq, 5) = 0;
Tất nhiên trong thực tế không hẳn chắc chắn số dòng sẽ chia hết cho 5 nên không hẳn số thành phần trong một phần sẽ giống nhau nuhwng đối với yêu cầu lấy mẫu ngẫu nhiên với điều kiện phân chia tập hợp thành những phần bằng nhau mà không đụng gì đến dữ liệu thì cũng coi như thoả mãn.
Mọi người thấy như thế nào? Không biết mọi người đã nâng cao thêm những kiến thức của mình về cơ sở mang tính toán học của hình ảnh động tác của GROUP BY và PARTITTION BY chưa? Như thế này, đây là thành quả rất hay được đưa vào trong bản phát triển của luận tập hợp hay luận về nhóm của SQL và cơ sở dữ liệu quan hệ.
Đây là một câu chuyện có thể mọi người sẽ cảm thấy nó hơi trừu tượng, mà chính xác là nó có tính trừu tượng nhưng nó đảm bảo tính ứng dụng cao. Những lý luận của toán học không chỉ là trò đùa vui xa rời thực tế mà nó chứa trong đó khả năng ứng dụng lớn đối với các nghiệp vụ trong thực tế. Nhưng đó không phải là thứ có thể nhìn thấy nếu chỉ chờ đợi. Tác giả nghĩ rằng bằng sự cố gắng làm cầu nối giữa nguyên lý và thực tiễn như một kĩ sư năng động thì có thể nâng cao thêm được năng lực ứng dụng của chính mình.
All rights reserved