Đã đăng vào thg 5 9, 2020 10:26 SA 9 phút đọc

2.0K

Xây dựng mô hình dự đoán tình trạng COVID-19 đơn giản với Python

Bài đăng này đã không được cập nhật trong 4 năm

Trong mùa dịch COVID-19, mình được giao một bài tập nho nhỏ về sử dụng hàm gia tăng dân số và áp dụng vào số liệu của COVID-19. Sau bài tập đó mình bắt đầu tìm hiểu sâu hơn để tăng độ chính xác của hàm dự đoán, vì mình vẫn cảm thấy mình có thể làm khớp hơn được nữa. Vậy nên mình quyết định viết 1 bài nho nhỏ để chia sẻ những gì mình đã tìm được

Sau đây là những ý chính trong bài của mình:

Sơ lược về hàm gia tăng dân số
Tìm kiếm dữ liệu
Dự đoán
Tối ưu độ chính xác
Nhận xét

1. Sơ lược về hàm gia tăng dân số

Với các bạn cấp 3, chắc hẳn ai cũng biết rằng hàm gia tăng dân số là hàm mũ. Đó là bởi vì đạo hàm của nó tỉ lệ với chính nó, hay nói cách khác:

$\frac{dP}{dt} = \alpha.P$

Kết quả của phương trình trên sẽ là $P=e^{\alpha.t}$
Nhưng trong thực tế, mọi quần thể sinh vật đều không hoàn toàn tăng theo quy luật đó, bởi vì lượng tài nguyên của môi trường là có hạn, nghĩa là số lượng sẽ đạt cực đại tại một giá trị nào đó phụ thuộc vào môi trường sống. Đó chính là khái niệm của đường tăng trưởng trong Sinh học.
Với bài tập của mình, mình được giao sử dụng công thức này để tính mức độ tăng trưởng:

$\frac{dP}{dt} = \alpha.P\left(1-\frac{P}{cap}\right)\text{ (1)}$

Trong đó, $cap$ chính là giới hạn của quần thể trong môi trường.
Với hàm này, mình thấy rằng nếu $P << C$ thì $\frac{dP}{dt} \approx\alpha.P$ . Và khi $P\approx C$ , $\frac{dP}{dt} \approx 0$ . Nghĩa là nó hoàn toàn mô tả đường tăng trưởng mà mình đang nói tới, tăng nhanh khi quần thể còn nhỏ so với môi trường và dần dần ngừng tăng trưởng khi đã đạt giới hạn môi trường.
Đặt $a=-\frac{\alpha}{cap}, b=\alpha$ ,

$(1)\Leftrightarrow \frac{1}{P}.\frac{dP}{dt} = aP + b$

Mình hoàn toàn có thể tìm được $a$ , $b$ bằng thư viện linear_model trong scikit-learn.

from sklearn import linear_model
reg = linear_model.LinearRegression()
reg.fit(X, Y)
a = reg.coef_[0]
b = reg.intercept_

Sau đó, giải phương trình $(1)$ để tìm hàm $P$

$P = \frac{b .e^{b.t}}{C - a.e^{b.t}}$

Khi đó,

$C = \frac{b .e^{b.t}}{P} + a.e^{b.t}$

Để tìm được C tối ưu nhất với bộ dữ liệu, cần phải dùng nhiều phương pháp phức tạp. Nhưng mình nghĩ sự khác biệt sẽ không rõ ràng lắm, thế nên mình chỉ thay các cặp dữ liệu $(t, P[t])$ tương ứng để chọn ra C tốt nhất.

2. Tìm kiếm dữ liệu

Hiện tại mình thấy rằng worldometer cập nhật thông tin khá chính xác và nhanh chóng, nên mình sẽ tìm cách để lấy dữ liệu trên trang này. Như mình thấy, trang không hề request dữ liệu tới server, nghĩa là dữ liệu đã được gắn vào thẻ <script> và render tại server.

Mình sẽ sử dụng thư viện pyQuery để crawl html của trang web và tìm cách lấy data trong thẻ script đó:

from pyquery import PyQuery as pq
base = "https://www.worldometers.info/coronavirus/country/"
country = "viet-nam"
d = pq(url=base + country)
data = d(".col-md-8").eq(2).find("script").eq(0).__str__()
start = data.index("data") + 6
end = data.index("]", start) + 1
data = data[start:end]
P = json.loads(data)

Sau đó mình sẽ dùng mảng P để tính mảng dP $(\frac{dP}{dt})$ và re_dP $(\frac{1}{P}.\frac{dP}{dt})$ để tìm hệ số cho hàm dự đoán.

3. Dự đoán

Sau khi đã hoàn thiện hàm dự đoán, mình sẽ plot nó ra cùng với dữ liệu thực tế để xem nó "khớp" tới mức nào.
Phần code đầy đủ mình sẽ để ở cuối bài

import numpy as np
import matplotlib.pyplot as plt

n = len(P)

def calculate_P(t, C):
  return (b / (np.exp((-b * t + C) / 2) - a)) ** 2

def calculate_C(t, P):
  if P == 0:
    P = 0.01
  return 2 * np.log(b/np.sqrt(P) + a) + b * t

def find_best_C():
  res = -1
  best_C = calculate_C(0, P[0])
  pos = 0
  for i in range(1, n):
    C = calculate_C(i, P[i])
    s = 0
    for j in range(n):
      _P = calculate_P(j, C)
      s += np.abs(P[j] - _P)
    if res == -1 or res > s:
      res = s
      best_C = C
      pos = i
  return best_C, pos

C, _ = find_best_C()

X = np.linspace(0, n * 2, n * 100)
Y = calculate_P(X, C)
plt.plot(X, Y, "b-", label="P", markerSize=1)
xP = np.linspace(0, n - 1, n)
plt.plot(xP, P, "bo", label="scatter P")
plt.grid(axis='both', color='0.95')
plt.show()

Mình thử với dữ liệu của 2 nước Ý và Mỹ

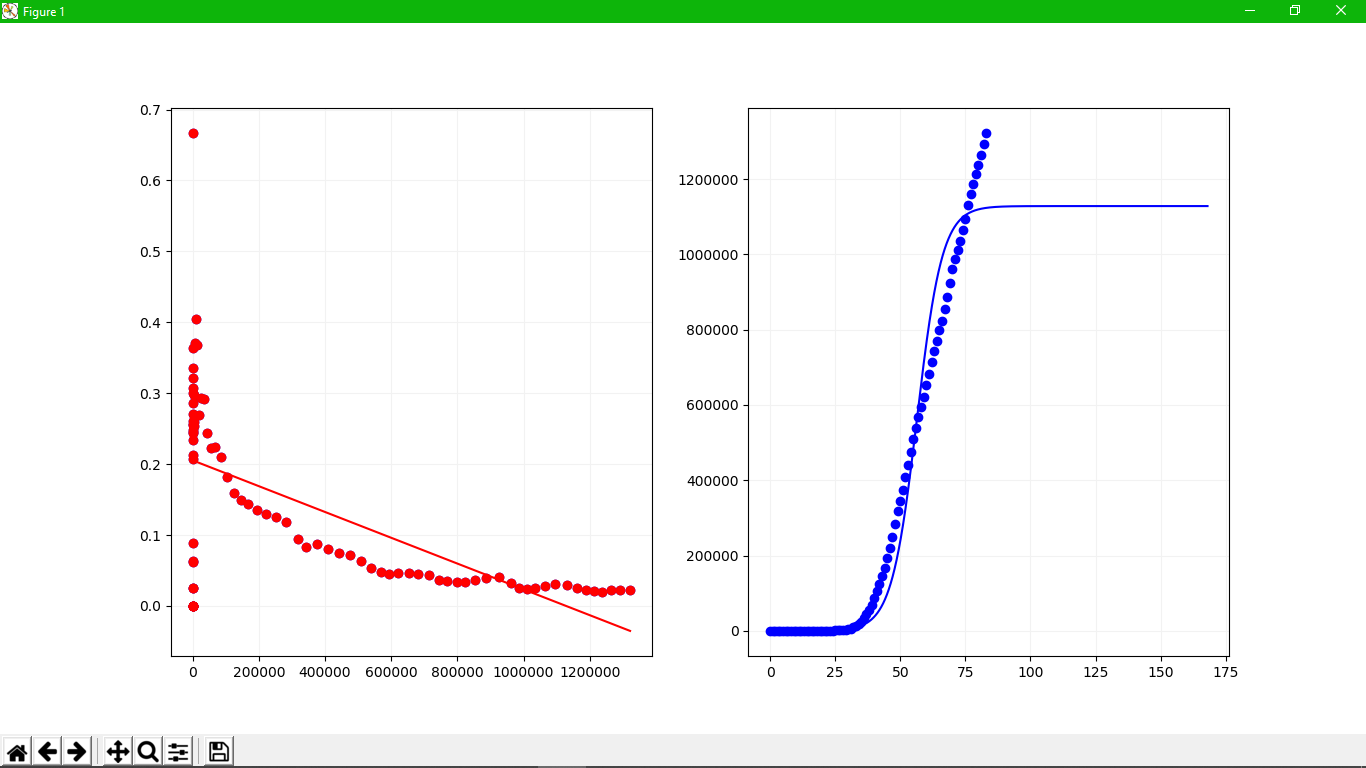
Đồ thị bên trái là plot của hàm tốc độ tăng tương đối $\frac{1}{P}.\frac{dP}{dt}$ và bên phải là plot của hàm dự đoán $P$ .
Như các bạn thấy đấy, nó nhìn chả ra sao cả, bởi vì ngay từ hàm tốc độ tăng tương đối không phản ảnh chính xác thực tế.

4. Tối ưu độ chính xác

Qua kết quả bước đầu, mình thấy một vài vấn đề xảy ra đã khiến cho hàm dự đoán không thể đánh giá chính xác:

Hàm tốc độ tăng tương đối giảm quá nhanh so với thực tế
Các giá trị đầu của hàm tốc độ tăng tương đối không đi theo với xu hướng nên gây nhiễu mạnh

Hàm tốc độ tăng tương đối giảm nhanh

Sau khi thử nghiệm nhiều hơn với dữ liệu của nhiều nước, mình nhận thấy xu hướng chung của hàm này không phải là tuyến tính. Thế nên mình đã thử nghiệm một vài hàm khác để có thể phù hợp hơn, và cuối cùng thì mình đã tìm được hàm mà mình cho là phù hợp.

$\frac{1}{P}.\frac{dP}{dt} = \alpha.\left(1-\frac{\sqrt{P}}{\sqrt{cap}}\right)$

Về cơ bản thì nó vẫn thoả mãn yêu cầu đặt ra, và phép căn sẽ giúp giảm lại tốc độ đi xuống, tạo ra một đường cong phù hợp với dữ liệu.
Sau đó thì mình cũng giải và tìm ra hàm $P$ tương ứng

$P={\left(\frac{b}{e^{\frac{-b.t + C}{2}} - a}\right)}^2$

với $a=\frac{-\alpha}{\sqrt{cap}}, b=\alpha$
Sau đó, thay công thức vào đoạn code trên và thử lại xem sao.

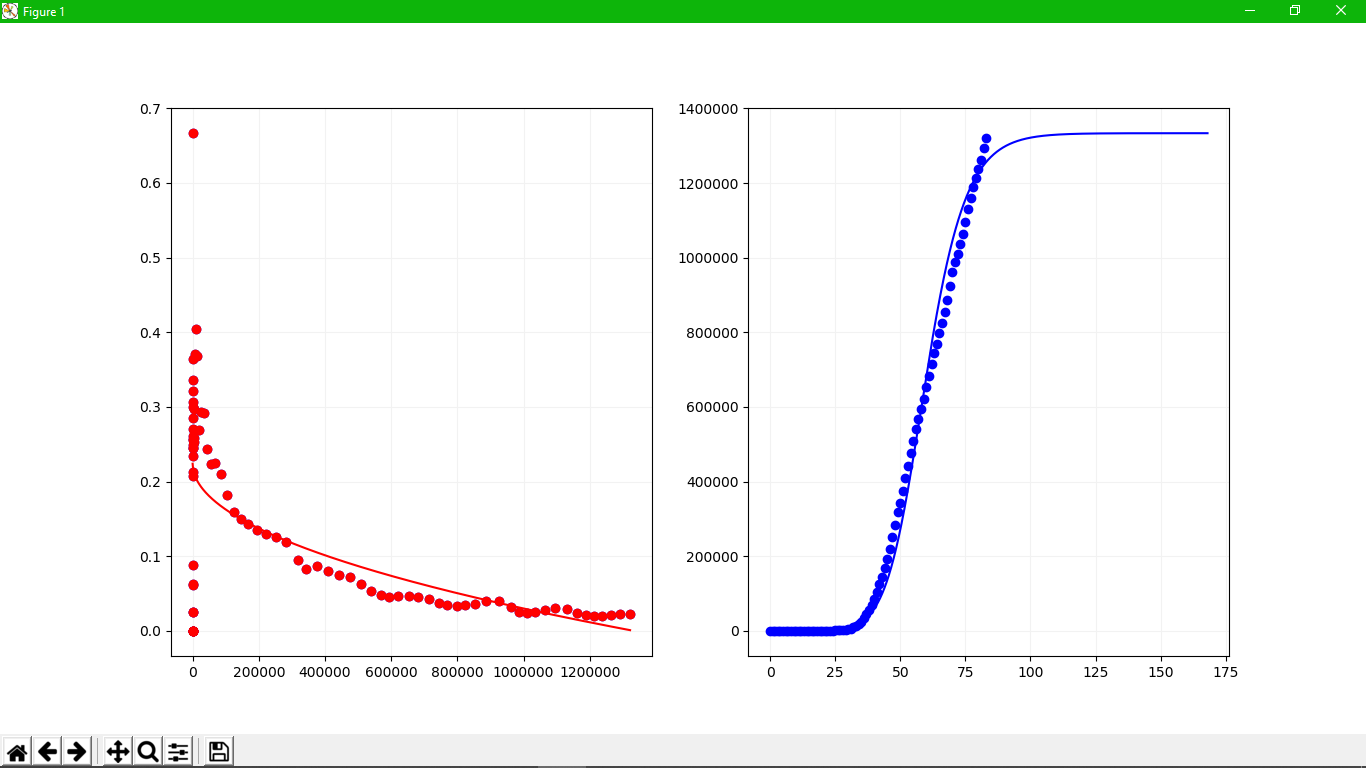
Trông có sự cải thiện hơn hẳn, nhưng rõ ràng là vẫn chưa đủ.

Nhiễu từ các giá trị đầu

Theo như đồ thị, các giá trị ban đầu tăng lên cực kỳ nhanh, sau đó mới từ từ giảm xuống theo 1 xu hướng, và vì quá trình hồi quy của chúng ta coi chúng có cùng vai trò với những giá trị sau, trong khi thực tế thì không. Các bạn hãy xem lại công thức để tính dãy tốc độ tăng tương đối

$\frac{1}{P}.\frac{dP}{dt}[t]=\frac{P[t+1]-P[t-1]}{2.P[t]}$

Với giai đoạn đầu của dịch, số lượng nhiễm quá ít làm cho sự thay đổi về số liệu phụ thuộc rất nhiều vào sự ngẫu nhiên, và vì $P$ nhỏ nên con số đó cũng dễ dàng bị đẩy lên rất cao khỏi xu hướng. Trong khi đó, những số liệu ban đầu này cũng có vai trò cực kì nhỏ trong hàm dự đoán, thế nên nó làm nhiễu hàm tốc độ tăng tương đối và hàm dự đoán cũng không chính xác.
Một cách để giải quyết đó là ta sẽ "lơ" đi một phần đầu của số liệu, và chỉ dùng phần sau để tìm hệ số. Phần code tìm hệ số được thay thành

while start < len(P) - 2:
  Xbar = np.array([P[start:]]).T
  Ybar = np.array([re_dP[start:]]).T

  reg = linear_model.LinearRegression()
  reg.fit(np.sqrt(Xbar), Ybar)
  print(reg.coef_, reg.intercept_)
  a = reg.coef_[0]
  b = reg.intercept_

  loss = 0
  for i in range(start, len(P)):
    _Y = re_dP[i]
    if _Y <= 1e-6:
      _Y = 0.001
    loss += np.abs(_Y - reg.predict(np.sqrt([[P[i]]]))) / _Y
  loss = loss / len(P)
  print('---LOSS--- ', loss)
  if loss <= args.loss or start == len(P) - 3:
    print(a, b)
    dX = np.linspace(0, P[-1], len(P) * 10)
    dY = a * np.sqrt(dX) + b
    # dY = a * dX + b
    ax[0].plot(P, re_dP, 'bo')
    ax[0].plot(P[start:], re_dP[start:], "ro")
    ax[0].plot(dX, dY, 'r-')
    ax[0].grid(axis='both', color='0.95')
    break
  start += 1

Nói đơn giản là nó sẽ tìm vị trí start phù hợp sao cho độ lỗi của re_dP[start:] là đủ nhỏ.

Phần chấm màu đỏ là vùng mình chọn để tìm hệ số
Đây là kết quả với args.loss = 0.1. Có vẻ như cuối cùng mình cũng tìm được một kết quả khá là mỹ mãn.

5. Nhận xét

Sử dụng kết quả này, mình dễ dàng đánh giá quá trình chống dịch của các nước trên thế giới. Những nước đã chạm tới phần nằm ngang của hàm dự đoán nghĩa là đỉnh dịch đã trôi qua, và dịch bệnh của nước đó đang trong quá trình suy thoái và kết thúc.
Ngoài ra, hãy thử tìm giới hạn của $P$ khi $t\rightarrow+\infty$

$lim_{t\rightarrow+\infty}P=lim_{t\rightarrow+\infty}{\left(\frac{b}{e^{\frac{-b.t + C}{2}} - a}\right)}^2={\left(\frac{b}{a}\right)}^2 = \left(\frac{\alpha}{\frac{-\alpha}{\sqrt{cap}}}\right)^2 = cap$

Điều này có nghĩa là hàm dự đoán mình tìm được là hoàn toàn chính xác, bởi theo định nghĩa thì quần thể về lâu dài sẽ tiến về $cap$ .
Ngoài ra, mình cũng biết được giá trị $\alpha=b$ chính là tốc độ tăng của quần thể, 2 giá trị này có thể được dùng để đánh giá hiệu quả chống dịch của các nước.

Lời kết

Chỉ với một vài bước tính nguyên hàm đơn giản, mình hoàn toàn có 1 cái nhìn tổng quan về hoạt động chống lại dịch bệnh COVID-19 đang hoành hành trên thế giới, và qua đó có thể dự đoán tình hình trong tương lai.
Mọi người có thể xem phần code hoàn chỉnh của mình tại đây