I. Tổng quan về kĩ thuật Two Pointers

Trong lập trình nói chung và lập trình thi đấu nói riêng, kĩ thuật hai con trỏ (two pointers) là một kĩ thuật rất hiệu quả để giải quyết các bài toán trên mảng hoặc chuỗi. Kĩ thuật này giúp tiết kiệm không gian lưu trữ, giảm thời gian chạy của giải thuật rất hiệu quả.

Vậy kĩ thuật hai con trỏ là gì? Đúng như tên gọi của nó, kĩ thuật này sử dụng hai con trỏ đồng thời để kiểm soát hai vị trí trên mảng hoặc chuỗi. Tuy nhiên khác với khái niệm con trỏ mà chúng ta thường biết (là một biến trỏ vào địa chỉ trong bộ nhớ máy tính của một đối tượng), con trỏ trong kĩ thuật này chỉ đơn giản là những biến kiểm soát vị trí trên mảng hoặc chuỗi, trong đó có một biến luôn luôn không vượt quá biến còn lại. Hình vẽ dưới đây là một minh họa:

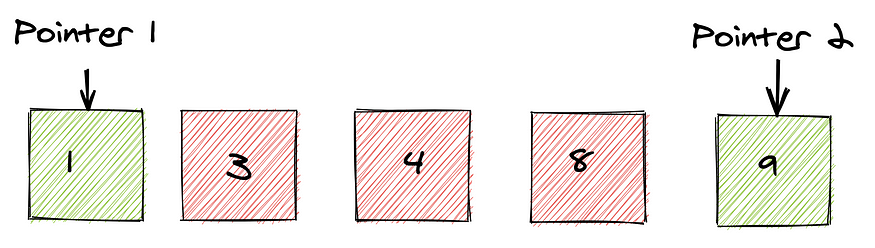
Trong rất nhiều bài toán trên mảng hoặc chuỗi, chúng ta sẽ phải quét qua các cặp giá trị, hoặc những đoạn liên tiếp trên dãy số. Nếu như sử dụng những vòng lặp lồng nhau, hoặc kết hợp các cấu trúc dữ liệu để kiểm soát các đoạn giá trị thì thời gian chạy của giải thuật sẽ không thể đảm bảo. Vậy giải pháp là gì? Chính là kĩ thuật two pointers - một giải pháp vừa tiết kiệm không gian lưu trữ, vừa giảm thời gian thực thi của giải thuật (thông thường xuống $O(n)$). Khi sử dụng two-pointers, thay vì chỉ truy cập được một phần tử của dãy, ta sẽ truy cập được đồng thời hai phần tử của dãy ở mỗi lần lặp, qua đó giảm số thao tác cần thực hiện đi rất nhiều.

Kĩ thuật này có thể chia làm ba dạng thường gặp:

• Slow And Fast: Một con trỏ chạy với tốc độ chậm, một con trỏ chạy với tốc độ nhanh.
• Left & Right Boundary: Hai con trỏ di chuyển ngược chiều nhau.
• Sliding Windows: Hai con trỏ di chuyển với cùng một tốc độ, về cùng một phía.

Sau đây chúng ta sẽ cùng phân tích ý tưởng của cả ba dạng toán thường gặp của kĩ thuật này thông qua những bài tập điển hình của chúng.

II. Dạng bài Slow And Fast

1. Giải thuật tổng quát

Trong dạng bài tập này, ta sẽ luôn luôn có một con trỏ đi phía trước với tốc độ chậm, và một con trỏ đi phía sau với tốc độ nhanh hơn. Thông thường, ở mỗi lần lặp, con trỏ phía sau sẽ luôn tăng lên, còn con trỏ phía trước thì chỉ tăng lên khi thỏa mãn một tập điều kiện nào đó.

<center>

</center>

Giải thuật tổng quát có thể viết mã giả như sau:

void slow_and_fast()
{
    pointer_1 = {chỉ số đầu};
    for (pointer_2 = {chỉ số đầu}; pointer_2 <= {chỉ số cuối}; ++pointer_2)
    {
        // Con trỏ thứ nhất chỉ tăng lên khi thỏa mãn một điều kiện nào đó.
        if ({pointer_1 thỏa mãn điều kiện})
            {Tăng pointer_1};

        {Xử lý logic sau khi tăng - giảm các con trỏ};
    }
}

Trong mã giả trên, các yếu tố có thể thay đổi tùy theo từng người lập trình và từng bài toán, nhưng ý tưởng thì vẫn không thay đổi. Ví dụ, vòng lặp for có thể thay bằng vòng lặp while, hay việc xử lý logic có thể đưa lên trước hoặc sau khi dịch chuyển con trò,...Ngoài ra, trong những bài toán phức tạp, có thể con trỏ phía sau cũng sẽ chỉ tăng lên khi đáp ứng được một tập điều kiện nào đó, vì vậy điều quan trọng ở đây là các bạn hiểu được ý tưởng thuật toán!

2. Bài toán ví dụ

Bài toán 1

Cho trước mảng số nguyên $A$ đã sắp xếp tăng dần.

Yêu cầu: Hãy loại bỏ các phần tử trùng lặp trong dãy và đưa ra độ dài của dãy mới?

Input:

• Dòng đầu tiên chứa số nguyên dương $n$ - kích thước dãy số.
• Dòng thứ hai chứa $n$ số nguyên $a_1, a_2, \dots, a_n$ phân tách nhau bởi dấu cách - các phần tử dãy số.

Ràng buộc:

• $1 \le n \le 10^5$.

Output:

• In ra kích thước của dãy số sau khi loại bỏ toàn bộ phần tử trùng lặp.

Sample Input:

Sample Output:

Ý tưởng

Bởi dãy số đã cho đã được sắp xếp tăng dần, nên các phần tử giống nhau chắc chắn sẽ đứng cạnh nhau.

Duy trì hai con trỏ $\text{slow}$ và $\text{fast}$ để kiểm soát các phần tử trên dãy. Con trỏ $\text{fast}$ sẽ duyệt qua tất cả các phần tử trên dãy, và con trỏ $\text{slow}$ sẽ chạy phía sau $\text{fast}$ và kiểm soát luôn kích thước của đoạn phần tử bằng với $a_\text{fast}$. Mỗi lần chạy qua, ta sẽ gán luôn $a_{\text{slow}} = a_{\text{fast}}$ để coi như "đặt cờ".

Kết quả cuối cùng chính là $\text{slow}$.

Độ phức tạp: $O(n)$.

Cài đặt

#include <bits/stdc++.h>

using namespace std;

main()
{
    int n;
    cin >> n;

    vector < int > a(n);
    for (int i = 0; i < n; ++i)
        cin >> a[i];

    int slow = 0;
    for (int fast = 1; fast < n; ++fast)
        // Nếu phần tử hiện tại không bị trùng lặp.
        if (num[fast] != num[slow])
        {
            // Dịch chuyển con trỏ slow lên 1 vị trí.
            // Copy vị trí hiện tại vào vị trí slow.
            ++slow;
            num[slow] = num[fast];
        }

    cout << slow + 1;

    return 0;
}

Bài toán 2

Cho dãy số $A$ gồm $n$ phần tử nguyên dương $a_1, a_2,..., a_n$. Độ hoàn hảo của một dãy con liên tiếp trong dãy $A$ được tính bằng trung bình cộng của dãy con đó.

Yêu cầu: Hãy tìm dãy con liên tiếp có độ hoàn hảo lớn nhất, với điều kiện dãy con đó có tổng không nhỏ hơn $K?$

Input:

• Dòng đầu tiên chứa hai số nguyên dương $n$ và $k$.
• Dòng thứ hai chứa $n$ số nguyên dương $a_1, a_2, \dots, a_n$ phân tách nhau bởi dấu cách.

Ràng buộc:

• $1≤n≤10^5$.
• $1≤k≤10^9$.
• $1≤a_i≤10^9; \forall i: 1 \le i \le n$.

Output:

• Chứa số nguyên duy nhất là độ hoàn hảo của dãy con có độ hoàn hảo lớn nhất.

Sample Input 1:

3 2
1 2 3

Sample Output 1:

3

Sample Input 2:

10 1
1 7 1 1 5 1 11 9 17 4

Sample Output 2:

17

Ý tưởng

Đặt $sum[i]$ là mảng tổng tiền tố của dãy $A$, chắc chắn mảng $sum$ sẽ tăng dần do các phần tử của dãy đều là số nguyên dương.

Với giới hạn $n$ nhỏ ta hoàn toàn có thể dùng hai vòng lặp để xét mọi dãy con có tổng không nhỏ hơn $k$ và lấy trung bình cộng lớn nhất của các dãy con đó. Tuy nhiên cách làm này chắc chắn không khả thi với giới hạn $n \le 10^5$ của bài toán này.

Để cải tiến thuật toán, ta sử dụng two pointers slow and fast như sau: Xét cặp vị trí $(i, j)$ đầu tiên thỏa mãn $sum[j] - sum[i] \ge k,$ đồng nghĩa với việc đoạn $[i + 1, j]$ có tổng lớn hơn hoặc bằng $k$. Lấy max độ hoàn hảo của đoạn đó.

Từ từ dịch con trỏ $i$ lên tới khi $sum[j] - sum[i] < k$. Mỗi lần dịch lên ta lại cập nhật độ hoàn hảo của đoạn $[i + 1, j],$ vì đoạn đang xét vẫn có tổng lớn hơn hoặc bằng $k$ cho tới tận khi nào $sum[j] - sum[i] < k$.

Sau khi dịch chuyển $i$ xong, xảy ra hai trường hợp:

• $i$ sau khi dịch chuyển vẫn giữ nguyên: Ta tăng $j$ lên $1$.
• $i$ sau khi dịch chuyển thay đổi so với ban đầu: Dịch chuyển $j$ lên tới khi $sum[j] - sum[i] \ge K$ trở lại.

Lưu ý do $sum[j] - sum[i]$ tương ứng với đoạn $[i + 1, j],$ nên $j$ bắt đầu từ $1, i$ bắt đầu từ $0$ tới $j - 1$.

Độ phức tạp: $O(n),$ do mỗi con trỏ chỉ đi qua cả dãy số đúng một lần.

Cài đặt

#include <bits/stdc++.h>
#define int long long

using namespace std;
const int maxn = 1e5 + 10;
int n, K, a[maxn], sum[maxn];

void enter()
{
    cin >> n >> K;

    for (int i = 1; i <= n; ++i)
    {
        cin >> a[i];
        sum[i] = sum[i - 1] + a[i];
    }
}

void solution()
{
    int i = 0, j = 1, max_perfect = 0;
	
    while (j <= n && sum[j] - sum[i] < K)
        ++j;

    while (i < j && j <= n)
    {
        int old_i = i;
        max_perfect = max(max_perfect, (sum[j] - sum[i]) / (j - i));

        while (i + 1 < j && sum[j] - sum[i + 1] >= K)
        {
            ++i;
            max_perfect = max(max_perfect, (sum[j] - sum[i]) / (j - i));
        }

        if (i == old_i)
            ++j;
        else
        {
            while (j <= n && sum[j] - sum[i] < K)
                ++j;
        }
    }

    cout << max_perfect << endl;
}

main()
{
    ios_base::sync_with_stdio(false);
    cin.tie(0); cout.tie(0);

    enter();
    solution();

    return 0;
}

III. Dạng Left & Right Boundary

1. Giải thuật tổng quát

Trong dạng bài này, ta sẽ sử dụng hai con trỏ, một con trỏ đi từ đầu dãy tiến lên, và một con trỏ đi từ cuối dãy lùi xuống (tất nhiên chỉ dịch chuyển khi thỏa mãn điều kiện nào đó). Chúng sẽ liên tục di chuyển cho tới khi gặp nhau ở giữa dãy số.

<center>

</center>

Dạng bài này có thể được biến đổi nâng cao thêm như sau:

• Hai con trỏ tạo thành một đoạn trong dãy số để xử lý logic.
• Hai con trỏ sẽ mang theo thông tin và cần xử lý logic ở mỗi lần lặp.

Lược đồ giải thuật có thể mô tả như sau:

void left_right_boundary(seq)
{
    left = 0, right = seq.size() - 1;
    while (left < right)
    {
        if ({left thỏa mãn điều kiện})	
            left += 1;
        if ({right thỏa mãn điều kiện})
            right -= 1;
		
        // Xử lý logic, có thể trước hoặc sau khi dịch chuyển hai con trỏ.
        {Xử lý logic};
    }
}

2. Bài toán ví dụ

Bài toán 1

Cho dãy số $A$ gồm $n$ phần tử $a_1, a_2, \dots, a_n$ đã được sắp xếp theo thứ tự tăng dần.

Yêu cầu: Đếm số cặp phần tử $(a_i, a_j)$ thỏa mãn $a_i + a_j = k$ với $k$ là số nguyên cho trước? Lưu ý, hai cặp số là hoán vị của nhau thì chỉ tính một lần.

Input:

• Dòng đầu tiên chứa hai số nguyên dương $n$ và $k$.
• Dòng thứ hai chứa $n$ số nguyên dương $a_1, a_2, \dots, a_n$ phân tách nhau bởi dấu cách.

Ràng buộc:

• $1 \le n \le 10^7$.
• $1 \le k \le 10^9$.
• $1 \le a_i \le 10^9; \forall i: 1 \le i \le n$.

Output:

• In ra số lượng cặp số tìm được.

Sample Input:

7 15
1 3 5 7 8 9 10

Sample Output:

2

Ý tưởng

Phương án hai vòng lặp cho bài toán này quá đơn giản nên tôi sẽ không nhắc đến nữa.

Một phương án khác mà các bạn học sinh thường nghĩ đến cho bài toán này sẽ là duyệt mọi $a_i$ và tìm kiếm nhị phân số lượng giá trị $a_j = k - a_i$ trong dãy số. Tuy nhiên, với giới hạn $n \le 10^7,$ thì giải thuật $O\big(n. \log(n)\big)$ vẫn sẽ bị quá thời gian chạy 1s. Ta cần giải thuật tốt hơn, đó chính là two - pointers.

Sử dụng con trỏ $\text{left}$ đặt ở đầu dãy số, và con trỏ $\text{right}$ đặt ở cuối dãy số. Do dãy số đã sắp xếp tăng dần, nên ở mỗi bước lặp, ta xử lý logic như sau:

• Nếu tồng $a_\text{left} + a_\text{right} < k$ thì tăng $\text{left}$ lên một đơn vị.
• Nếu tồng $a_\text{left} + a_\text{right} = k$ thì tăng kết quả lên một đơn vị.
• Nếu tồng $a_\text{left} + a_\text{right} > k$ thì giảm $\text{right}$ đi một đơn vị.

Quá trình lặp sẽ kết thúc khi $\text{left}$ và $\text{right}$ chạm vào nhau. Lúc này ta có được giải thuật với độ phức tạp chỉ là $O(n)$.

Cài đặt

#include <bits/stdc++.h>

using namespace std;

main()
{
    int n, k;
    cin >> n >> k;
	
    vector < long long > a(n + 1);
    for (int i = 1; i <= n; ++i)
        cin >> a[i];
	
    int res = 0;
    int left = 1, right = n;
    while (left < right)
    {
        if (a[left] + a[right] == k)
            ++res;
        else if (a[left] + a[right] < k)
            ++left; 
        else 
            --right;
    }
	
    cout << res;
}

Bài toán 2

Một hàng rào gồm $n$ thanh rào có độ cao lần lượt là $h_1, h_2, \dots, h_n;$ khoảng cách giữa các thanh rào với nhau bằng chính xác một đơn vị. Người ta muốn cải tạo hàng rào bằng cách chọn ra hai thanh rào bất kỳ, rồi căng một bức tranh lên đó. Bức tranh có diện tích càng lớn thì hàng rào sẽ càng trở nên đẹp mắt. Biết rằng, nếu căng một bức tranh lên hai thanh rào $(i, j)$ thì chiều cao và chiều dài của bức tranh đó sẽ lần lượt là: $\text{min}(h_i, h_j)$ và $j - i$.

<center>

</center>

Yêu cầu: Tìm ra diện tích lớn nhất có thể của bức tranh căng lên?

Input:

• Dòng đầu tiên chứa số nguyên dương $n$.
• Dòng thứ hai chứa $n$ số nguyên dương $h_1, h_2, \dots, h_n$ phân tách nhau bởi dấu cách.

Ràng buộc:

• $2 \le n \le 10^5$.
• $1 \le h_i \le 10^4; \forall i: 1 \le i \le n$.

Output:

• In ra diện tích lớn nhất có thể của bức tranh căng lên.

Sample Input:

9
1 8 6 2 5 4 8 3 7

Sample Output:

49

Ý tưởng

Ta sử dụng hai con trỏ để kiểm soát hai thanh rào ở mỗi bước lặp. Ban đầu coi $\text{left} = 1, \text{right} = n$ và diện tích lớn nhất mặc định sẽ là giữa hai thanh rào thứ $1$ và thứ $n$.

Ở mỗi lần lặp, ta sẽ lựa chọn xem chiều cao của bức tranh tạo ra sẽ là $\text{left}$ hay $\text{right}$ (bên nào thấp hơn sẽ được chọn). Sau đó, dịch chuyển con trỏ ở bên tương ứng cho tới khi thu được một thanh rào có chiều cao lớn hơn chiều cao đã chọn, để loại bỏ trước những phương án không tốt hơn kết quả hiện tại.

Kết thúc mỗi bước lặp ta cập nhật diện tích bức tranh lớn nhất vào một biến $\text{max\_area}$.

Độ phức tạp: $O(n)$.

Cài đặt

#include <bits/stdc++.h>

using namespace std;

void solution(vector < int > &height)
{
    int left = 0, right = height.size() - 1;
    int max_area = (right - left) * min(height[left], height[right]);

    while (left < right)
    {
        // Chiều cao nhỏ hơn sẽ quyết định chiều cao bức tranh.
        if (height[left] <= height[right])
        {
            last_height = height[left];

            while (height[left] <= last_height && left < right)
                ++left;
        }
        else 
        {
            last_height = height[right];
            while (height[right] <= last_height && left < right)
                --right;
        }

        if (left >= right)
            return max_area;

        max_area = max(max_area, (right - left) * min(height[right], height[left]));
    }

    return max_area;
}

main()
{
    int n;
    cin >> n;

    vector < int > height(n);
    for (int i = 0; i < n; ++i)
        cin >> height[i];

    cout << solution(height);

    return 0;
}

IV. Dạng Sliding Window

1. Giải thuật tổng quát

Kĩ thuật Sliding Windown là một kĩ thuật khá thú vị, nó có thể được áp dụng vào những bài toán điển hình. Ý tưởng của kĩ thuật này khá giống với kĩ thuật slow & fast, khi chúng ta sử dụng hai con trỏ liên tục tịnh tiến về phía sau, tuy nhiên điểm đáng lưu ý là kết quả của bài toán sẽ liên tục được cập nhật dựa vào đoạn con được kiểm soát bởi hai con trỏ đó.

Hãy tưởng tượng rằng ta có một chiếc xe bus với độ dài cố định, $\text{start}$ và $\text{end}$ lần lượt là điểm đầu và điểm cuối của xe. "Chiếc xe" này sẽ liên tục di chuyển trên dãy số cho tới khi hết dãy. Trong quá trình "trượt" trên dãy số, ta sẽ xử lý logic và cập nhật kết quả cần thiết của bài toán.

<center>

</center>

Mô hình thuật toán có thể mô tả như sau:

void sliding_window(seq)
{
    // Xác định kích thước của đoạn trượt: window_size
    start = 0, end = start + window_size - 1;

    while (end < seq.size())
    {
        {Tính toán kết quả của window hiện tại};
        {Dịch chuyển window ra phía sau};
        {Cập nhật kết quả tốt nhất};
    }
}

Các bước cần làm trong kĩ thuật Sliding Window có thể tóm tắt như sau:

• Xác định kích thước của "window" - tức là khoảng cách giữa hai con trỏ. Kích thước này có thể là cố định hoặc không cố định, tùy vào bài toán.
• Tính toán kết quả cho "window" thứ nhất (tức là tính từ vị trí $\text{start}$ của đoạn hiện tại).
• Sử dụng vòng lặp để tịnh tiến "window" ra phía sau một đơn vị, rồi tiếp tục tính toán kết quả trên "window" mới.

Kĩ thuật Sliding Window rất hữu ích trong các bài toán liên quan tới kết quả lớn nhất/nhỏ nhất trên các đoạn cố định của dãy số hoặc chuỗi kí tự. Sau đây chúng ta sẽ cùng xem xét một số ví dụ tiêu biểu của kĩ thuật này.

2. Bài toán ví dụ

Bài toán 1

Cho trước dãy số $A$ gồm $n$ phần tử $a_1, a_2, \dots, a_n$ và một số nguyên dương $k$.

Yêu cầu: Hãy xác định đoạn con có kích thước bằng $k$ có tổng lớn nhất?

Input:

• Dòng đầu tiên chứa hai số nguyên dương $n$ và $k$.
• Dòng thứ hai chứa $n$ số nguyên $a_1, a_2, \dots, a_n$ phân tách bởi dấu cách.

Ràng buộc:

• $1 \le k \le n \le 10^5$.
• $|a_i| \le 10^9; \forall i: 1 \le i \le n$.

Output:

• In ra tổng của đoạn con tìm được.

Sample Input:

9 4
1 4 2 10 2 3 1 0 20

Sample Output:

24

Ý tưởng

Dễ thấy, do các đoạn con ta cần xét có kích thước cố định bằng $k$ nên kích thước của window sẽ chính bằng $k$.

Nếu như xét mọi đoạn con độ dài $k$ bằng hai vòng lặp thì chắc chắn sẽ bị quá thời gian, do $n \le 10^5$.

Ta xét liên tục các đoạn con độ dài $k$ bằng cách sử dụng sliding window như sau: Gọi $\text{window\_sum}$ là tổng của đoạn con đang xét. Nhận thấy, mỗi khi tịnh tiến window ra phía sau một đơn vị, giả sử nó kết thúc tại vị trí $i$ thì tổng đoạn con sẽ thay đổi một lượng là:

$$\text{window\_sum} = \text{window\_sum} + a_i - a_{i - k}$$

Vì thế, ta chỉ cần sử dụng một vòng lặp để liên tục cập nhật tổng đoạn con lớn nhất.

Độ phức tạp: $O(n)$.

Cài đặt

#include <bits/stdc++.h>
#define int long long

using namespace std;

main()
{
    int n, k;
    cin >> n >> k;

    vector < int > a(n + 1);
    for (int i = 1; i <= n; ++i)
        cin >> a[i];

    int res = accumulate(a.begin() + 1, a.begin() + k + 1);
    int window_sum = res;
    for (int i = k + 1; i <= n; ++i)
    {
        window_sum += (a[i] - a[i - k]);
        res = max(res, window_sum);
    }

    cout << res;
}

Bài toán 2

Cho trước một dãy số $A$ gồm $n$ số nguyên là các bit $0$ và $1$ cùng với một số nguyên dương $k$.

Yêu cầu: Hãy tìm một tập gồm nhiều nhất các đoạn con của dãy $A$ sao cho kích thước của các đoạn con đó đều đôi một khác nhau, và tổng của các đoạn con đều bằng $k?$

Input:

• Dòng đầu tiên chứa hai số nguyên dương $n$ và $k$.
• Dòng thứ hai chứa một dãy số gồm $n$ số $0$ hoặc $1$ phân tách nhau bởi dấu cách.

Ràng buộc:

• $1 \le k \le n \le 10^5$.

Output:

• In ra kích thước lớn nhất của tập hợp các đoạn con tìm được. Nếu không tồn tại thì in ra $0$.

Sample Input:

4 2
0 1 1 0

Sample Output:

3

Giải thích:

Tập các đoạn con tìm được là: $\big\{\{0, 1, 1, 0\}; \{0, 1, 1\}; \{1, 1\}\big\}$.

Ý tưởng

Nhận thấy, tổng của một đoạn con chính là số lượng số $1$ trong đoạn con đó. Ta sử dụng kĩ thuật sliding window như sau:

• Duy trì một biến $count$ để đếm số lượng số $1$ trong window hiện tại.
• Nếu $count < k$ thì tăng kích thước window lên, còn ngược lại thì giảm kích thước của windown xuống.
• Với các windown có $count = k,$ ta đẩy kích thước của window đó vào một set để lưu trữ các giá trị khác nhau.
• Cuối cùng, kích thước của set chính là kết quả bài toán.

Độ phức tạp: $O(n)$.

Cài đặt

#include <bits/stdc++.h>

using namespace std;

int maximum_subset(int n, vector < int > &a, int k)
{
    unordered_set < int > s;

    // Vị trí bắt đầu và tổng của window hiện tại.
    int ptr = 1;
    int window_sum = 0;
    for (int i = 1; i <= n; ++i)
    {
        // Cập nhật tổng đoạn con kết thúc tại a[i].
        window_sum += a[i]; 

        // Nếu tổng window hiện tại < k thì tiếp tục tăng kích thước window.
        if (window_sum < k)
            continue;
        
        // Nếu tổng window hiện tại > k thì dịch vị trí xuất phát của window lên.
        if (cur_sum > k)
        {
            while (cur_sum > k)
                cur_sum -= a[ptr++];
        }

        // Nếu tổng window hiện tại = k thì lấy tất cả các đoạn con như vậy đưa vào set.
        if (cur_sum == k)
        {
            s.insert(i - ptr + 1);

            int j = ptr;
            while (a[j] == 0)
            {
                s.insert(i - t);
                ++t;
            }
        }
    }

    return s.size();
}

main()
{
    int n, k;
    cin >> n >> k;

    vector < int > a(n + 1);
    for (int i = 1; i <= n; ++i)
        cin >> a[i];

    cout << maximum_subset(n, a, k);

    return 0;
}

V. Tài liệu tham khảo

• https://www.pluralsight.com/guides/algorithm-templates:-two-pointers-part-2
• https://www.baeldung.com/java-two-pointer-technique
• https://www.pluralsight.com/guides/algorithm-templates:-two-pointers-part-3