Trie

In computer science, use of string and handling them for different purpose is very inportant thing. There are some data structure for work with string in programming language. TRIE is one of them. Today we will discuss about it.

Trie

Trie is an ordered tree data structure used to store a dynamic set or associative array where the keys are usually strings. It is also known as radix tree or prefix tree in the computer world. The word "trie" comes from the word "retrieval". Unlike a binary search tree, no node in the tree stores the key associated with that node; instead, its position in the tree defines the key with which it is associated. All the descendants of a node have a common prefix of the string associated with that node, and the root is associated with the empty string. Keys tend to be associated with leaves, though some inner nodes may correspond to keys of interest. Hence, keys are not necessarily associated with every node.

Example

Suppose we have a dictionary with the following words.

Algo, Algea, Also, Tom, to

Now we need to find a way to save them in such a manner that we can retrieve them easily. One of the way is to save them in sorted order. So after that binary search will do rest. and another way is using trie.

Algorithm

Now we will build the Trie for the above example. At first there is no other in our structure except root. Now we will add algo. We will add a edge from root node and give the edge name 'a'. From the newly created node, we add an 'l' edge to new node. After adding 'g' and 'o' edge the trie will look like this -

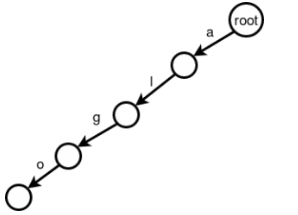
Now We will add the second word, which is Algea. So first we need to add 'a' edge from root. But there is already an 'a' edge from root. if you go further you will also find edge from 'a' to 'l' and 'l' to 'g'. We only need to add edge 'e' and 'a'. The same procedure follows for Also. We only need to add 's' and 'o' edge. So now our trie looks like -

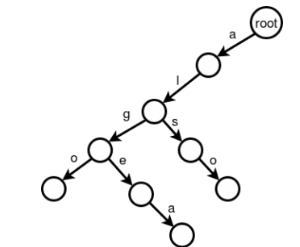
next we will add Tom in the try. As there is no 't' edge so we need to do it from scratch. Now To is a complete prefix of Tom so we dont need to add anything. we only need to color the last node of each word as gray to understand the last of each word. So our final trie get the following structure -

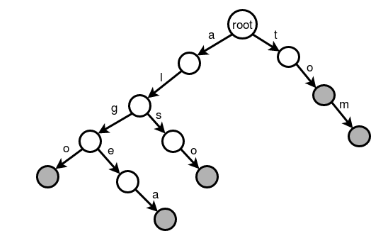
So now what is the importance of storing words like this. Because it is easy to find any word from this structure. Suppose if you want to find "anh" in this structure. First you need to check for 'a' edge from root. Yes, we have this in trie. Next we need to find 'n' edge from the current node. But we dont have this. So "anh is not in our dictionary. Generally we need to do number of letter operations to find a word in Trie.

Implemantation

The ruby implementation is given below -

class Node
  attr_reader :data, :edges
  attr_accessor :color
  def initialize(data)
    @data = data
    @edges = []
    @color = false
  end

  def insert(char)
    return get(char) if have?(char)
    child = Node.new(char)
    @edges << child
    child
  end

  def have?(char)
    @edges.each do |c|
      return true if c.data == char
    end
    false
  end

  def get(char)
    @edges.each do |child|
      return child if child.data == char
    end
    false
  end
end

class Trie
  attr_reader :root
  def initialize
    @root = Node.new(nil)
  end

  def insert(word)
    node = @root
    word.size.times do |i|
      child = node.insert(word[i])
      node = child
    end
    node.term = true
  end

  def have?(word)
    node = @root
    word.size.times do |i|
      return false unless node.have?(word[i])
      node = node.get(word[i])
    end
    node.color
  end
end

Complexity

Searching complexity of trie is O(length of search word). Inserting complexity is also the same. Memory required for storing is dependent on number of word and how much prefix is common.

Hope this helps. Thank you

Example taken: http://www.shafaetsplanet.com/?p=1679