Trao đổi khóa Diffie-Hellman

Mô tả bài toán

Đối với các hệ thống giao tiếp giữa 2 endpoint thông qua một server trung gian. (như các hệ thống HelpDesk (remote desktop), chat client -server ...)

Ta có thể áp dụng cơ chế như SSL\TLS để xác thực hai chiều, mã hóa kênh truyền, nhưng phương pháp này chỉ đảm bảo an toàn giao tiếp giữa Client - Server, đâu đó vẫn còn tiềm tàng nguy cơ bị tấn công khi kẻ gian kiểm soát được đường truyền mạng giữa server và client hoặc kiểm soát được chính server, yêu cầu đặt ra cần một phương pháp trao đổi khóa mã hóa chung giữa 2 đầu endpoint (client) và đảm bảo rằng key mã hóa chung này chỉ có 2 client biết với nhau, và hoàn toàn bí mật đối với server hoặc kẻ gian nằm giữa kênh truyền. Trong bài viết này, sẽ tập trung vào việc mô tả phương pháp trao đổi khóa Diffie - Hellman để giải quyết bài toán trên.

Mô tả thuật toán

Đây là giao thức giúp cho 2 máy tính trao đổi thông tin với nhau một cách bảo mật bằng cách tạo ra shared private key.

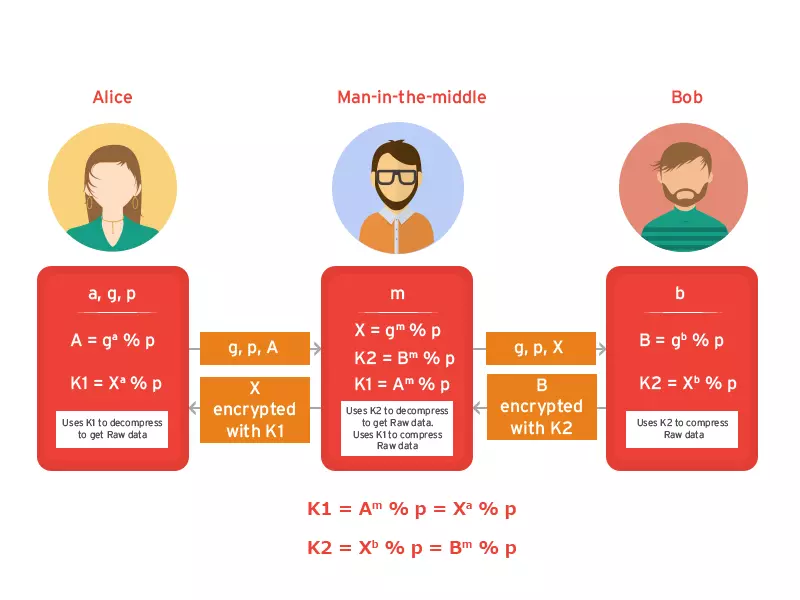
Giả sử 2 máy tính là A và B. Đầu tiên 2 máy tạo ra 2 số nguyên tố p và g, khi p lớn (thường lớn hơn 512 bits) và g là primitive root modulo của số p. p và g không cần giữ bí mật với các users khác. Khi đó, A và B tự chọn cho mình một số đủ lớn ngẫu nhiên làm private key, giả sử A chọn số a và B chọn số b.

Bây giờ A tính A = ga (mod p) và gửi cho B, B tính số gb (mod p) và gửi ngược lại cho A. Hai mã này là shared key. A và B sẽ thực hiện phép tính dựa và key nhận được.

A tính: K = Ba (mod p) = (gb)a (mod p) và B: K = Ab (mod p) = (ga)b (mod p)

Bây giờ 2 máy có thể sử dụng shared key K của mình để trao đổi dữ liệu mà không cần phải sợ dữ liệu bị nghe lén. Hai máy A và B có thể tìm được a từ công thức A = ga (mod p) và b từ B = gb (mod p). Có thể tham khảo thêm ở hình minh họa ở trên.

Trình tự xử lý dưới client sử dụng OpenSSL

#include <openssl/dh.h>

DH *privkey;
int codes;
int secret_size;

/* Sinh khóa bí mật phía client, khóa có kích thước 2048 bit */
if(NULL == (privkey = DH_new()))
{
    handleErrors();
}
if(1 != DH_generate_parameters_ex(privkey, 2048, DH_GENERATOR_2, NULL))
{
    handleErrors();
}

//Kiểm tra tính hợp lệ của khóa bí mật đã sinh
if(1 != DH_check(privkey, &codes)) handleErrors();
if(codes != 0)
{
    printf("DH_check failed\n");
    abort();
}

/* Sinh cặp khóa bí mật và công khai dựa trên khóa bí mật đã tính được ở trên */
if(1 != DH_generate_key(privkey))
{
    handleErrors();
}

/* Gửi khóa công khai cho đối tác*/
/* Bước này sẽ phụ thuộc vào mục đích sử dụng của ứng dụng*/

/* Nhận khóa công khai của đối tác*/
/* Giả sử khóa công khai của đối tác nhận được có giá trị là 01234567890123456789012345678901234567890123456789*/
BIGNUM *pubkey = NULL;
if(0 == (BN_dec2bn(&pubkey, "01234567890123456789012345678901234567890123456789")))
{
    handleErrors();
}

/* Tính toán giá trị khóa bí mật dùng chung của hai bên */
unsigned char *secret;
if(NULL == (secret = OPENSSL_malloc(sizeof(unsigned char) * (DH_size(privkey)))))
{
    handleErrors();
}

if(0 > (secret_size = DH_compute_key(secret, pubkey, privkey)))
{
    handleErrors();
}
/* Sử dụng khóa bí mật dùng chung đã tính được ở trên để má hóa dữ liệu trao đổi giữa hai bên */

printf("The shared secret is:\n");
BIO_dump_fp(stdout, secret, secret_size);

/* Giải phóng context */
OPENSSL_free(secret);
BN_free(pubkey);
DH_free(privkey);

Chương trình mô tả thuật toán

Để mô tả trình tự các bước xử ly theo thuật toán trên, em đã viết một chương trình chat server - client (TCP Socket)

Chương trình hoạt động như sau:

• Server (sử dụng python): đóng vai trò trung gian kết nối và trao đổi dữ liệu giữa các client
• Client (sử dụng iOS Swift):
  • Người dùng trước khi chat với đối tác sẽ sinh một cặp khóa công khai và bí mật, và trao đổi khóa công khai của mình với đối tác của mình
  • Sau khi đã trao đổi khóa công khai thành công => tính giá trị khóa bí mật dùng chung theo thuật toán mô tả dùng chung (Các bước tính toán này sử dụng thư viện OpenSSL)
  • Sau đó mọi dữ liệu chat giữa hai bên sẽ được mã hóa AES với khóa bí mật dùng chung đã được tính toán ở trên.

Code chương trình mọi người có thể tải tại địa chỉ: https://github.com/TuInh/Report-12.git

Nguồn: https://en.wikipedia.org/wiki/Diffie–Hellman_key_exchange