Mạng nơ-ron được lấy cảm hứng từ cấu trúc và cơ chế truyền nhận thông tin từ bộ não người. Mạng nơ-ron cho phép mô hình học được những dữ liệu đầu vào thông qua rất nhiều các lớp (layers) chứa các nút khác nhau (giống tế bào não người) và chúng được kết nối với nhau như những dây thần kinh vậy. Điều này giúp chúng xử lý và truyền thông tin giữa các nơ-ron trong mạng lưới.

1. Hàm kích hoạt trong DL là gì?

Hàm kích hoạt trong DL là hàm phi tuyến tính, cho phép mô hình học được những mẫu phức tạp và thể hiện được mối liên hệ dữ liệu giữa chúng.

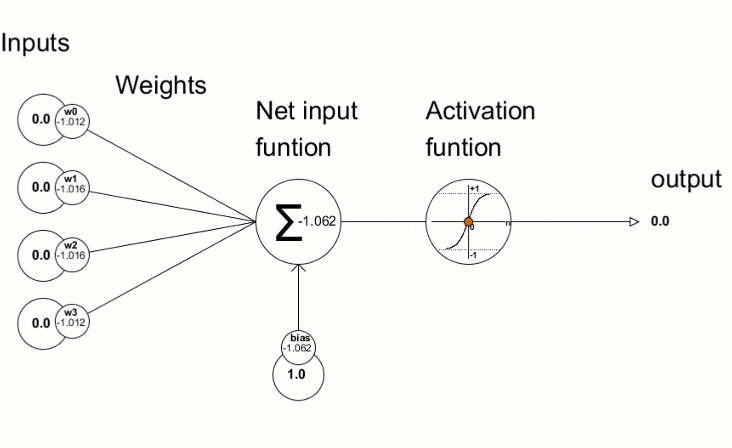
2. Tại sao chúng ta lại cần hàm kích hoạt là hàm phi tuyến tính

Chuyện gì sẽ xảy ra khi chúng ta sử dụng hàm kích hoạt là hàm tuyến tính trong mạng nơ-ron?

Để mô tả đơn giản cho điều này, tôi gọi đầu vào của một lớp ẩn (hidden layer) là X, đầu ra của lớp ẩn này là Z thông qua trọng số (weight) là W và bias là b.

$$Z = W^{T}*X + b$$

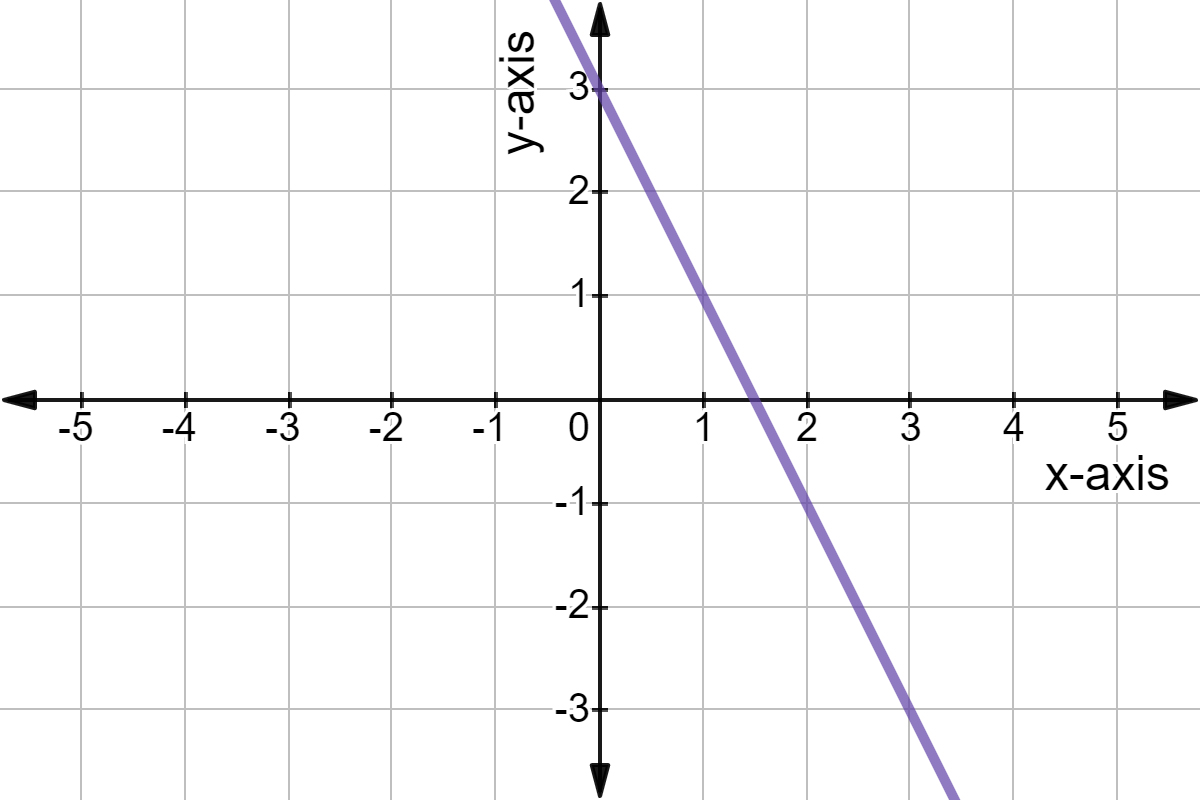
Có hai vấn đề khi sử dụng hàm tuyến tính:

Backpropagation lúc này là vô dụng (tức bạn không thể cập nhật được trọng số qua quá trình huấn luyện): Để huấn luyện mô hình chúng ta cần tính gradient nhưng đạo hàm của hàm tuyến tính lại là hằng số, không có mối liên hệ với dữ liệu đầu vào X (bạn có thể thử đạo hàm số tuyến tính và một hàm phi tuyến tính như sigmod là sẽ thấy). Vì vậy, mà mô hình chả thể cải thiện được trọng số nào để mô hình có thể tốt lên.

Nếu bạn có suy nghĩ làm cho mô hình sâu hơn trong mạng để học thì bỏ đi vì nó chả khác nào là 1 lớp cả: Đơn giản là tổ hợp của các hàm tuyến tính là một hàm tuyến tính mà thôi.

Đó là lý do vì sao mà chúng ta phải sử dụng hàm phi tuyến tính làm hàm kích hoạt trông mô hình.

3. Hàm kích hoạt phi tuyến tính

Hàm phi tuyến tinh cho phép mô hình ánh xạ phức tạp giữa dữ liệu đầu vào với đầu ra của các lớp trong mạng, mô hình hóa được dữ liệu phức tạp. Đặc biệt, chúng giải quyết được các vấn đề mà hàm tuyến tính gặp phải.

4. Một số các hàm phi tuyến tính

4.1. Hàm sigmoid

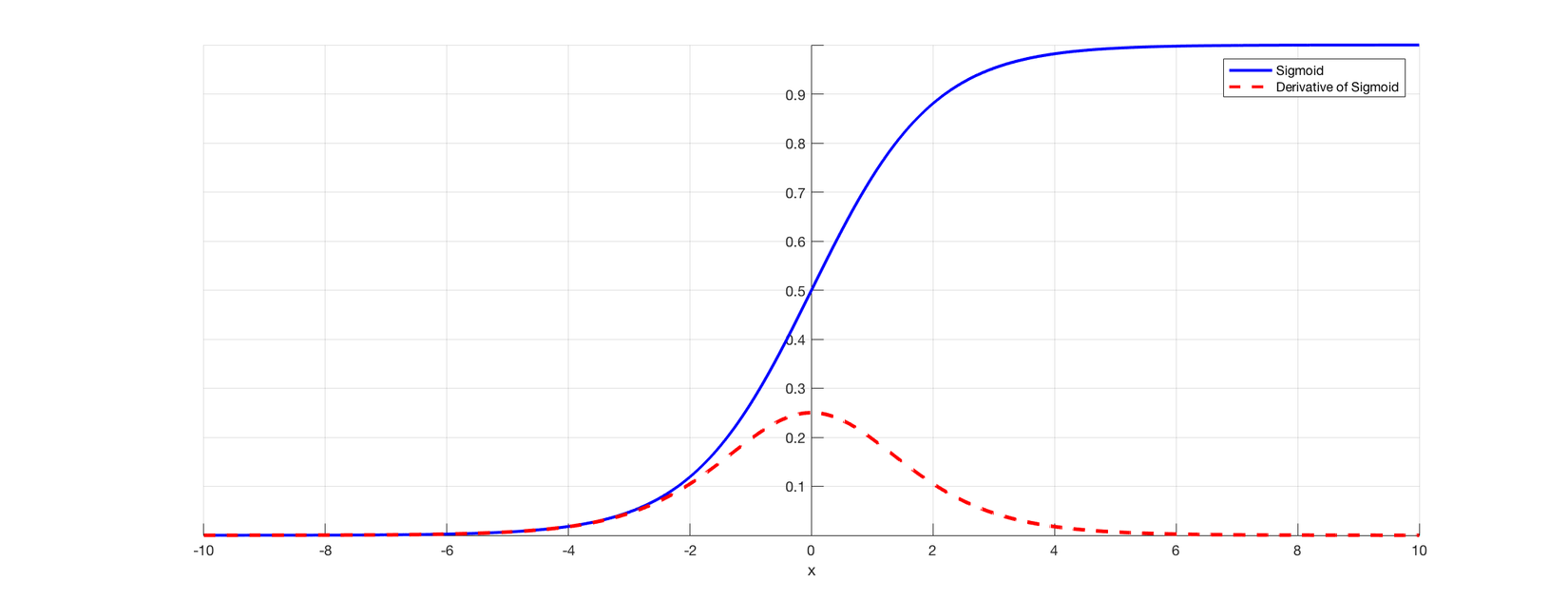
Hàm sigmoid (Logistic)

$$y = f(x) = \frac{1}{1 + e^{-x}}$$

Khi đó đạo hàm của hàm f(x): $f'(x) = f(x)(1 - f(x))$

** Ưu điểm:

• Khoảng giá trị output sẽ nằm trong khoảng 0 và 1, có thể dùng là chuẩn hóa giá trị output của mạng nơ-ron.
• Các giá trị hoặc $x \ge 2$ và $x \le -2$ và các giá trị output sẽ tiến tiệm cận tới 1 hoặc 0. Khi đó việc dự đoán sẽ trở nên dễ rõ ràng hơn.

** Nhược điểm:

• Khi x có giá trị rất lớn thì giá trị của y của hàm sigmoid hầu như không thay đổi, gây ra hiện tượng vanishing gradient (tức không có sự cập nhật trọng số qua các lần backpropagation) khiến cho mô hình không học được gì hoặc hoặc được rất ít (Dựa vào đạo hàm của hàm số trên là chúng ta sẽ thấy hiện tượng đó).
• Nó đòi hỏi nhiều tính toán hơn vì nó yêu cầu tính toán số mũ, điều này làm cho sự hội tụ của mạng chậm hơn.
• Do hàm này không lấy số 0 làm trung tâm nên gradient của các trọng số được kết nối với cùng một nơ-rơn là dương hoặc âm dẫn tới những lần cập nhật trọng số, chúng di chuyển theo một hướng tích cực hoặc tiêu cực. Điều này làm ảnh hưởng đến việc hội tụ trong tối ưu hóa.

4.2. Hàm tanh

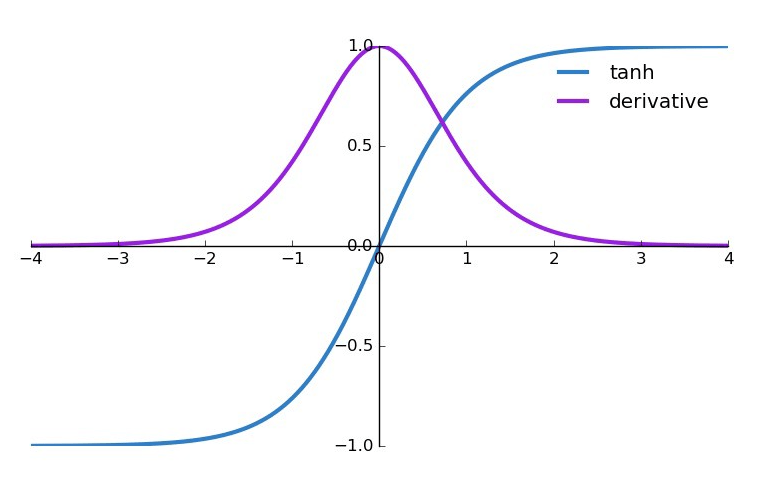
Hàm tanh (Hyperbolic tangent)

$$y = \frac{e^x - e^{-x}}{e^x + e^{-x}}$$

Khi đó đạo hàm của hàm f(x): $f'(x) = 1 - f(x)^2$

** Ưu điểm:

• Khoảng giá trị output sẽ nằm trong khoảng -1 và 1, dùng làm chuẩn hóa đầu ra của mạng nơ-ron.
• Không giống như sigmoid, tanh lấy 0 làm trung tâm để việc tối ưu hóa trở nên đơn giản hơn.

** Nhược điểm

• Hàm này cũng đòi hỏi nhiều tính toán do vẫn tính toán hàm số mũ.
• Khi giá trị đầu vào quá lớn hoặc quá nhỏ sẽ bị vanishing gradient giống sigmoid.

4.3. Hàm ReLu

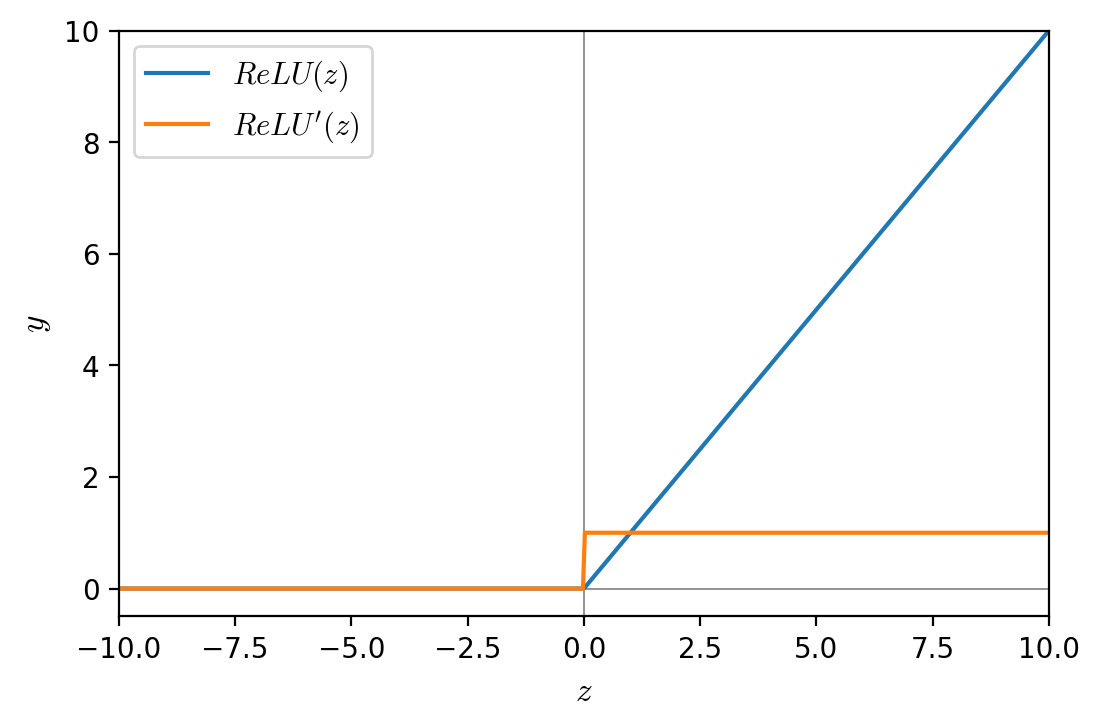
Hàm ReLu (Rectified Linear Unit)

$$f(x) = \begin{cases} 0 && x \lt 0 \\ x && x \ge 0 \end{cases}$$

Khi đó đạo hàm của hàm f(x):

$$f(x)' = \begin{cases} 0 && x \lt 0 \\ 1 && x \ge 0 \end{cases}$$

** Ưu điểm

• Dễ dàng tính toán để mạng nơ-ron hội tụ nhanh. ** Nhược điểm
• Hiện tượng vanishing gradient xảy ra khi có đầu vào là giá trị âm hoặc bằng 0 do graident các giá trị đó đều bằng 0.

4.4. Hàm Leaky ReLu

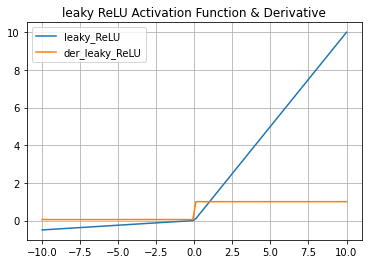
Hàm Leaky ReLu:

$$f(x) = \begin{cases} \alpha x && x \lt 0 \\ x && x \ge 0 \end{cases}$$

Khi đó đạo hàm của hàm f(x):

$$f(x)' = \begin{cases} \alpha && x \lt 0 \\ 1 && x \ge 0 \end{cases}$$

Chú ý rằng việc gọi tên hàm Leaky ReLu thì chúng ta đã hiểu là giá trị $\alpha = 0.01$ rồi. Còn nếu nó khác 0.01 thì nó sẽ gọi là Randomized ReLu.

** Ưu điểm:

• Dễ dàng tính toán đề mạng nơ-ron hội tụ nhanh
• Không xảy ra hiện tượng vanishing gradient khi các giá đầu vào là âm (do lúc này hàm đã có độ dốc nhỏ).

** Nhược điểm: Hiện tại mình chưa tìm ra nhược điểm của hàm này.

4.5. Hàm softmax

Tiện đây, mình đề cập một hàm cũng hay được sử dụng cho các bài toán phân loại ảnh đa lớp, đó là hàm softmax. Hàm này có vai trò đặc biệt khi mà nó vừa là hàm kích hoạt vừa là hàm phân phối xác xuất. Thường thì hàm này sẽ ở lớp đầu ra của mô hình.

Có một sự khác biệt giữa hàm softmax và các hàm kích hoạt phi tuyến tính trên là hàm softmã tác động lên toàn bộ thành phần của vector trong khi những hàm khác thì chỉ tác động đến từng thành phần của vecto thôi.

Hàm softmax:

$$\hat{y_i} = f(z_i) = \frac{e^{z_i}}{\sum_{j=1}^C e^{z_j}}, \forall i = 1, 2, ... C$$

Trong công thức trên C đại diện cho các lớp cần phân loại. $y_i$ đại diện cho xác xuất của lớp đầu ra dự đoán của mô hình. $z_i = w_i^Tx$ là kết quả khi qua node trong mạng nơ-ron trước khi qua hàm softmax.

Chú ý rằng: $\sum_{i = 1}^C y_i = 1$ do tổng xác xuất của mỗi lớp cần phân loại là bằng 1.

Nếu để ý kỹ bạn sẽ thấy khi $C = 2$ thì hàm softmax sẽ trở về hàm sigmoid. Mình sẽ biến đổi một chút để các bạn thấy

$$\hat{y_1} = \frac{exp(w_1^Tx)}{exp(w_1^Tx) + exp(w_2^Tx)} = \frac{1}{1 + exp((w_2 - w_1)^Tx)}$$

• Một câu hỏi đặt ra là tại sao chúng ta lại không quan tâm đến đạo hàm của hàm softmax trong các bài toán phân loại ảnh đa lớp (rõ ràng quá trình backpropagation cần có sự cập nhật trọng số và bias thì cần quan tâm đến đạo hàm giống như những hàm kích hoạt trên) ?

Để giải quyết câu hỏi trên, chúng ta cần phải xem đến vẻ đẹp của biến đổi toán học trong việc tối ưu hàm mất mát. Thường hàm mất mát trong các bài toán phân loại sử dụng Cross Entropy.

Hàm Cross Entropy trong bài toán phân loại đa lớp: $L = - \sum_{i = 1}^C y_ilog(y_i)$. Chú ý ký hiệu $log(y_i)$ chính là logarith cơ số e ở Việt Nam (hay ký hiệu là $ln(y_i)$) Do tôn trọng công thức của tác giả nên mình vẫn giữ nguyên.

Xét trên một điểm dữ liệu đầu vào là x và mạng nơ-ron chỉ có một lớp để đơn giản hóa biến đổi toán học. Xét trên một tập dữ liệu thì tương tự.

$$L = - \sum_{i =1}^C y_ilog(\frac{exp(w_i^Tx)}{\sum_{j = 1}^C exp(w_j^Tx)}) = - \sum_{i =1}^C y_iw_i^Tx + \sum_{i =1}^C y_ilog(\sum_{j = 1}^C exp(w_j^Tx))$$

Do $\sum_{i = 1}^C y_i = 1$ nên $L = - \sum_{i =1}^C y_iw_i^Tx + log(\sum_{j = 1}^C exp(w_j^Tx))$

Tính gradient cho $w_i$:

$$\frac{\delta L}{\delta w_i} = -y_ix + \frac{exp(w_i^Tx)}{\sum_{j = 1}^C exp(w_j^Tx)}x = - (y_i - \hat{y_i})x$$

Chú ý mình tính đạo hàm riêng từng phân $log(\sum_{j = 1}^C exp(w_j^Tx)$ theo $w_j$ rồi mình tổng lại thành đạo hàm theo $w_i$ nên mới có kết quả như trên.

Khi đó $\frac{\delta L}{\delta w} = - (y - \hat{y})x$ dẫn tới cập nhật ma trận trọng số $W = W + \gamma \frac{\delta L}{\delta w}$

Nếu nơ-ron có nhiều lớp thì việc tính toán để cập nhật các trọng số của lớp trước đó thì vẫn liên quan đến việc tính đạo hàm của hàm kích hoạt trước đó.

• Một câu hỏi nữa là, làm sao bạn biết rằng điểm dữ liệu x được dự đoán sẽ rơi vào lớp nào chứ? Các lớp phân tách nhau dựa vào gì?

Dựa vào hàm softmax chúng ta có thể thấy x rời vào lớp i nếu $y_i \ge y_j, forall i \ne j$. Do tính chất của hàm softmax (trong công thức hàm softmax là sự kết hợp của các hàm e mũ) nên đây là hàm tăng dẫn tới $z_i \ge z_j \iff w_i^Tx \ge w_i^Tx \iff (w_i - w_j)^Tx \ge 0$. Phương trình này chính là phương trình siêu phẳng trong không gian đặc trưng. Vậy các lớp được phân tách với nhau bởi một siêu phẳng (đường biên) có dạng tuyến tính.

Như vậy, mình đã đi sơ lược giới thiệu qua các hàm kích hoạt thường được sử dụng trong mạng nơ-ron. Bàn luận về vẻ đẹp của hàm softmax.

Thông qua bài viết này, các bạn sẽ nắm được những thông tin hữu ích sau:

• Ưu và nhược điểm của các hàm kích hoạt trong mạng nơ-ron.
• Tại sao chúng ta lại không quan tâm đến đạo hàm của hàm softmax trong các bài toán phân loại ảnh đa lớp.
• Làm sao bạn biết rằng điểm dữ liệu x được dự đoán sẽ rơi vào lớp nào chứ? Các lớp phân tách nhau dựa vào gì?