Tìm hiểu về Full text search
This post hasn't been updated for 4 years
Giới thiệu
Bình thường, khi chúng ta muốn tìm kiếm nội dung liên quan đến text, ta thường dùng câu query LIKE
SELECT column_name
FROM tables_name
WHERE column_name LIKE pattern;
Ví dụ khi muốn tìm kiếm 1 nội dung nào đó chứa từ thao thì ta hay làm thế này:
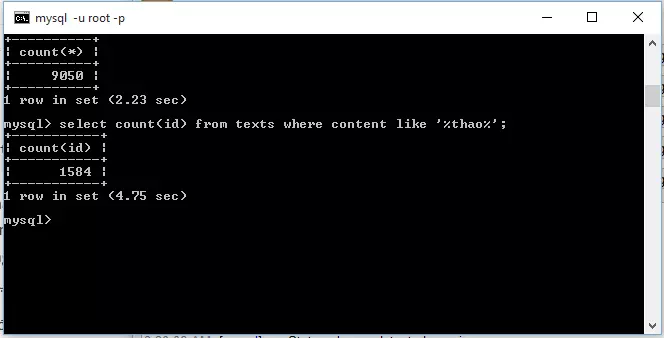
Sử dụng LIKE, chúng ta chỉ phải tìm kiếm ở 1 column đã định trước, do đó lượng thông tin phải tìm giới hạn lại chỉ trong các column đó. Khi dùng cách này, chúng ta phải so sánh chuỗi tìm kiếm với từng row trong DB, tức là chúng ta đã phải duyệt toàn bộ DB, do đó cách này có hạn chế:
- Chỉ search được trong row đã định trước.
- Hiệu năng không tốt, vì phải duyệt toàn bộ DB.
- Độ nhiễu cao: ví dụ muốn tìm kiếm
onethì kết quả sẽ làzone,phone,money,... - Không tìm được theo các từ đồng nghĩa: ví dụ muốn tìm
ô tô, thì kết quả liên quan tớixe hơi,4 bánhkhông được đưa ra. Hoặc các cụm từ ví dụ THPT (trung học phổ thông), CNTT (công nghệ thông tin),... - Có vấn đề với tìm kiếm tiếng Việt có dấu và không dấu.
Do đó, Full text search được đưa ra để giải quyết vấn đề.
Full text search
Full text search là cách tự nhiên nhất để tìm kiếm thông tin, hệt như Google, ta chỉ cần gõ từ khóa và nhấn enter thế là có kết quả trả về.
Để thực hiện Full text search, chúng ta cần tìm hiểu về các kỹ thuật cơ bản dùng trong Full Text search, sau khi tìm hiểu xong chúng ta có thể có cái hình dung rõ ràng về phương pháp tìm kiếm hay ho này.
Chúng ta cần tìm hiểu về:
- Inverted Index
- Tokenize
- Boolean Logic
- Ranking
Inverted Index
Inverted Index là kĩ thuật index theo đơn vị term(thay vì index theo đơn vị row giống như mysql). Cụ thể hơn, Inverted Index là một cấu trúc dữ liệu, nhằm mục đích mapping giữa term, và các document chứa term đó.
Ví dụ thế này cho dễ hiểu:
Ta có 3 documments d1, d2, d3 như thế này:
d1 = "có một con bò";
d2 = "có một đứa chăn trâu";
d3= "một con vịt";
Inverted Index của 3 documents đó sẽ được lưu dưới dạng như sau:
"có" => {d1, d2}
"một" => {d1, d2, d3}
"con" => {d1, d3}
"bò" => {d1}
"đứa" => {d2}
"chăn" => {d2}
"trâu" => {d2}
"vịt" => {d3}
Xong, giờ thì nếu ta muốn tìm kiếm 1 cụm từ "một con bò", với câu query LIKE bình thường, nó sẽ match với d1, tìm thấy, xong tiếp lại match với d2, không thấy, match với d3, không thấy => kết quả d1.
Nhưng ta đã dùng Inverted Index, vậy nên công việc bây giờ chỉ là tìm kiếm document chứa 3 term {"một", "con", "bò"}. Để làm việc này đơn giản là phép toán AND trong inverted index:
{d1, d2, d3} AND {d1} AND {d1} = {d1}
=> Kết quả là d1.
Ngoài ra, một điểm hay nữa chính là việc inverted index có khả năng flexible trong việc tìm kiếm, ví dụ giờ ta tìm cụm từ "bò con một", "con một bò",... thì kết quả vẫn là d1, trong khi LIKE sẽ không tìm thấy.
Tokenize
Cách index như trên hay thật, nhưng mà câu hỏi đặt ra là tách chuỗi làm sao để có được tập hợp index như vừa rồi? Để thực hiện việc này, có 2 kỹ thuật cơ bản giải quyết bài toán:
- N-Gram
- Morphological Analysis
N-Gram
N-gram là kĩ thuật tách một chuỗi thành các chuỗi con, thông qua việc chia đều chuỗi đã có thành các chuỗi con đều nhau, có độ dài là N.
Về cơ bản thì N thường nằm từ 1~3, với các tên gọi tương ứng là unigram(N = 1), bigram(N = 2), trigram(N = 3).
Ví dụ đơn giản là chúng ta có chuỗi "Hello world!", được phân tích thành bigram:
"Hello world!" => {"He", "ll", "o ", "wo", "rl", "d!"}
Tách chuỗi như này đơn giản lắm, có thể dùng PHP mà mình đã từng làm để thống kê văn bản:
public static function splitString($data, $numChar)
{
$content = self::processString($data->content);
$result = [];
$length = mb_strlen($content, 'UTF-8');
$length = $length - ($length % $numChar);
for ($i = 0; $i < $length; $i += $numChar) {
$char = mb_substr($content, $i, $numChar, 'UTF-8');
$result[] = $char;
}
return $result;
}
Đầu vào $numChar là 1, 2, 3 tương ứng với unigram, bigram, trigram.
Morphological Analysis
Về cơ bản Morphological Analysis là một kĩ thuật phổ biến trong xử lý ngôn ngữ tự nhiên (Natural Language Processing). Tức là chúng ta sẽ tách chuỗi thành những từ có nghĩa.
"Hello world!" => {"Hello", "world", "!"}
Để có được kết quả phân tích như trên, chúng ta cần phải có:
- một bộ từ điển tốt (để phân biệt được từ nào là có ý nghĩa, và thứ tự các từ thế nào thì có ý nghĩa).
- sử dụng các nghiên cứu sâu về xử lý ngôn ngữ tự nhiên.
N-Gram hay MA
Qua trình bày thì thấy MA tốt thật, kết quả tìm kiếm chính xác và gần gũi với chúng ta, còn N-Gram thì thấy có vẻ tệ. Nhưng để xây dựng MA thì cần một bộ từ điển tốt, để giúp cho máy tính có thể phân biệt được các từ có nghĩa, tức là từ điển chứa càng nhiều từ (terms) càng tốt.
Tuy nhiên ngôn ngữ thì mỗi ngôn ngữ lại có đặc trưng riêng, và không ngừng mở rộng, không ngừng thêm các từ mới. Việc chỉ sử dụng MA sẽ gây ra một tác dụng phụ là có rất nhiều từ không/chưa có trong từ điển, dẫn đến không thể index, và do đó sẽ không thể tiến hành tìm kiếm từ đó được.
Cách giải quyết tốt nhất là chúng ta sẽ kết hợp cả MA và N-gram. Cách kết hợp thế nào thì tùy trường hợp cụ thể.
Boolean Logic
Boolean logic sử dụng trong Search Engine thường sẽ gồm 3 phép toán chính là AND, NOT và OR.
Ta có một ví dụ giống ở trên:
D1 = "This is first document"
D2 = "This is second one"
D3 = "one two"
D4 = "This one is great"
D5 = "This two is great!"
"this" => {D1, D2, D4, D5}
"is" => {D1, D2, D4, D5}
"first" => {D1}
"document" => {D1}
"second" => {D2}
"one" => {D2, D3, D4}
"two" => {D3, D5}
Bây giờ ta muốn tìm This one, chúng ta sẽ tách câu truy vấn đó thành 2 token This và one.
Thông thường để cho dễ hiểu và phù hợp với logic của người dùng, thì space sẽ tương đương với logic AND, và bỏ qua xét việc chữ hoa, chữ thường, như vậy là kết quả của việc tìm kiếm sẽ là kết quả của tìm this AND kết quả của tìm one
{D1, D2, D4, D5} AND {D2, D3, D4} = {D2, D4}
Nếu muốn tìm This or one thì sao?
{D1, D2, D4, D5} AND {D2, D3, D4} = {D1, D3, D5}
Từ ví dụ trên chúng ta thấy rằng độ phức tạp của việc tìm kiếm lúc này sẽ chuyển thành:
- độ phức tạp của việc tách từ (đơn giản vì câu truy vấn nhập vào thường ngắn, hoặc nếu không thì cũng không quá khó)
- độ phức tạp của việc tìm kiếm chuỗi (đơn giản vì tuơng đuơng với việc tìm giá trị của 1 key trong inverted index)
- độ phức tạp của Boolean Logic dựa trên kết quả của tìm kiếm chuỗi (dựa vào các lý thuyết tập hợp, lý thuyết số lớn)
Ranking
Khi kết quả tìm kiếm chỉ có 1 hoặc 2 thì không vấn đề gì, nhưng kết quả là rất nhiều thì có vấn đề xảy ra, đó là đưa kết quả nào lên trước, hay chính là bài toán về Ranking.
Xếp rank không phụ thuộc vào mối quan hệ ngữ nghĩa giữa “query term” và “document”
Được xác định dựa trên lý thuyết "độ quan trọng của document phụ thuộc vào mối quan hệ giữa các document với nhau".
Ví dụ chúng ta có page rank để sắp sếp kết quả tìm kiếm website của Google. Ý tưởng của PageRank là “Page nào càng được nhiều link tới, và được link tới bởi các page càng quan trọng, thì score càng cao”. (Vì thế có 1 thủ thuật SEO là đi đặt link của mình vào càng nhiều website càng tốt).
Ngoài ra còn có HITS của Yahoo!
Xếp rank dựa vào mối quan hệ giữa “query term” và “document”
Các thuật toán thường dựa vào:
- tần suất xuất hiện của “query term” trong document
- dựa vào các đặc tính ngữ nghĩa (semantic) của query term
- thứ tự xuất hiện các từ trong “query term” và thứ tự xuất hiện trong “document”
- ...
Một trong những thuật toán được sử dụng nhiều nhất là TF-IDF (Term Frequency Inverse Document Frequency). Thuật toán này dựa vào ý tưởng thứ 1, là “query term” xuất hiện càng nhiều trong document, document sẽ có điểm càng cao.
Công thức:
TF − IDF(t, d, D) = TF(t, d) ∗ IDF(t, D)
Với:
TF(t, d) = frequency(t, d)
IDF(t, D) = log(N / ∥{d∈D:t∈d}∥)
Ở đây:
t: là query term,
d: là document cần được tính điểm,
D: là tập hợp tất cả các documents,
TF : tần suất xuất hiện của term t trong document d,
IDF : chỉ số này biểu hiện cho tần suất xuất hiện của term t trong toàn bộ các documents. t xuất hiện càng nhiều, chỉ số càng thấp (vì xuất hiện quá nhiều đồng nghĩa với độ quan trọng rất thấp).
Sử dụng học máy (Machine Learning)
Ý tưởng của việc sử dụng Machine Learning trong ranking là chúng ta sẽ sử dụng một mô hình xác suất để tính toán.

Nghĩa là chúng ta sẽ có input là một tập dữ liệu X để training, một mô hình đánh giá ranking M ban đầu, một hàm error để so sánh kết quả output X’ có được từ việc áp dụng model M vào query term, và một hàm boost để từ kêt quả của hàm error chúng ta có thể tính lại được model M. Việc này được lặp đi lặp lại mỗi lần có query để model M luôn luôn được cải thiện.
Thuật toán được sử dụng nhiều là Gradient Boosting Decision Tree và BM25
Kết luận
Sử dụng Full text search sẽ đem lại kết quả mong muốn nhất cho người sử dụng.
All Rights Reserved