Tìm hiểu về đồng bộ luồng trong java với bài toán: Bữa tối của các triết gia
Bài đăng này đã không được cập nhật trong 6 năm
Bài toán "Bữa tối của các triết gia" là một bài toán kinh điển về đồng bộ hóa. Nó trình bày quá trình cấp phát nhiều tài nguyên giữa các tiến trình mà không bị khoá chết và đói tài nguyên.
Trước khi đi giải quyết vấn đề của các triết gia. Tìm hiểu về Deadlock
Deadlock
Deadlock là một trạng thái mà ở đó một tập các tiến trình bị chặn vì mỗi tiến trình đang chiếm giữ tài nguyên và chờ đợi được cấp phát tài nguyên khác được giữ bởi tiến trình khác.
Nói cách khác, mỗi tiến trình trong hệ thống đang chờ để được cấp phát tài nguyên đang bị chiếm giữ bởi tài nguyên khác. Nếu tài nguyên đó không được giải phóng để tiến trình khác có thể sử dụng, thì tiến trình đang chờ lấy tài nguyên sẽ chờ mãi, chờ mãi dẫn tới Khóa chết ( Deadlock )
Để dễ hiểu hơn, hãy cùng nhau đến với một ví dụ:
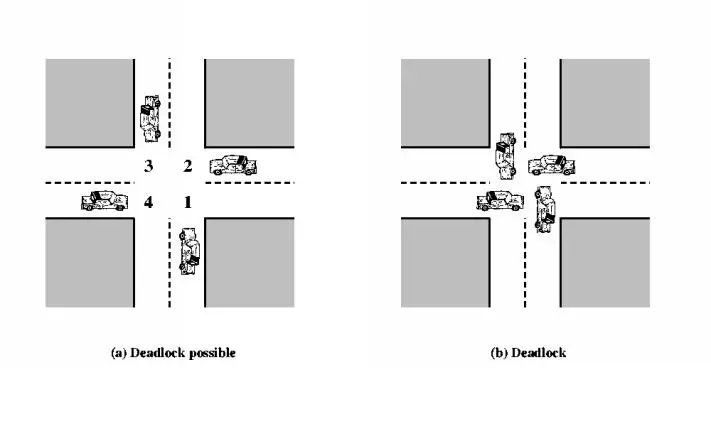
Ở ví dụ trên, ta có ngã tư kia là tài nguyên chung mà 4 chiếc xe cùng được chia sẽ. Các chiếc xe tượng trưng cho các luồng hoạt động đang cố chiếm tài nguyên là ngã tư để đi thẳng qua ngã tư. Khi không có sự đồng bộ, các chiếc xe đồng thời tiến vào ngã tư. Chiếc xe nào muốn tiến tới phía trước cũng phải chờ chiếc xe trước mặt mình đi qua. Cứ thế chờ mãi, chờ mãi. Điều đó dẫn tới việc Deadlock.
Các điều kiện phát sinh Deadlock
- Loại trừ tương hỗ (Mutual Exclusion): Tại một thời điểm, tài nguyên không thể chia sẽ được hệ thống cấp phát cho một tiến trình duy nhất. Tiến trình khác không thể sử dụng cho đến khi tài nguyên được giải phóng.
- Giữ và chờ (Hold and Wait) : Mỗi tiến trình trong tập hợp tiến trình đang giữ một tài nguyên và chờ đợi để được cấp phát một tài nguyên mới.
- Không có quyền ưu tiên (No Preemption): Một tiến trình không thể chiếm giữ tài nguyên cho đến khi tài nguyên đó được giải phóng bởi tiến trình đang sử dụng nó.
- Tồn tại chu kỳ chờ (Circular wait): Các tiến trình giữ một tài nguyên và chờ nhận một tài nguyên khác bởi tiến trình khác. Chúng nối đuôi nhau tạo thành vòng tròn. Chờ vô tận.
Deadlock chỉ xảy ra khi có đủ 4 điều kiện trên.
Bài toán Bữa tối của các triết gia
Có năm nhà triết gia, vừa suy nghĩ vừa ăn tối. Các triết gia ngồi trên một bàn tròn, trước mặt họ là các đĩa thức ăn, mỗi người một đĩa. Có 5 chiếc đũa được đặt xen kẽ giữa các triết gia. Như hình vẽ:

Bài toán được phát biểu như sau: "Khi một triết gia suy nghĩ, ông ta không giao tiếp với các triết gia khác. Thỉnh thoảng, một triết gia cảm thấy đói và cố gắng chọn hai chiếc đũa gần nhất (hai chiếc đũa nằm giữa ông ta với hai láng giềng trái và phải). Một triết gia có thể lấy chỉ một chiếc đũa tại một thời điểm. Chú ý, ông ta không thể lấy chiếc đũa mà nó đang được dùng bởi người láng giềng. Khi một triết gia đói và có hai chiếc đũa cùng một lúc, ông ta ăn mà không đặt đũa xuống. Khi triết gia ăn xong, ông ta đặt đũa xuống và bắt đầu suy nghĩ tiếp."
Tìm cách để không ai phải chết đói là vấn đề của bài toán.
Mô tả bài toán
Mỗi triết gia sẽ tượng trưng cho một tiến trình, và những chiếc đũa là tài nguyên của hệ thống. Các triết gia sẽ có 4 trạng thái lần lượt theo thứ tự là:
- Suy nghĩ ( Thinking )
- Lấy đũa ( Take Choptisks )
- Đang ăn ( Eating )
- Thả đũa ( Put Choptisks )
NOTE: Khi lấy được 2 chiếc đũa từ hai láng giềng gần nhất thì triết gia mới có thể ăn.
Ở đây mình dùng ngôn ngữ lập trình JAVA để mô tả bài toán. Để mô tả bài toán 5 tiến trình con được tạo ra đại diện cho 5 triết gia và 5 tài nguyên là 5 chia đũa đặt giữa các triết gia:
chops[0] = new Chopstick(0,200, 100, this);
chops[1] = new Chopstick(1,440, 100, this);
chops[2] = new Chopstick(2,490, 360, this);
chops[3] = new Chopstick(3,320, 420, this);
chops[4] = new Chopstick(4,150, 360, this);
phils[0] = new Philosophers(290, 60, chops[0], chops[1], this);
phils[1] = new Philosophers(480, 230, chops[1], chops[2], this);
phils[2] = new Philosophers(380, 430, chops[2], chops[3], this);
phils[3] = new Philosophers(170, 430, chops[3], chops[4], this);
phils[4] = new Philosophers(90, 230, chops[0], chops[4], this);
Mỗi tiến trình sẽ thực hiện việc lấy tài nguyên và trả lại sau khi một thời gian chiếm giữ, tương ứng với hành động lấy và trả lại các chiếc đũa của triết gia tương ứng:
while(true){
try{
//Thinking
changeImage("THINKING");
table.repaint();
//Take Chopsticks
leftChop.Acquire();
changeImage("LEFT");
table.repaint();
rightChop.Acquire();
// Eating
changeImage("EATING");
table.repaint();
sleep(EATING_TIME);
// Put Chopsticks
leftChop.Realease();
rightChop.Realease();
}
catch (InterruptedException e){}
}
Đề quản lý tài nguyên, mỗi chiếc đũa sẽ chứa 1 biến semaphore, khi đũa được lấy bởi 1 triết gia ta gọi hàm Acquire() để gắn cờ cho chiếc đũa đó, nhằm không cho triết gia khác lấy nó khi nó chưa được trả lại bằng cách gọi hàm Realease().
public void Acquire() throws InterruptedException
{
this.sem.acquire();
this.inUse = true;
}
public void Realease()
{
this.sem.release();
this.inUse = false;
}
Giải quyết tắc nghẽn
Semaphore là lời giải kinh điển cho bài toán bữa tối của các triết gia (dining philosophers), mặc dù nó không ngăn được hết các Deadlock. Để giải quyết Deadlock, ở vị trí cuối cùng ta sẽ cho triết gia đó được lấy đũa bên phải mình trước sau đó mới lấy đũa bên trái trong khi các triết gia khác sẽ lấy đũa bên trái trước. Điều đó chắc chắn rằng triết gia vị trí cuối luôn sẵn sàng ăn đầu tiên khi mà các triết gia khác đang cố lấy chiếc đũa bên phải của mình.
phils[0] = new Philosophers(290, 60, chops[0], chops[1], this);
phils[1] = new Philosophers(480, 230, chops[1], chops[2], this);
phils[2] = new Philosophers(380, 430, chops[2], chops[3], this);
phils[3] = new Philosophers(170, 430, chops[3], chops[4], this);
// The last philosopher picks up the right fork first
phils[4] = new Philosophers(90, 230, chops[0], chops[4], this);
kết quả là, không ai phải chết đói.
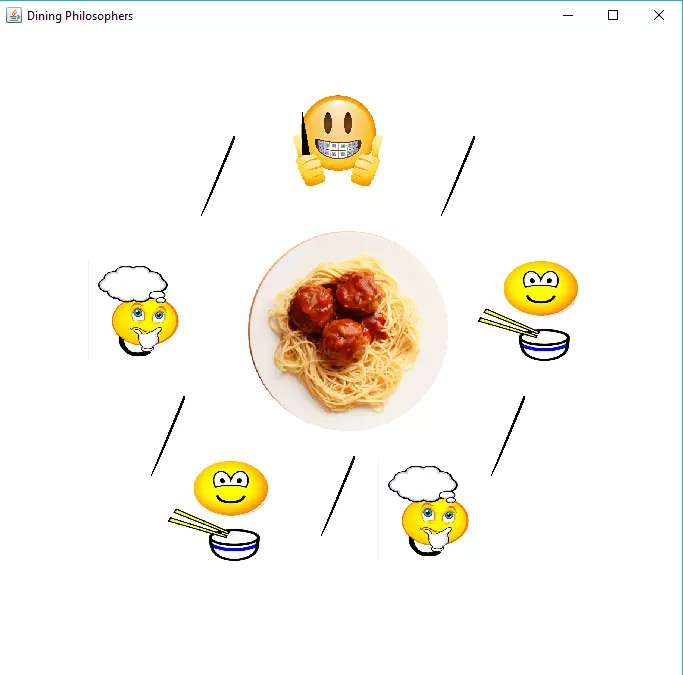
Một trường hợp cụ thể: Triết gia số 0: đang giữ một chiếc đũa bên trái mình Triết gia số 1: đang ăn khi đã có đủ hai chiếc đũa Triết gia số 3: đang suy nghĩ Triết gia số 4: đang ăn khi đã có đủ hai chiếc đũa Triết gia số 5: đang suy nghĩ
Hi vọng sau bài viết này, các bạn đã hiểu hơn về luồng cũng như việc đồng bộ luồng, giải quyết deadlock.
All rights reserved