Tìm hiểu thuật toán Quick Sort

Hôm nay mình đổi chủ đề sang thuật toán thay vì viết tiếp phần mạng máy tính. Lý do rất đơn giản vì cách đây 1 hôm có đứa em nó hỏi mình về thuật toán Quick Sort và thế là mình lên luôn ý tưởng viết về thuật toán nè coi như để ôn lại kiến thức cũ

Trước tiên mình nói qua chút về các loại thuật toán sắp xếp. Thuật toán sắp xếp được chia làm 2 loại:

• Sắp xếp trong (internal sort): họ dữ liệu được đưa toàn bộ vào bộ nhớ của máy tính
• Sắp xếp ngoài (external sort): họ dữ liệu không thể cùng lúc đưa toàn bộ vào bộ nhớ trong nhưng có thể đọc vào từng bộ phận từ bộ nhớ ngoài

Phân loại các thuật toán sắp xếp

• Thuật toán đơn giản (Độ phức tạp thuật toán - O(n^2)):
  • Sắp xếp chèn (insertion sort)
  • Sắp xếp nổi bọt ( bubble sort)
  • Sắp xếp lựa chọn (selection sort)
• Thuật toán hiệu quả (Độ phức tạp thuật toán - O(nlogn)):
  • Sắp xếp vun đống (Heap sort)
  • Sắp xếp trộn (Merge sort)
  • Sắp xếp nhanh (Quick sort)
• Thuật toán đăc biệt (Độ phức tạp thuật toán - O(n)):
  • Sắp xếp đếm (Counting Sort)
  • Sắp xếp phân cụm (Bucket Sort)
  • Sắp xếp cơ số (Radix Sort)
• Xử lý các tập dữ liệu lớn:
  • Sắp xếp ngoài (External sort)

Thuật toán Quick Sort

Là thuật toán sắp xếp dựa trên kỹ thuật chia để trị. Thuật toán được mô tả như sau:

• Base case: nếu dãy chỉ còn không quá 1 phần tử thì dãy đó đã được sắp xếp => không cần thao tác thêm gì cả
• Chia: ở thao tác này bao gồm 2 công việc:
  • Chọn 1 phần tử trong dãy làm phần tử chốt p (pivot)
  • Phân đoạn: chia dãy đã cho thành 2 dãy con, dãy con trái(L) sẽ gồm những phần tử nhỏ hơn phần tử chốt và dãy con phải(R) là những phần tử lớn hơn phần tử chốt.

• Trị: lặp lại 1 cách đệ quy thuật toán với 2 dãy con trái và phải
• Tổng hợp: dãy được sắp xếp L,p,R

Như vậy đối với thuật toán QS thì việc chọn phần tử chốt có vai trò quyết định đối với hiệu quả của thuật toán. Và người ta thường dùng các cách sau đây làm phần tử chốt:

• Chọn phần tử đầu tiên làm phần tử chốt
• Chọn phần tử cuối cùng làm phần tử chốt
• Chọn phần tử đúng giữa dãy làm phần tử chốt
• Chọn phần tử trung vị trong 3 phần tử đứng đầu, đứng cuối và đứng giữa làm phần tử chốt
• Chọn phần tử ngẫu nhiêu làm phần tử chốt

Cài đặt

Ở đây mình sẽ dùng javascript để thực hiện ví dụ. Mình sẽ demo thuật toán vs 3 cách chọn phần tử chốt là phần tử đầu, phần tử cuối và phần tử giữa.

Cách 1: Chọn chốt là phần tử đầu

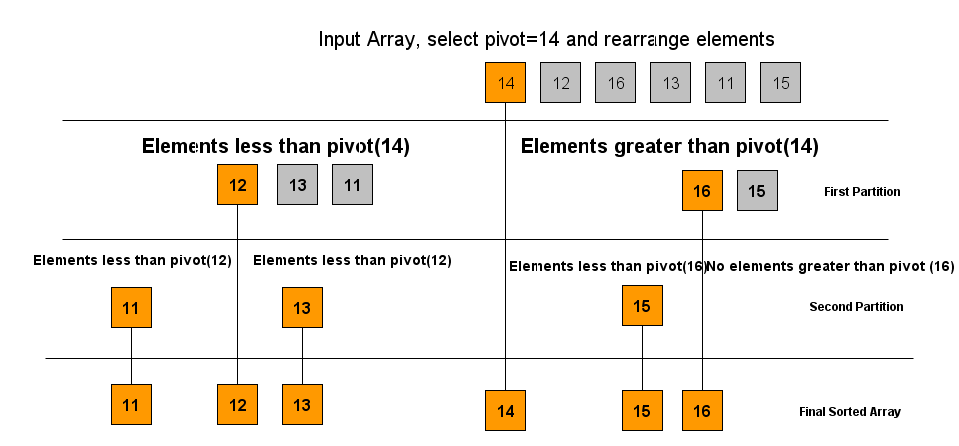
• Bước 1: Chọn phần tử đầu tiên làm chôt (14)
• Bước 2: Đưa những phần tử nhỏ hơn 14 vào mảng bên trái (12, 13, 11) và những phần tử lớn hơn 14 vào mảng bên phải (16, 15)
• Bước 3: thực hiện lại 2 bước trên với mảng bên trái và mảng bên phải (Easy phải không ạ)

quickSort = (unSortedArr) => {
        // nếu mảng không quá 1 phần tử thì mảng đó đã dc sx
        if (unSortedArr.length < 2) return unSortedArr;
       
        const pivot = unSortedArr[0]; //lấy phần tử dầu của mảng làm phần tử chốt
        const leftArr = []; // mảng chứa phần tử nhỏ hơn pivot
        const rightArr = []; // mảng chứa phần tử lớn hơn pivot
        let currentItem; // phần tử đang được xét
        
        // loop các phần tử còn lại trong mảng trừ phần tử pivot.
        // Do pivot là ptu đầu tiên nên i sẽ bắt đầu từ 1
        for (let i = 1; i < unSortedArr.length; i++) {     
            currentItem = unSortedArr[i];
            
            if (currentItem < pivot) {
                leftArr.push(currentItem);
            } else {
                rightArr.push(currentItem);
            }
        }
    
        return [...this.quickSort(leftArr), pivot, ...this.quickSort(rightArr)];
    }

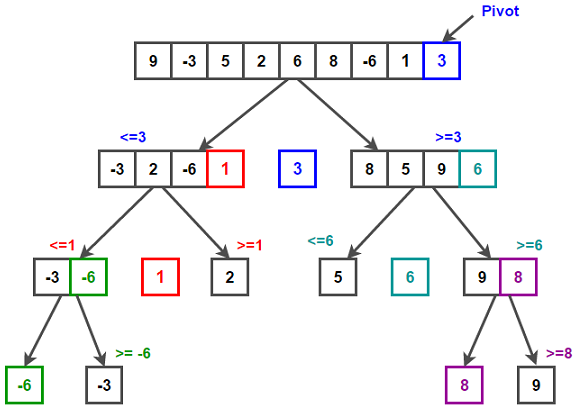
Cách 2: Chọn chốt là phần tử cuối

quickSort = (unSortedArr) => {
        if (unSortedArr.length < 2) return unSortedArr;
       
        const pivot = unSortedArr[unSortedArr.length - 1]; //phần tử cuối mảng làm chốt
        const leftArr = []; 
        const rightArr = []; 
        let currentItem;
        
        // Do pivot là ptu cuối nên length sẽ trừ đi 1 
        for (let i = 0; i < unSortedArr.length - 1; i++) {
            currentItem = unSortedArr[i];
            if (currentItem < pivot) {
                leftArr.push(currentItem);
            } else {
                rightArr.push(currentItem);
            }
        }
    
        return [...this.quickSort(leftArr), pivot, ...this.quickSort(rightArr)];
    }

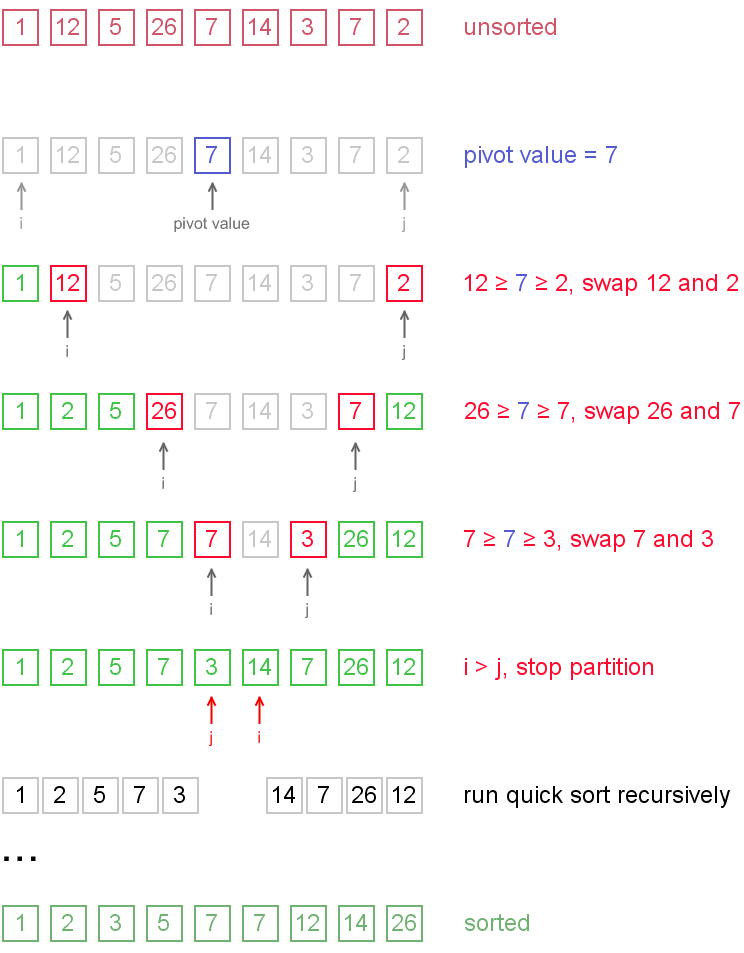
Cách 3: Chọn chốt là phần tử giữa

quickSort = (unSortedArr) => {
        if (unSortedArr.length < 2) return unSortedArr;
        
        // lấy phần tử giữa làm chốt
        const pivotIndex = Math.floor(unSortedArr.length / 2);
        const pivot = unSortedArr[pivotIndex]; 
        const leftArr = []; 
        const rightArr = []; 
        let currentItem;
        
        unSortedArr.splice(pivotIndex, 1); // loại bỏ ptu pivot trong mảng
        
        for (let i = 0; i < unSortedArr.length; i++) {
            currentItem = unSortedArr[i];
            if (currentItem < pivot) {
                leftArr.push(currentItem);
            } else {
                rightArr.push(currentItem);
            }
        }
    
        return [...this.quickSort(leftArr), pivot, ...this.quickSort(rightArr)];
    }

Độ phức tạp của thuật toán

Do hiệu quả của thuật toán phụ thuộc rất nhiều vào việc phần tử nào được chọn là phần tử chốt nên độ phức tạp thuật toán cũng phụ thuộc vào đó mà khác nhau.

• Phân đoạn không cân bằng: không có phần nào cả, một bài toán con có kích thước n-1 và bài toán kia có kích thước là 0. Đó là trường hợp xấu nhất xảy ra khi dãy đã cho là dãy đã được sắp xếp và phần tử chốt được chọn là phần tử đầu của dãy => độ phức tạp thuật toán sẽ là O(n^2)
• Phân đoạn hoàn hảo: phân đoạn luôn thực hiện dưới dạng phân thì đôi, mỗi bài toán con có kích thước là n/2 => độ phức tạp thuật toán là O(nlogn)
• Phân đoạn cân bằng: một bài toán con có kích thước n-k và bài toán kia có kích thước là k => độ phức tạp thuật toán là O(n)

Qua bài này hy vọng mọi người đã hiểu được sơ qua về thuật toán Quick sort là gì cũng như cách cài đặt nó trong js.

Thanks for reading

Tài liệu tham khảo: giáo trình cấu trúc dữ liệu vào giải thuật - ĐHBKHN