Tìm hiểu Quick Sort và Merge Sort thông qua JavaScript

Bài đăng này đã không được cập nhật trong 3 năm

Vào việc luôn nào (go)

1. Merge sort

1.1 Concept

Tương tự như tìm kiếm nhị phân, Merge sort là một thuật toán chia để trị.

Mục tiêu là chia nhỏ mảng của chúng ta thành các thành phần con và đệ quy tiếp tục chia nhỏ chúng cho đến khi chúng ta có nhiều thành phần đơn giản hơn mà chúng ta có thể dễ dàng ghép lại với nhau.

Merge sort được xây dựng dựa trên ý tưởng so sánh toàn bộ mảng thay vì các mục riêng lẻ.

Đầu tiên, chúng ta cần lấy toàn bộ mảng và chia nó thành nhiều mảng con bằng cách liên tục tách mọi thứ ra làm đôi cho đến khi mọi thứ nằm riêng trong mảng của chính nó.

Vì số lượng mảng con sẽ là bội số của số lượng mục trong mảng chính của chúng ta, nên độ phức tạp của thuật toán là O(nlogn).

Từ đó, chúng ta có thể bắt đầu merge chúng lại với nhau, vì cả hai mảng đã được sắp xếp, chúng ta có thể dễ dàng so sánh số nào trong mỗi mảng nhỏ hơn và đặt chúng vào đúng vị trí

Như bạn có thể thấy một nửa của mảng được hoàn thành trước nửa sau và nửa đầu của mỗi mảng trước nửa sau (các màu khác nhau đại diện cho các mảng khác nhau).

1.2 Practice Data

Đây là mảng dữ liệu để test bao gồm 50 phần tử chưa được sắp xếp theo thứ tự

const unsortedArr = [31, 27, 28, 42, 13, 8, 11, 30, 17, 41, 15, 43, 1, 36, 9, 16, 20, 35, 48, 37, 7, 26, 34, 21, 22, 6, 29, 32, 49, 10, 12, 19, 24, 38, 5, 14, 44, 40, 3, 50, 46, 25, 18, 33, 47, 4, 45, 39, 23, 2];

1.3 Merge

Để đơn giản hóa vấn đề, chúng ta có thể bắt đầu bằng cách tạo một hàm khởi tạo trước để hợp nhất hai mảng đã sắp xếp. Có nhiều cách khác nhau để thực hiện việc này nhưng mình thấy cách này ngắn gọn nhất.

Miễn là có các phần tử trong một trong hai mảng, kiểm tra xem phần tử đầu tiên trong một trong hai mảng có nhỏ hơn không, sau đó ném nó vào đã sắp xếp và xóa mục đó khỏi mảng bằng shift().

Khi thực hiện xong, nếu còn bất kỳ thứ gì còn sót lại, chẳng hạn như khi một mảng lớn hơn, hãy nối mảng đó vào phần cuối.

Vì vậy, cả hai mảng đang dần thu hẹp lại cho đến khi một trong số chúng trống với phần còn lại được ném vào cuối, vì nó đã được sắp xếp.

const merge = (arr1, arr2) => {
  let sorted = [];

  while (arr1.length && arr2.length) {
    if (arr1[0] < arr2[0]) sorted.push(arr1.shift());
    else sorted.push(arr2.shift());
  };

  return sorted.concat(arr1.slice().concat(arr2.slice()));
};

console.log(merge([2, 5, 10, 57], [9, 12, 13]));

1.4 Sorting

Đến phần này thì dễ dàng hơn rồi, chúng ta có thể sử dụng một hàm đệ quy để liên tục cắt mảng của chúng ta làm đôi, sử dụng slice() để lưu dữ liệu ở hai phía phần tử ở giữa.

Nó sẽ trở lại khi chúng ta có các mảng 1 mục, sau đó chúng ta sẽ sử dụng hàm merge bên trên để bắt đầu xây dựng lại chúng thành một mảng lớn, với mỗi lần merge sẽ sắp xếp lại chúng.

const mergeSort = arr => {
  if (arr.length <= 1) return arr;
  let mid = Math.floor(arr.length / 2),
      left = mergeSort(arr.slice(0, mid)),
      right = mergeSort(arr.slice(mid));

  return merge(left, right);
};

console.log(mergeSort(unsortedArr));

Bạn có thể sử dụng console của trình duyệt để test thử

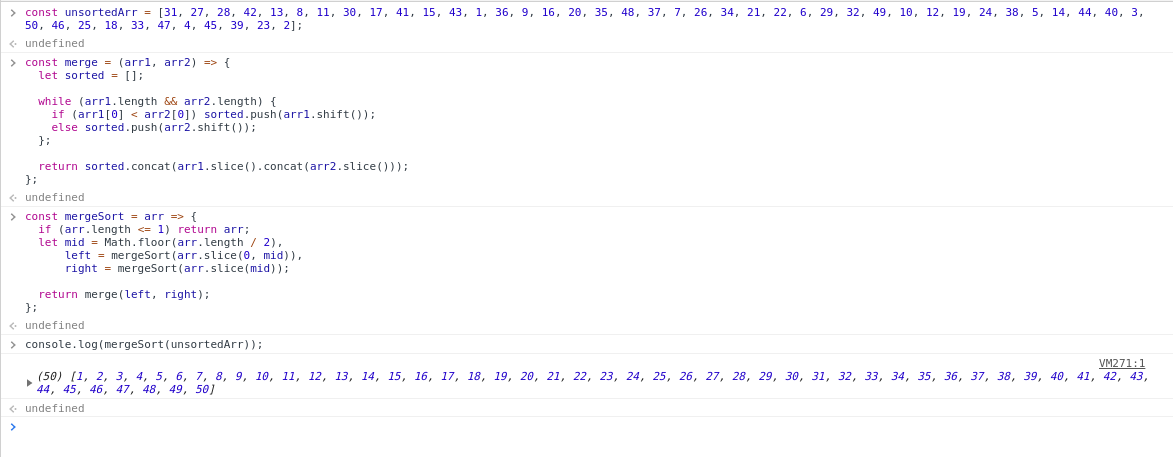
Done rồi !!!!

2. Quick sort

2.1 Concept

Quick sort là một trong những thuật toán kém trực quan hơn, vì vậy đây sẽ à một cái nhìn tổng quan rất đơn giản.

Chúng ta chọn một số, được gọi là trục (pivot), tiếp theo sẽ so sánh mọi số với nhau khi chúng ta lặp lại các phần tử.

Mục đích là tổ chức lại mảng để nó được chia thành hai nửa, với mọi thứ trong mỗi nửa nhỏ hơn hoặc lớn hơn pivot.

Khi pivot quay ở vị trí cuối cùng, chúng ta sẽ chuyển sang làm điều tương tự với một pivot mới, với mọi pivot được cố định tại chỗ cho đến khi mọi phần tử đều là pivot quay ít nhất một lần.

Giống như Merge sort, độ phức tạp trung bình là O (nlogn), vì vậy tùy thuộc vào giải thuật mà bạn muốn mà thôi.

2.2 Practice Data

Giống với merge sort, ta cũng có mảng gồm 50 phần tử chưa đựoc sắp xếp

const unsortedArr = [31, 27, 28, 42, 13, 8, 11, 30, 17, 41, 15, 43, 1, 36, 9, 16, 20, 35, 48, 37, 7, 26, 34, 21, 22, 6, 29, 32, 49, 10, 12, 19, 24, 38, 5, 14, 44, 40, 3, 50, 46, 25, 18, 33, 47, 4, 45, 39, 23, 2];

2.3 Pivot

Trước tiên, chúng ta sẽ cần function lựa chọn pivot.

Con trỏ chỉ là một hình thức đánh dấu chỗ cho pivot. Mỗi khi vòng lặp thực hiện, mỗi phần tử được so sánh với pivot và nếu nó nhỏ hơn, nó sẽ được hoán đổi với con trỏ.

Mỗi lần chúng ta làm điều này là để đảm bảo rằng con trỏ đi trước mọi thứ luôn nhỏ hơn pivot và trước mọi thứ lớn hơn.

Khi thực hiện hoàn tất và mảng của chúng ta được phân vùng, thì chúng ta có thể gán pivot cho index của con trỏ làm vị trí cuối cùng của nó.

Hoán đổi của chúng tôi hoạt động bằng cách chỉ định lại các chỉ mục của từng mục với chỉ mục của nhau, không có gì quá điên rồ.

const pivot = (arr, start, end) => {
  const swap = (list, a, b) => [list[a], list[b]] = [list[b], list[a]];

  let pivot = arr[start],
      pointer = start;

  for (let i = start; i < arr.length; i++) {
    if (arr[i] < pivot) {
      pointer++;
      swap(arr, pointer, i);
    }
  };
  swap(arr, start, pointer);

  return pointer;
}

2.4 Quick Sort

Chúng ta sẽ sử dụng hàm pivot bên trên để lấy phần tử được sắp xếp đầu tiên từ mảng cho trước.

Cùng với đó, chúng ta sẽ chạy đệ quy quickSort để thực hiện quy trình tương tự trên nửa đầu của mảng được phân vùng (partition), quá trình này sẽ lặp lại cho đến khi không còn gì để sắp xếp, sau đó thực hiện tương tự cho nửa còn lại.

Khi cả hai được thực hiện xong, mảng được sắp xếp đầy đủ của chúng ta sẽ được trả về.

const quickSort = (arr, start = 0, end = arr.length) => {
  let pivotIndex = pivot(arr, start, end);

  if (start >= end) return arr;
  quickSort(arr, start, pivotIndex);
  quickSort(arr, pivotIndex + 1, end - 1);

  return arr;
};

console.log(quickSort(unsortedArr));

Done tiếp