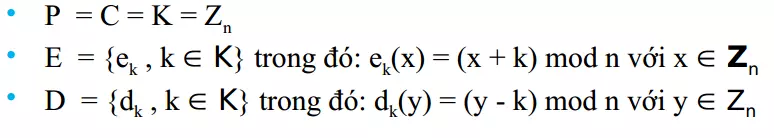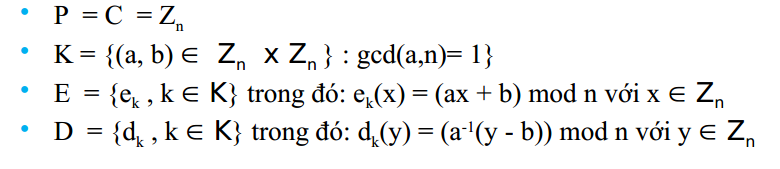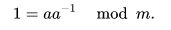Tìm hiểu một số loại mã hóa cổ điển
Bài đăng này đã không được cập nhật trong 6 năm
Giới thiệu
Ở bài viết này mình xin giới thiệu về một số loại mã hóa cổ điển như:
-
Mã hóa dịch vòng
-
Mã hóa thay thế
-
Mã hóa Affine
trước hết chúng ta cần biết xem mã hóa là gì, mã hóa là quá trình dùng để biến thông tin từ dạng này sang dạng khác và ngăn những người không phận sự tiếp cận vào thông tin đó. Bản thân việc mã hóa không ngăn chặn việc thông tin bị đánh cắp, có điều thông tin đó lấy về cũng không xài được, không đọc được hay hiểu được vì đã được làm biến dạng đi rồi. Mã hóa sẽ mang lại tính an toàn cao hơn cho thông tin, đặc biệt là trong thời đại Internet ngày nay, khi mà thông tin phải đi qua nhiều trạm trung chuyển trước khi đến được đích. Nếu không có mã hóa, khả năng thông tin của bạn sẽ bị ai đó xem trộm trong quá trình truyền tải rồi lợi dụng để làm việc xấu.
Đối với những người mới tìm hiểu về mã hóa thì tìm hiểu về mã hóa cổ điển có lẽ là cách tiếp cận dễ dàng nhất. Mã hoá cổ điển là cách đơn giản nhất, tồn lại lâu nhất trên thế giới và không cần khóa bảo mật, chỉ cần người gửi và người nhận cùng biết về thuật toán này là được.
Sau đây mình sẽ đi vào một số loại mã hóa cổ điển cụ thể 
Mã Hóa dịch vòng
Mã hóa dịch vòng là một bộ năm (P, C, K, E, D) thỏa mãn:
Ví dụ : giải mã và mã hóa đoạn text: p = " abcde" với k = 5 ( p ở đây là các kí tự thường trong bảng chữ cái tiếng anh )
Quy ước: Số thứ tự của các chữ cái trong bảng chữ cái tiếng anh như sau: a = 0, b = 1, …, z= 25 nên t có :
-
n = 26
-
p = "abcde"
-
k = 5 Xách định bản mã c = ?
-
Bước 1 : Đổi các ký tự trong p sang thứ tự của chúng trong bảng chữ cái.
a = 0 , b=1, c= 2, d= 3, e = 4 -
Bước 2 : Tiến hành mã hóa bản rõ p với khóa k = 5
-
Bước 3: xác định bản mã c
=> c = "fghij"
Bài toán ngược:
- cho bản mã c = "fghij"
- k =5
- n =26
- xác đinh bản rõ p
Quy ước: Số thứ tự của các chữ cái trong bảng chữ cái tiếng anh như sau: a = 0, b = 1, …, z= 25
Bước 1: đổi các ký tự trong c sang thứ tự của chúng trong bảng
chữ cái.
Bước 2: tiến hành giải mã bản mã c với khóa k = 5
Bước 3: xác định bản rõ p
=> p = "abcde"
Mã hóa thay thế
Mã hóa thay thế là một bộ năm thành phần (P, C, K, E, D) thỏa mãn:
Ví dụ : giải mã với
- c = "yudhk"
- pi được mô tả ở bảng dưới
- xác định c = ?
Ta có c:
=> c = “yudhk”
Tương tự như trên đối với bài toán ngược cho:
- c = “yudhk”
- π -1 được mô tả như ở bảng bên dưới
Ta xác định được p = “abcde”
Mã hóa Affine
Mã hóa Affine là một bộ năm (P, C, K, E, D) thỏa mãn:
Ví dụ : mã hóa
- p = "abcde"
- k = (a, b) = (5, 3); n =26
- Tính c = ?
Ta có c :
| p | a | b | c | d | e |
|---|---|---|---|---|---|
| x | 0 | 1 | 2 | 3 | 4 |
| (5x +3 ) mod 26 | 3 | 8 | 13 | 18 | 23 |
| c | d | i | n | s | x |
=> c= "dinsx"
Tương tự với bài toán ngược, cho
- "dinsx"
- k = (a, b) = (5, 3); n= 26; tính được a mũ -1 = 21 từ công thức :
- tính p = ?
ta có p :
| c | d | i | n | s | x |
|---|---|---|---|---|---|
| y | 3 | 8 | 13 | 18 | 23 |
| (21(y-3))mod 26 | 0 | 1 | 2 | 3 | 4 |
| p | a | b | c | d | e |
=> p = "abcde"
Lời kết
Như vậy mình đã giới thiệu với các bạn 3 thuật toán mã hóa cổ điển dành cho những bạn mới bắt đầu tìm hiểu về mã hóa. Bài viết còn nhiều thiếu sót rất mong được sự đóng góp từ các bạn, mọi thắc mắc các bạn có thể comment bên dưới để mình và mọi người cùng giải đáp. Cảm ơn các bạn đang quan tâm và đón đọc.
All rights reserved