Thuật toán chuỗi Fibonacci △

Bài đăng này đã không được cập nhật trong 5 năm

Có lẽ là một trong những thuật toán nổi tiếng nhất từ trước đến nay, nhưng vẫn còn rất nhiều người phải gặp khó khăn khi cố gắng tìm một giải pháp hiệu quả. Hãy để mình giới thiệu cho bạn về chuỗi Fibonacci.

Statement
Cho 1 số N, trả về số fibonacci thứ N, trong đó chuỗi đó như sau:

0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, ...

Sau khi xem qua, bạn có thể dễ dàng nhận thấy mỗi phần tử trong chuỗi là tổng của 2 phần tử liền trước nó.

F(n) = F(n-1) + F(n-2)

First implementation
Vì vậy, bây giờ chúng ta sẽ implement đoạn code đầu tiên, chúng ta sẽ sử dụng một vòng lặp đơn giản để đi đến lời giải.

function fibonacci(num){
  var a = 1, b = 0, temp;

  while (num > 0){
    temp = a;
    a = a + b;
    b = temp;
    num--;
  }

  return b;
}

Đây có lẽ là giải pháp đầu tiên trong đầu của bạn. Phần quan trọng ở đây là chúng ta tính toán số tiếp theo bằng cách thêm số hiện tại vào số cũ.
Và tin tốt là nó có độ phức tạp O(n). Nhưng bây giờ hãy để thử xem một số cách khác để tiếp cận vấn đề.

Dùng đệ quy
Bây giờ hãy để xem nếu chúng ta có thể làm cho nó trông xịn hơn, bây giờ chúng ta sẽ sử dụng đệ quy để làm điều đó.

function fibonacci(num) {
  if (num <= 1) return num;

  return fibonacci(num - 1) + fibonacci(num - 2);
}

Dễ đúng không? chúng ta chỉ giải quyết vấn đề trong 2 dòng code, nhưng hãy nhìn sâu hơn và xem những gì thực sự xảy ra.

Base case: chúng ta chỉ cần kiểm tra xem giá trị nhỏ hơn 1 để trả về 2 trường hợp đầu tiên.
Tin xấu là, chúng ta đã tăng độ phức tạp thời gian của thuật toán gần như là trường hợp xấu nhất. O(2^N), có nghĩa là việc triển khai hiện tại của chúng ta là theo cấp số nhân.

Memoization
Cuối cùng, và theo cách tiếp cận đệ quy, chúng ta sẽ sử dụng memoization để cải thiện độ hiệu quả của thuật toán.
Thay đổi này sẽ tăng độ phức tạp không gian của thuật toán mới của chúng ta thành O (n) nhưng sẽ giảm đáng kể độ phức tạp thời gian xuống O(2N).

function fibonacci(num, memo) {
  memo = memo || {};

  if (memo[num]) return memo[num];
  if (num <= 1) return num;

  return memo[num] = fibonacci(num - 1, memo) + fibonacci(num - 2, memo);
}

Bendmark
Sử dụng 50 làm số đầu vào và so sánh 3 cách trên:

While loop

Time complexity: O(N)
Space complexity: Constant
Function calls: 51
Time needed: 0.000001ms

Recursion

Time complexity: O(2^N)
Space complexity: O(n)
Function calls: 20.365.011.074
Time needed: 176.742ms

Memoization

Time complexity: O(2N)
Space complexity: O(n)
Function calls: 99
Time needed: 0.000001ms

Kết luận
Đây chỉ là một ví dụ về cách thiết kế, cải thiện và phân tích thuật toán, trong trường hợp này là chuỗi Fibonacci, đủ đơn giản để hiểu và đáng ngạc nhiên khi thấy hiệu suất tăng mà ta đạt được chỉ với một số thay đổi nhỏ.

Một số cách tiếp cận khác
Chúng ta có thể dùng công thức Binet để tính số fibonacci thứ N.

function fibonacci(n) {
 return Math.round(
 (Math.pow((1 + Math.sqrt(5)) / 2, n) -
 Math.pow(-2 / (1 + Math.sqrt(5)), n)) / 
 Math.sqrt(5)
 );
}

Hoặc chúng ta cũng có thể ứng dụng phép nhân ma trận, để hiểu kỹ hơn các bạn có thể google nó nhé, lý thuyết như hình bên dưới , cũng khá đơn giản thôi, với độ phức tạp O(logN)

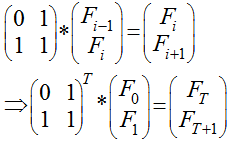
// Hàm nhân ma trận
function multiply(mA, mB) {
	let m = [[], []];
	for (let i = 0; i <= 1; i++) {
      for (let j = 0; j <= 1; j++) {
        m[i][j] = 0;
        for (let k = 0; k <= 1; k++) {
          m[i][j] = (m[i][j] + mA[i][k] * mB[k][j]);
        }
      }
    }
    return m;
}

// Hàm tính lũy thừa bậc n ma trận m
function power(m, n) {
  if (n==1) return m;
  if (n%2!=0) return multiply(power(m, n-1) ,m);
  let r = power(m,n/2);
  return multiply(r, r);
}

// Tính số fibonacci thứ n
// let A = [[1,1],[1,0]];
// fib(0) = 0, fib(1) = 1
// let B = [[0], [1]];
// multiply(power(A, n), B))[0][0];

Vậy thôi, qua đây mình cũng chỉ giới thiệu một số cách để giải, còn nhiều cách khác, hay ho hơn, xịn hơn các bạn có thể tự nghiên cứu thêm nhé. △

Algorithm JavaScript

Mục lục