I. Rijndael S-box là gì ?

Trong mật mã học, S-box (substitution-box) là thành phần cơ bản của thuật toán mã khóa đối xứng, được dùng để thực hiện các phép thay thế phi tuyến. Trong mã khối, chúng thường được sử dụng để che giấu mối quan hệ giữa khóa mật mã và bản mã — tính hỗn loạn do Shannon đề xuất. Rijndael S-box là một sbox được sử dụng trong mật mã Rijndael, dựa trên đó để tạo ra thuật toán mã hóa AES.

II. Cách tạo Rijndael S-box

Bảng S-box thuận được sinh ra bằng việc xác định nghịch đảo cho một giá trị nhất định trên GF(2^8) = GF(2) [x]/(x^8 + x^4 + x^3 + x + 1) (trường hữu hạn Rijindael). Giá trị 0 không có nghịch đảo thì được ánh xạ với 0. Những nghịch đảo được chuyển đổi thông qua phép biến đổi affine, công thức của phép biến đổi như sau:

Đầu vào của phép biến đổi là x và đầu ra là y, với mỗi giá trị x(0<= x <= 255) thì ta sẽ nhận được một giá trị y tương ứng. Dưới đây là bảng S-box được sinh ra từ công thức trên.

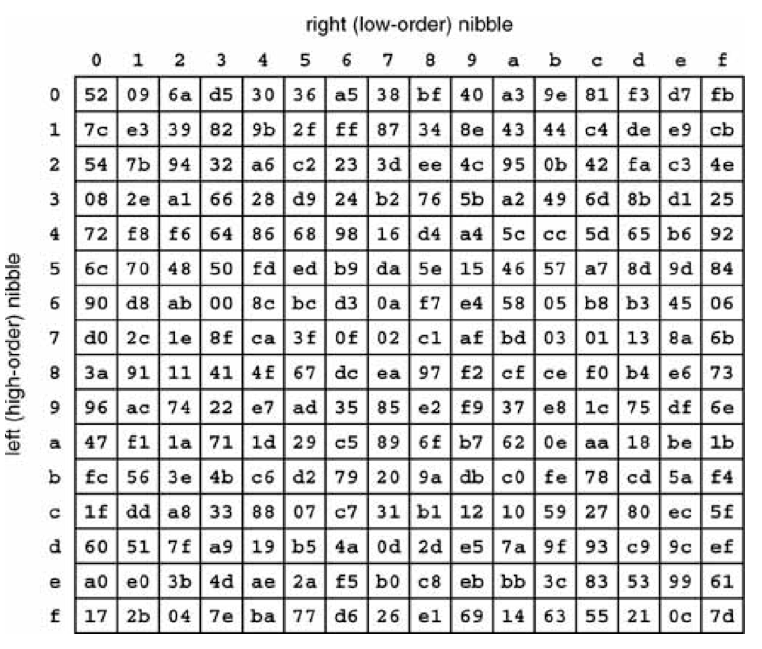
Để có một bảng S-box như trên thì ta có hai cách: một là coppy nó về sử dụng luôn, hai là tự tạo nó bằng code. Trong bài này mình sẽ hướng dẫn cách thứ hai, còn cách thứ nhất thì các bạn tự search google nhé.

1. Tạo các biến cần thiết

//y = Ax^-1 + B
int A[8][8] = {
    {1,0,0,0,1,1,1,1},
    {1,1,0,0,0,1,1,1},
    {1,1,1,0,0,0,1,1},
    {1,1,1,1,0,0,0,1},
    {1,1,1,1,1,0,0,0},
    {0,1,1,1,1,1,0,0},
    {0,0,1,1,1,1,1,0},
    {0,0,0,1,1,1,1,1}};
int B[8] = {1,1,0,0,0,1,1,0};

int arrayX[8];//biến x đầu vào
int c[8];
int aff[8];//kết quả biến y đầu ra
int sbox[16][16];

2. Tạo các hàm bổ trợ để tạo S-box

//đếm số bit trong x
int numberBits(int x){
    int nb = 0;
        while (x != 0) {
            nb += 1;
            x >>= 1;
        }
	return nb;
}

int modPolynomial(int x, int m) {
    int nbm = numberBits(m);
        while(true) {
            int nbx = numberBits(x);
            if(nbx < nbm) {
                return x;
            }
            int mshift = m << (nbx - nbm);
            x ^= mshift;
        }
}

int mulPolynomial(int x,int y) {
    int z = 0;
	while (x != 0) {
        if ((x & 1) == 1)
            z ^= y;
	y <<= 1;
	x >>= 1;

    }
    return z;
}
//tính x^-1
int xinv(int n) {
    int m = 283;
    for (int i = 1; i < 256; i++) {
        if(modPolynomial(mulPolynomial(n,i), m) == 1) {
            return i;
        }
    }
    return 0;
}

//chuyển x từ Dec -> Bin
void toBinary(int n)
{
    string r;

    while(n != 0) {
        r = (n % 2 == 0 ? "0" : "1") + r;
        n /= 2;
    }

    for(int i = 0; i < r.length(); i++) {
        arrayX[8 - r.length() + i] = r[i] - '0';
    }
}
// chuyển x từ Bin -> Dec
int binaryToInt(int x[]) {\
    int n = 0;
    int d = 0;
    for (int i = 7; i >= 0; i--) {
        n += pow(2, d) * x[i];
        d++;
    }
    return n;
}

void mulMatrix(int a[8][8], int b[8]) {
    for (int i = 0; i < 8; i++) {
        for (int j = 0; j < 8; j++) {
            c[i] += a[i][j] * b[8 - j - 1];
        }
        c[i] = c[i] % 2;
    }
}

void mod(int a[], int b[]) {
    for (int i = 0; i < 8; i++) {
        c[i] = (a[i] + c[i]) % 2;
    }
}

void invertArray() {
    for(int i = 0; i < 8; i++) {
        aff[i] = c[8-i-1];
    }
}

3. Tạo S-box Mọi thứ đã có đủ ta bắt tay vào tạo s-box.

• Đầu tiên ta tạo phép biến đổi affine

//x[] là x^-1
void affin(int x[]) {
    mulMatrix(A, x);
    mod(B, c);
    invertArray();
}

• Cuối cùng là ta tạo S-box

void createSbox() {
    for(int i = 0; i < 16; i++) {
        for(int j = 0; j < 16; j++) {
            for(int k = 0; k < 8; k++) {
            arrayX[k] = c[k] = aff[k] = 0;//Khởi tạo các giá trị ban đầu
        }
        toBinary(xinv(i *16 + j));//tìm nghịch đảo của x và chuyển sang dạng nhị phân, kết quả lưu trong arrayX
        affin(arrayX);//cho x^-1 qua phép biến đổi affine, kết quả lưu trong aff
        sbox[i][j] = binaryToInt(aff);//Chuyển kết quả vừa tính sang thập phân và lưu vào sbox
        }
    }
}

Và đây là thành quả chúng ta nhận được:

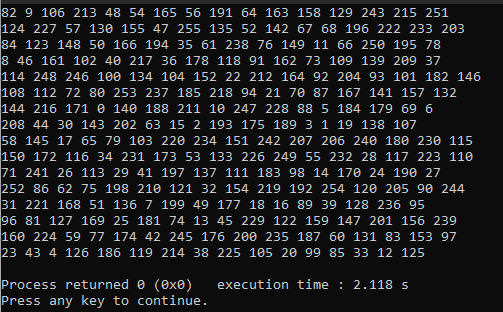
Kết

Trong bài viết này mình đã hướng dẫn các bạn cách để tự tạo được một Rijndael S-box, cảm ơn các bạn đã theo dõi!