Tám cấu trúc dữ liệu phổ biến trong Javascript

Với những ai đang cần tìm hiểu thêm một vài kiến thức cơ bản về khoa học máy tính, đặc biệt là cấu trúc dữ liệu và giải thuật, thì bài viết này sẽ có ích khi mô tả một bức tranh sinh động về cách thức hoạt động của một số loại cấu trúc dữ liệu phổ biến.

1. Stack (Ngăn xếp)

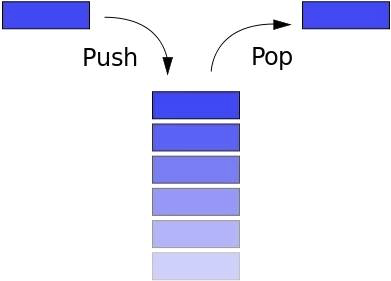
Stack hoạt động theo nguyên tắc LIFO (Last In First Out - Ra trước vào sau). Ví dụ nếu bạn có một chồng sách thì cuốn sách đặt trên cùng sẽ luôn được lấy trước cuốn sách đặt dưới cùngcùng. Hoặc khi truy cập vào trình duyệt web, nút back thường sẽ dẫn bạn đến trang được duyệt gần nhất trước đó.

Các phương thức phổ biến của Stack đó là:

• Push: Thêm một phần tử mới.
• Pop: Lấy một phần tử ở phía trên cùng của stack và trả về giá trị của phần tử đó.
• Peek: Trả lại phần tử ở phía trên cùng của stack.
• Length: Trả về số lượng phần tử trong Stack.

Mảng trong Javascript có các thuộc tính của Stack, nhưng ở đây chúng ta sẽ xây dựng một Stack bằng cách sử dụng function Stack():

function Stack() {
this.count = 0;
  this.storage = {};

  this.push = function (value) {
    this.storage[this.count] = value;
    this.count++;
  }

  this.pop = function () {
    if (this.count === 0) {
      return undefined;
    }
    this.count--;
    var result = this.storage[this.count];
    delete this.storage[this.count];
    return result;
  }

  this.peek = function () {
    return this.storage[this.count - 1];
  }

  this.size = function () {
    return this.count;
  }
}

2. Queue (Hàng đợi)

Queue hoạt động theo nguyên tắc FIFO (First In First Out - Vào trước ra trước). Ví dụ khi bạn xếp hàng chờ xe buýt, người đầu tiên trong hàng đợi sẽ luôn được lên trước. Các phương thức của Queue đó là:

• Enqueue: Thêm phần tử vào cuối hàng đợi.
• Dequeue: Xoá phần tử đầu tiên của hàng đợi.
• Front: Trả về phần tử đầu tiên.
• isEmpty: Xác định xem hàng đợi có đang rỗng không.
• Size: Lấy số phần tử trong hàng đợi.

Mảng trong Javascript có một vài thuộc tính của Queue, vì thế chúng ta có thể sử dụng mảng này để xây dựng một ví dụ cho Queue:

function Queue() {
  var collection = [];
  this.print = function () {
    console.log(collection);
  }
  this.enqueue = function (element) {
    collection.push(element);
  }
  this.dequeue = function () {
    return collection.shift();
  }
  this.front = function () {
    return collection[0];
  }

  this.isEmpty = function () {
    return collection.length === 0;
  }
  this.size = function () {
    return collection.length;
  }
}

Priority Queue (Hàng đợi ưu tiên)

Queue có một phiên bản nâng cao khác. Các phần tử được phân bổ ưu tiên sẽ được sắp xếp theo mức độ ưu tiên:

function PriorityQueue() {

  ...

  this.enqueue = function (element) {
    if (this.isEmpty()) {
      collection.push(element);
    } else {
      var added = false;
      for (var i = 0; i < collection.length; i++) {
        if (element[1] < collection[i][1]) {
          collection.splice(i, 0, element);
          added = true;
          break;
        }
      }
      if (!added) {
        collection.push(element);
      }
    }
  }
}

Kiểm tra:

var pQ = new PriorityQueue();
pQ.enqueue([ gannicus , 3]);
pQ.enqueue([ spartacus , 1]);
pQ.enqueue([ crixus , 2]);
pQ.enqueue([ oenomaus , 4]);
pQ.print();

Kết quả:

[
  [  spartacus , 1 ],
  [  crixus , 2 ],
  [  gannicus , 3 ],
  [  oenomaus , 4 ]
]

3. Linked List (Danh sách liên kết)

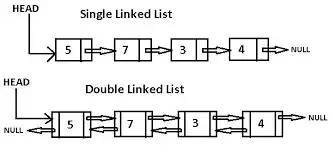
Một danh sách liên kết (linked list) là một chuỗi các cấu trúc dữ liệu, với mỗi node bao gồm hai phần thông tin: dữ liệu của node và tham chiếu đến node kế tiếp trong chuỗi. Danh sách liên kết và mảng quy ước là hai cấu trúc dữ liệu tuyến tính với lưu trữ tuần tự. Tất nhiên chúng cũng có sự khác biệt nhất định:

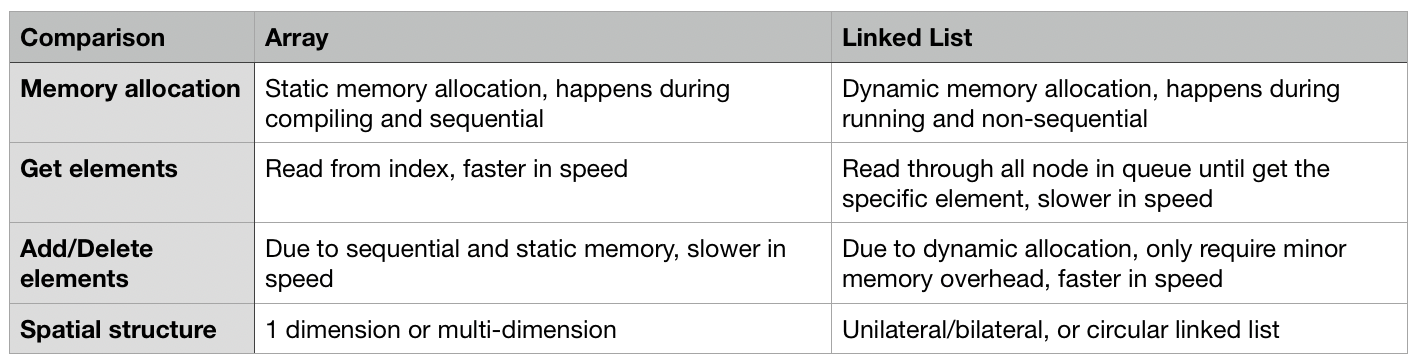
Một danh sách liên kết một chiều thông thường bao gồm các phương thức:

• size: Trả về số lượng các node trong list.
• head: Trả về phần tử đầu.
• add: Thêm một node mới ở đuôi.
• remove: Xoá một node bất kỳ.
• indexOf: Trả về vị trí của một node.
• elementAt: Trả node về vị trí của nó.
• addAt: Insert node vào một vị trí đặc biệt cụ thể.
• removeAt: Xoá node tại vị trí đặc biệt cụ thể.

/** Node in the linked list **/
function Node(element) {  
    // Data in the node
    this.element = element;  
    // Pointer to the next node 
    this.next = null;
}
    function LinkedList() {  
        var length = 0;  
        var head = null;  
        this.size = function () {    
            return length;  
        }  
        this.head = function () {    
            return head;  
        }  
        this.add = function (element) {    
            var node = new Node(element);    
            if (head == null) {      
                head = node;    
            } else {      
                var currentNode = head;      
                while (currentNode.next) {        
                    currentNode = currentNode.next;      
                }      
                currentNode.next = node;    
            }    
            length++;  
        }  
        this.remove = function (element) {    
            var currentNode = head;    
            var previousNode;    
            if (currentNode.element === element) {      
                head = currentNode.next;    
            } else {      
                while (currentNode.element !== element) {        
                    previousNode = currentNode;        
                    currentNode = currentNode.next;      
                }      
                previousNode.next = currentNode.next;    
            }    
            length--;  
        }  
        this.isEmpty = function () {    
            return length === 0;  
        }  
        this.indexOf = function (element) {    
            var currentNode = head;    
            var index = -1;    
            while (currentNode) {      
                index++;      
                if (currentNode.element === element) {        
                    return index;      
                }      
                currentNode = currentNode.next;    
            }    
            return -1;  
        }  
        this.elementAt = function (index) {    
            var currentNode = head;    
            var count = 0;    
            while (count < index) {      
                count++;      
                currentNode = currentNode.next;    
            }    
            return currentNode.element;  
        }  
        this.addAt = function (index, element) {    
            var node = new Node(element);    
            var currentNode = head;    
            var previousNode;    
            var currentIndex = 0;    
            if (index > length) {      
                return false;    
            }    
            if (index === 0) {      
                node.next = currentNode;      
                head = node;    
            } else {      
                while (currentIndex < index) {        
                    currentIndex++;        
                    previousNode = currentNode;        
                    currentNode = currentNode.next;      
                }      
                node.next = currentNode;      
                previousNode.next = node;    
            }    
            length++;  
        }  
        this.removeAt = function (index) {    
            var currentNode = head;    
            var previousNode;    
            var currentIndex = 0;    
            if (index < 0 || index >= length) {      
                return null;    
            }    
            if (index === 0) {      
                head = currentIndex.next;    
            } else {      
                while (currentIndex < index) {        
                    currentIndex++;        
                    previousNode = currentNode;        
                    currentNode = currentNode.next;      
                }      
                previousNode.next = currentNode.next;    
            }    
            length--;    
            return currentNode.element;  
        }
    }

4. Set (Tập hợp)

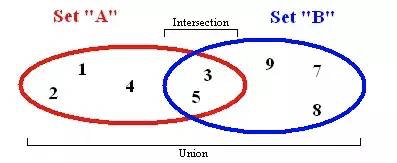
Set (tập hợp) là một khái niệm cơ bản trong toán học: một tập hợp các đối tượng được xác định rõ ràng và khác biệt (không trùng lặp). Được giới thiệu trong ES6, khái niệm tập hợp được giới thiệu có mức độ tương tự với array. Tuy nhiên, một tập hợp không cho phép lặp lại các phần tử và không được lập chỉ mục. Một tập hợp điển hình bao gồm các phương thức sau:

• values: Trả về tất cả các phần tử trong một tập hợp.
• size: Trả về số lượng phần tử trong một tập hợp.
• has: Xác định xem phần tử có tồn tại không.
• add: Chèn các phần tử vào tập hợp.
• remove: Xoá các phần tử trong một tập hợp.
• union: Xác định giao điểm giữa hai tập hợp.
• difference: Trả về sự khác biệt giữa hai tập hợp.
• subset: Xác định xem một tập hợp này có phải là con thuộc tập hợp khác không.

Để phân biệt với khái niệm Set trong ES6, chúng ta định nghĩa MySet trong ví dụ sau:

function MySet() {  
    var collection = [];  
    this.has = function (element) {    
        return (collection.indexOf(element) !== -1);  
    }  
    this.values = function () {    
        return collection;  
    }  
    this.size = function () {    
        return collection.length;  
    }  
    this.add = function (element) {    
        if (!this.has(element)) {      
            collection.push(element);      
            return true;    
        }    
        return false;  
    }  
    this.remove = function (element) {    
        if (this.has(element)) {      
            index = collection.indexOf(element);      
            collection.splice(index, 1);      
            return true;    
        }    
        return false;  
    }  
    this.union = function (otherSet) {    
        var unionSet = new MySet();    
        var firstSet = this.values();    
        var secondSet = otherSet.values();    
        firstSet.forEach(function (e) {      
            unionSet.add(e);    
        });    
        secondSet.forEach(function (e) {      
            unionSet.add(e);    
        });    
        return unionSet;  }  
        this.intersection = function (otherSet) {    
            var intersectionSet = new MySet();    
            var firstSet = this.values();    
            firstSet.forEach(function (e) {      
                if (otherSet.has(e)) {        
                    intersectionSet.add(e);      
                }    
            });    
            return intersectionSet;  
        }  
        this.difference = function (otherSet) {    
            var differenceSet = new MySet();    
            var firstSet = this.values();    
            firstSet.forEach(function (e) {      
                if (!otherSet.has(e)) {        
                    differenceSet.add(e);      
                }    
            });    
            return differenceSet;  
        }  
        this.subset = function (otherSet) {    
            var firstSet = this.values();    
            return firstSet.every(function (value) {      
                return otherSet.has(value);    
            });  
        }
    }

5. Hash Table (Bảng băm)

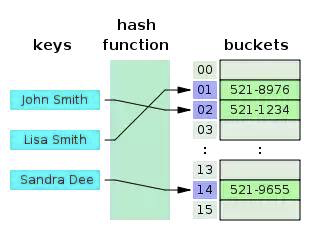
Bảng băm là cấu trúc giữ liệu mà mỗi phần tử trong bảm băm là một cặp key-value (khoá - giá trị). Do việc truy vấn một giá trị thông qua khoá diễn ra nhanh chóng, nó thường được sử dụng trong bản đồ, từ điển hay các cấu trúc dữ liệu đối tượng.

Như hình trên, ta thấy bảng băm sử dụng một hash function (hàm băm) để chuyển đổi các keys thành một dãy số, và các số này đóng vai trò như một giá trị của các các key tương ứng. Bằng cách sử dụng key, ta có thể truy cập các giá trị với một tốc độ rất nhanh với độ phức tạp thời gian có thể đạt tới O(1). Các key giống nhau phải trả về cùng các giá trị - đây là cơ sở của hàm băm.

Bảng băm bao gồm các phương thức sau:

• add: Thêm một cặp key - value (khoá - giá trị).
• remove: Xoá một cặp key - value (khoá - giá trị).
• lookup: Sử dụng khoá để tìm giá trị tương ứng.

Một ví dụ về bảng băm trong Javascript:

function hash(string, max) {
  var hash = 0;
  for (var i = 0; i < string.length; i++) {
    hash += string.charCodeAt(i);
  }
  return hash % max;
}

function HashTable() {
  let storage = [];
  const storageLimit = 4;

  this.add = function (key, value) {
    var index = hash(key, storageLimit);
    if (storage[index] === undefined) {
      storage[index] = [
        [key, value]
      ];
    } else {
      var inserted = false;
      for (var i = 0; i < storage[index].length; i++) {
        if (storage[index][i][0] === key) {
          storage[index][i][1] = value;
          inserted = true;
        }
      }
      if (inserted === false) {
        storage[index].push([key, value]);
      }
    }
  }

  this.remove = function (key) {
    var index = hash(key, storageLimit);
    if (storage[index].length === 1 && storage[index][0][0] === key) {
      delete storage[index];
    } else {
      for (var i = 0; i < storage[index]; i++) {
        if (storage[index][i][0] === key) {
          delete storage[index][i];
        }
      }
    }
  }

  this.lookup = function (key) {
    var index = hash(key, storageLimit);
    if (storage[index] === undefined) {
      return undefined;
    } else {
      for (var i = 0; i < storage[index].length; i++) {
        if (storage[index][i][0] === key) {
          return storage[index][i][1];
        }
      }
    }
  }
}

6. Tree

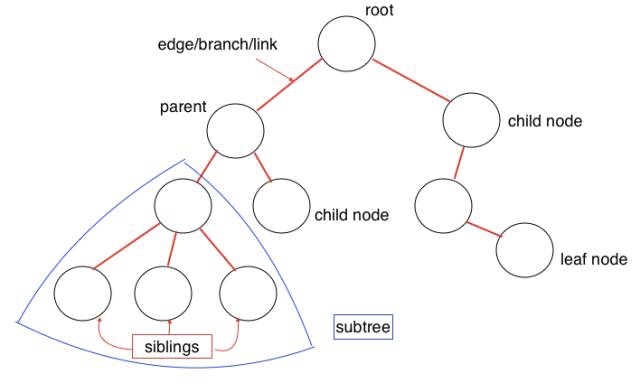
Cấu trúc dữ liệu cây là một dạng cấu trúc nhiều tầng (multi-layer), đồng thời cũng là một dạng cấu trúc dữ liệu phi tuyến tính, so với Array (mảng), Stack (ngăn xếp) và Queue (hàng đợi). Dạng cấu trúc này có hiệu quả cao trong các phép toán thêm và tìm kiếm. Một số khái niệm về cấu trúc dữ liệu dạng cây:

• root: Node gốc của cây, node gốc là node duy nhất không có bất kỳ node cha nào.
• parent node: Node trực tiếp của lớp layer trên, chỉ có một.
• child node: Các node trực tiếp của các lớp layer dưới, có thể có nhiều.
• siblings: Chia sẻ cùng một node cha.
• leaf (Lá): Là node không có bất kỳ node con nào.
• Edge (Cạnh): Liên kết giữa các node.
• Path (Đường): Đoạn dãy tập hợp các cạnh tính từ phần node đầu tiên đến node đích.
• Height of Node (chiều cao của node): Số các cạnh theo đường dài nhất tính từ node đó đến node lá.
• Height of Tree (chiều cao của cây): Số cạnh theo đường dài nhất tính từ node gốc đến node lá.
• Depth of Node (độ sâu của node): Tập hợp số cạnh từ node gốc đến node đang tính.
• Degree of Node: Số lượng các node con.

Dưới đây là ví dụ mô tả một cây tìm kiếm nhị phân. Mỗi node có tối đa hai node với node bên trái nhỏ hơn node hiện tại và node bên phải phải lớn hơn node hiện tại:

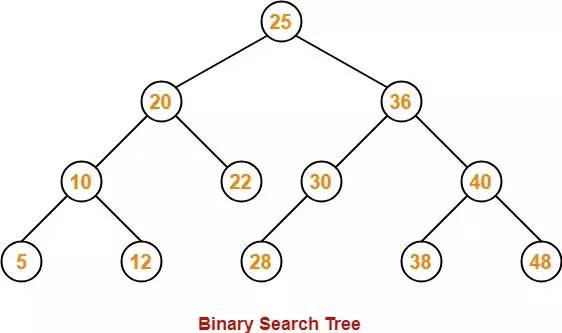
Các phương thức cơ bản của cây tìm kiếm nhị phân (Binary search tree):

• add: Chèn một node vào trong một cây
• findMin: Tìm kiếm node nhỏ nhất.
• findMax: Tìm kiếm node lớn nhất.
• find: Tìm kiếm một phần tử node cụ thể.
• isPresent: Xác định sự tồn tại của một node cụ thể.
• remove: Xoá node khỏi cây.

Ví dụ:

class Node {
  constructor(data, left = null, right = null) {
    this.data = data;
    this.left = left;
    this.right = right;
  }
}

class BST {
  constructor() {
    this.root = null;
  }

  add(data) {
    const node = this.root;
    if (node === null) {
      this.root = new Node(data);
      return;
    } else {
      const searchTree = function (node) {
        if (data < node.data) {
          if (node.left === null) {
            node.left = new Node(data);
            return;
          } else if (node.left !== null) {
            return searchTree(node.left);
          }
        } else if (data > node.data) {
          if (node.right === null) {
            node.right = new Node(data);
            return;
          } else if (node.right !== null) {
            return searchTree(node.right);
          }
        } else {
          return null;
        }
      };
      return searchTree(node);
    }
  }

  findMin() {
    let current = this.root;
    while (current.left !== null) {
      current = current.left;
    }
    return current.data;
  }

  findMax() {
    let current = this.root;
    while (current.right !== null) {
      current = current.right;
    }
    return current.data;
  }

  find(data) {
    let current = this.root;
    while (current.data !== data) {
      if (data < current.data) {
        current = current.left
      } else {
        current = current.right;
      }
      if (current === null) {
        return null;
      }
    }
    return current;
  }

  isPresent(data) {
    let current = this.root;
    while (current) {
      if (data === current.data) {
        return true;
      }
      if (data < current.data) {
        current = current.left;
      } else {
        current = current.right;
      }
    }
    return false;
  }

  remove(data) {
    const removeNode = function (node, data) {
      if (node == null) {
        return null;
      }
      if (data == node.data) {
        // no child node
        if (node.left == null && node.right == null) {
          return null;
        }
        // no left node
        if (node.left == null) {
          return node.right;
        }
        // no right node
        if (node.right == null) {
          return node.left;
        }
        // has 2 child nodes
        var tempNode = node.right;
        while (tempNode.left !== null) {
          tempNode = tempNode.left;
        }
        node.data = tempNode.data;
        node.right = removeNode(node.right, tempNode.data);
        return node;
      } else if (data < node.data) {
        node.left = removeNode(node.left, data);
        return node;
      } else {
        node.right = removeNode(node.right, data);
        return node;
      }
    }
    this.root = removeNode(this.root, data);
  }
}

Kiểm tra:

const bst = new BST();
bst.add(4);
bst.add(2);
bst.add(6);
bst.add(1);
bst.add(3);
bst.add(5);
bst.add(7);
bst.remove(4);
console.log(bst.findMin());
console.log(bst.findMax());
bst.remove(7);
console.log(bst.findMax());
console.log(bst.isPresent(4));

Kết quả:

1
7
6
false

7. Trie

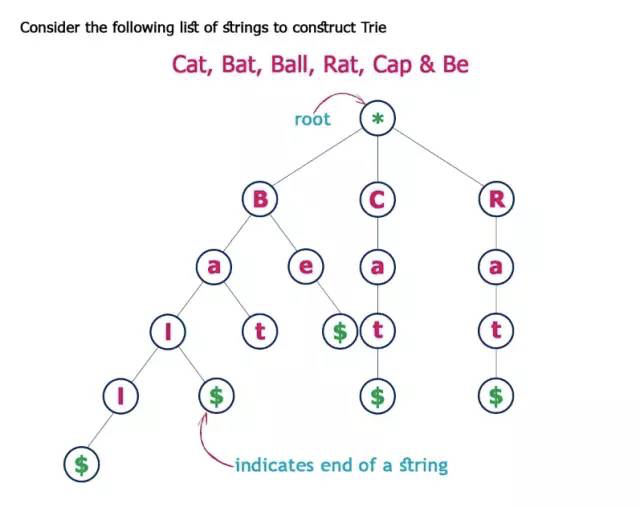
Trie, hay còn gọi là Prefix Tree là một dạng cây tìm kiếm. Trie lưu trữ dữ liệu theo từng bước một (step by step) - mỗi node trong cây đại diện cho một step. Trie được sử dụng trong việc lưu trữ từ vựng, vì vậy nó có thể tìm kiếm nhanh chóng. Mỗi một node trong Trie tương ứng với một chữ cái trong bảng chữ cái - theo nhánh có thể tạo thành một từ hoàn chỉnh.

Các phương thức của Trie bao gồm:

• add: Chèn một từ vào cây từ điển.
• Word: Xác định xem cây hiện tại có đang chứa từ nào đó không.
• print: Trả về tất cả các từ trong cây.

/** Node in Trie **/
function Node() {  
    this.keys = new Map();  
    this.end = false;  
    this.setEnd = function () {    
        this.end = true;  
    };  
    this.isEnd = function () {    
        return this.end;  
    }
}

function Trie() {  
        this.root = new Node();  
        this.add = function (input, node = this.root) {    
            if (input.length === 0) {     
                node.setEnd();      
                return;    
            } else if (!node.keys.has(input[0])) {      
                node.keys.set(input[0], new Node());      
                return this.add(input.substr(1), node.keys.get(input[0]));    
            } else {      
                return this.add(input.substr(1), node.keys.get(input[0]));    
            }  
        }  
        this.isWord = function (word) {    
            let node = this.root;    
            while (word.length > 1) {      
                if (!node.keys.has(word[0])) {        
                    return false;      
                } else {        
                    node = node.keys.get(word[0]);       
                    word = word.substr(1);      
                }    
            }    
            return (node.keys.has(word) && node.keys.get(word).isEnd()) ? true : false;  
        }  
            this.print = function () {    
                let words = new Array();    
                let search = function (node = this.root, string) {      
                    if (node.keys.size != 0) {        
                        for (let letter of node.keys.keys()) {          
                            search(node.keys.get(letter), string.concat(letter));        
                        }        
                        if (node.isEnd()) {          
                            words.push(string);        
                        }      
                    } else {        
                        string.length > 0 ? words.push(string) : undefined;        
                        return;      
                    }    
                };    
                search(this.root, new String());    
                return words.length > 0 ? words : null;  
    }
}

8. Graph (Đồ thị)

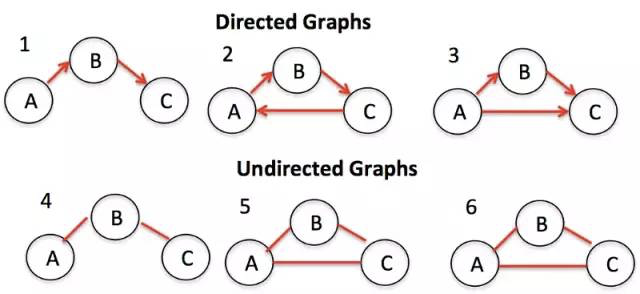
Đồ thị là một tập hợp các node với các liên kết (hoặc cạnh). Nó có thể được chia làm hai nhóm (ví dụ: đồ thị có hướng và đồ thị vô hướng), tuỳ theo việc các liên kết đó có hướng hay không. Graph được sử dụng khá rộng rãi và phổ biến, ví dụ như dùng để tính toán các tuyến đường tốt nhất trong các app về điều hướng, hay gợi ý bạn bè trên các mạng xã hội.

Graph có hai hướng trình bày:

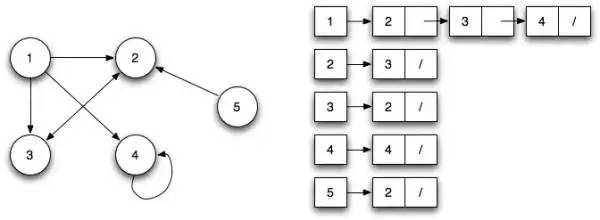
Adjacency List (Danh sách kề):

Đây là danh sách biểu diễn tất cả các cạnh hoặc cung trong một đồ thị. Trong phương pháp này, chúng ta sẽ liệt kê tất cả các node có thể ở bên trái và hiển thị các node kết nối ở bên phải.

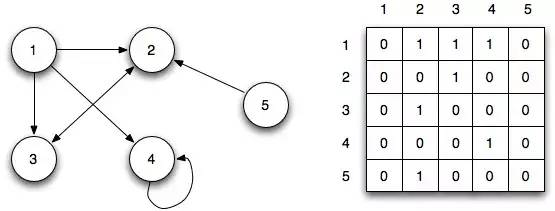
Adjacency Matrix (Ma trận kề):

Ma trận kề sẽ cho hiển thị các node trong hàng và cột, các giao điểm của hàng và cột diễn giải mối quan hệ giữa các node, 0 nghĩa là không được liên kết, 1 nghĩa là liên kết, > 1 nghĩa là có trọng số khác nhau.

Để truy vấn các node trong đồ thị, phải tìm kiếm toàn bộ tree network theo phương pháp Breath-First-Search (BFS) - Tìm kiếm theo chiều rộng và phướng pháp Depth-First-Search (DFS) - tìm kiếm theo chiều sâu.

Ví dụ về BFS trong Javscript:

function bfs(graph, root) {
  var nodesLen = {};
  for (var i = 0; i < graph.length; i++) {
    nodesLen[i] = Infinity;
  }
  nodesLen[root] = 0;
  var queue = [root];
  var current;
  while (queue.length != 0) {
    current = queue.shift();

    var curConnected = graph[current];
    var neighborIdx = [];
    var idx = curConnected.indexOf(1);
    while (idx != -1) {
      neighborIdx.push(idx);
      idx = curConnected.indexOf(1, idx + 1);
    }
    for (var j = 0; j < neighborIdx.length; j++) {
      if (nodesLen[neighborIdx[j]] == Infinity) {
        nodesLen[neighborIdx[j]] = nodesLen[current] + 1;
        queue.push(neighborIdx[j]);
      }
    }
  }
  return nodesLen;
}

Kiểm tra:

var graph = [
  [0, 1, 1, 1, 0],
  [0, 0, 1, 0, 0],
  [1, 1, 0, 0, 0],
  [0, 0, 0, 1, 0],
  [0, 1, 0, 0, 0]
];
console.log(bfs(graph, 1));

Kết quả:

{
  0: 2,
  1: 0,
  2: 1,
  3: 3,
  4: Infinity
}

Trên đây là các loại cấu trúc dữ liệu phổ biến và các ví dụ trong Javascript. Hi vọng các thông tin này sẽ giúp bạn có hình dung tốt hơn về cách thức các cấu trúc dữ liệu hoạt động.

Link bài viết tham khảo tại đây