III. Thuật toán AES - thực hiện (tiếp)
7. MixColumns (tiếp)
Giải đáp bài tập phần trước: Công thức tính phần tử ở cột j j j
S 0 , j ′ = ( 0 x 02 ∗ S 0 , j ) ⊕ ( 0 x 03 ∗ S 1 , j ) ⊕ S 2 , j ⊕ S 3 , j S 1 , j ′ = S 0 , j ⊕ ( 0 x 02 ∗ S 1 , j ) ⊕ ( 0 x 03 ∗ S 2 , j ) ⊕ S 3 , j S 2 , j ′ = S 0 , j ⊕ S 1 , j ⊕ ( 0 x 02 ∗ S 2 , j ) ⊕ ( 0 x 03 ∗ S 3 , j ) S 3 , j ′ = ( 0 x 03 ∗ S 0 , j ) ⊕ S 1 , j ⊕ S 2 , j ⊕ ( 0 x 02 ∗ S 3 , j ) S'_{0,j}=(0x02\ *\ S_{0,j})\oplus (0x03\ *\ S_{1,j})\oplus S_{2,j}\oplus S_{3,j}\\
S'_{1,j}=S_{0,j}\oplus (0x02\ *\ S_{1,j})\oplus (0x03\ *\ S_{2,j})\oplus S_{3,j}\\
S'_{2,j}=S_{0,j}\oplus S_{1,j}\oplus (0x02\ *\ S_{2,j})\oplus (0x03\ *\ S_{3,j})\\
S'_{3,j}=(0x03\ *\ S_{0,j})\oplus S_{1,j}\oplus S_{2,j}\oplus (0x02\ *\ S_{3,j})\\
S 0 , j ′ = ( 0 x 02 ∗ S 0 , j ) ⊕ ( 0 x 03 ∗ S 1 , j ) ⊕ S 2 , j ⊕ S 3 , j S 1 , j ′ = S 0 , j ⊕ ( 0 x 02 ∗ S 1 , j ) ⊕ ( 0 x 03 ∗ S 2 , j ) ⊕ S 3 , j S 2 , j ′ = S 0 , j ⊕ S 1 , j ⊕ ( 0 x 02 ∗ S 2 , j ) ⊕ ( 0 x 03 ∗ S 3 , j ) S 3 , j ′ = ( 0 x 03 ∗ S 0 , j ) ⊕ S 1 , j ⊕ S 2 , j ⊕ ( 0 x 02 ∗ S 3 , j )
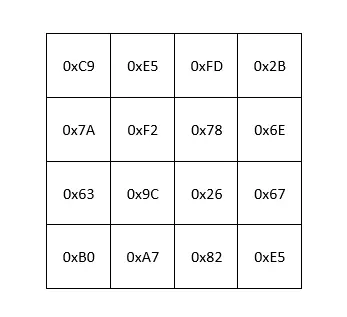
Ví dụ, với state table:
Dựa theo công thức trên chúng ta có:
S 0 , 0 ′ = ( 0 x 02 ∗ S 0 , 0 ) ⊕ ( 0 x 03 ∗ S 1 , 0 ) ⊕ S 2 , 0 ⊕ S 3 , 0 S'_{0,0}=(0x02\ *\ S_{0,0})\oplus (0x03\ *\ S_{1,0})\oplus S_{2,0}\oplus S_{3,0} S 0 , 0 ′ = ( 0 x 02 ∗ S 0 , 0 ) ⊕ ( 0 x 03 ∗ S 1 , 0 ) ⊕ S 2 , 0 ⊕ S 3 , 0 = ( 0 x 02 ∗ 0 x C 9 ) ⊕ ( 0 x 03 ∗ 0 x 7 A ) ⊕ ( 0 x 63 ) ⊕ ( 0 x B 0 ) \ \ \ \ \ \ =(0x02\ *\ 0xC9)\oplus (0x03\ *\ 0x7A)\oplus (0x63)\oplus (0xB0) = ( 0 x 02 ∗ 0 x C 9 ) ⊕ ( 0 x 03 ∗ 0 x 7 A ) ⊕ ( 0 x 63 ) ⊕ ( 0 x B 0 ) = [ ( 0000 0010 ) ∗ ( 1100 1001 ) ] ⊕ [ ( 0000 0011 ) ∗ ( 0111 1010 ) ] ⊕ ( 0110 0011 ) ⊕ ( 1011 0000 ) \ \ \ \ \ \ =[(0000\ 0010)\ *\ (1100\ 1001)]\oplus [(0000\ 0011)\ *\ (0111\ 1010)]\oplus (0110\ 0011)\oplus (1011\ 0000) = [( 0000 0010 ) ∗ ( 1100 1001 )] ⊕ [( 0000 0011 ) ∗ ( 0111 1010 )] ⊕ ( 0110 0011 ) ⊕ ( 1011 0000 ) = [ ( 1001 0010 ) ⊕ ( 0001 1011 ) ] ⊕ { [ ( 0000 0010 ) ∗ ( 0111 1010 ) ] ⊕ ( 0111 1010 ) } ⊕ ( 0110 0011 ) ⊕ ( 1011 0000 ) \ \ \ \ \ \ =[(1001\ 0010)\oplus (0001\ 1011)]\oplus \{[(0000\ 0010)\ *\ (0111\ 1010)]\oplus (0111\ 1010)\}\oplus (0110\ 0011)\oplus (1011\ 0000) = [( 1001 0010 ) ⊕ ( 0001 1011 )] ⊕ {[( 0000 0010 ) ∗ ( 0111 1010 )] ⊕ ( 0111 1010 )} ⊕ ( 0110 0011 ) ⊕ ( 1011 0000 ) = [ ( 1001 0010 ) ⊕ ( 0001 1011 ) ] ⊕ [ ( 111 10100 ) ⊕ ( 0111 1010 ) ] ⊕ ( 0110 0011 ) ⊕ ( 1011 0000 ) \ \ \ \ \ \ =[(1001\ 0010)\oplus (0001\ 1011)]\oplus [(111\ 10100)\oplus (0111\ 1010)]\oplus (0110\ 0011)\oplus (1011\ 0000) = [( 1001 0010 ) ⊕ ( 0001 1011 )] ⊕ [( 111 10100 ) ⊕ ( 0111 1010 )] ⊕ ( 0110 0011 ) ⊕ ( 1011 0000 ) = ( 1000 1001 ) ⊕ ( 1000 1110 ) ⊕ ( 0110 0011 ) ⊕ ( 1011 0000 ) \ \ \ \ \ \ =(1000\ 1001)\oplus (1000\ 1110)\oplus (0110\ 0011)\oplus (1011\ 0000) = ( 1000 1001 ) ⊕ ( 1000 1110 ) ⊕ ( 0110 0011 ) ⊕ ( 1011 0000 ) = ( 0000 0111 ) ⊕ ( 0110 0011 ) ⊕ ( 1011 0000 ) \ \ \ \ \ \ =(0000\ 0111)\oplus (0110\ 0011)\oplus (1011\ 0000) = ( 0000 0111 ) ⊕ ( 0110 0011 ) ⊕ ( 1011 0000 ) = ( 0110 0100 ) ⊕ ( 1011 0000 ) \ \ \ \ \ \ =(0110\ 0100)\oplus (1011\ 0000) = ( 0110 0100 ) ⊕ ( 1011 0000 ) = 1101 0100 \ \ \ \ \ \ =1101\ 0100 = 1101 0100 = 0 x D 4 \ \ \ \ \ \ =0xD4 = 0 x D 4
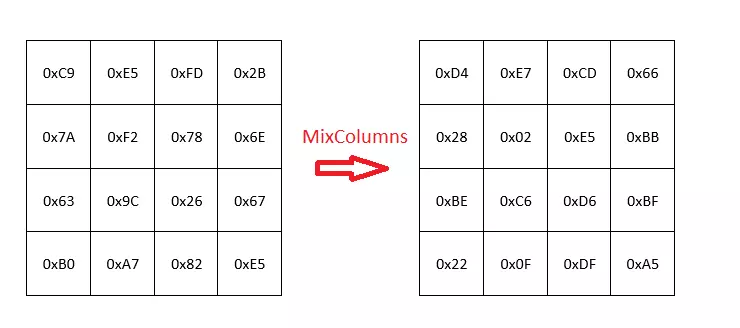
Tương tự chúng ta tính được state table mới:
Tiếp theo chúng ta cùng phân tích cách thực hiện quá trình MixColumns trong lập trình. Đối với phép toán ⊕ \oplus ⊕ ^
( 0000 0010 ) ∗ ( a 7 a 6 a 5 a 4 a 3 a 2 a 1 a 0 ) = { a 6 a 5 a 4 a 3 a 2 a 1 a 0 0 n e ˆ ˊ u a 7 = 0 ( a 6 a 5 a 4 a 3 a 2 a 1 a 0 0 ) ⊕ ( 0001 1011 ) n e ˆ ˊ u a 7 = 1 (0000\ 0010)\ * \ (a_7a_6a_5a_4\ a_3a_2a_1a_0)=
\begin{cases}
a_6a_5a_4a_3\ a_2a_1a_00& \text{nếu }a_7=0\\
(a_6a_5a_4a_3\ a_2a_1a_00)\ \oplus (0001\ 1011)& \text{nếu }a_7=1
\end{cases}
( 0000 0010 ) ∗ ( a 7 a 6 a 5 a 4 a 3 a 2 a 1 a 0 ) = { a 6 a 5 a 4 a 3 a 2 a 1 a 0 0 ( a 6 a 5 a 4 a 3 a 2 a 1 a 0 0 ) ⊕ ( 0001 1011 ) n e ˆ ˊ u a 7 = 0 n e ˆ ˊ u a 7 = 1
Đặt a 7 a 6 a 5 a 4 a 3 a 2 a 1 a 0 = x a_7a_6a_5a_4\ a_3a_2a_1a_0 = x a 7 a 6 a 5 a 4 a 3 a 2 a 1 a 0 = x
a 7 = 0 a_7=0 a 7 = 0 a 7 a_7 a 7 0 0 0 x x x a 7 = 1 a_7=1 a 7 = 1 a 7 a_7 a 7 0 0 0 x x x ⊕ \oplus ⊕ 0001 1011 0001\ 1011 0001 1011 0x1B
(Bạn đọc cần lưu ý giá trị a 6 a 5 a 4 a 3 a 2 a 1 a 0 0 a_6a_5a_4a_3\ a_2a_1a_00 a 6 a 5 a 4 a 3 a 2 a 1 a 0 0 KHÔNG PHẢI là kết quả của phép dịch trái một bit, do dịch trái một bit chúng ta thu được kết quả a 7 a 6 a 5 a 4 a 3 a 2 a 1 a 0 0 a_7\ a_6a_5a_4a_3\ a_2a_1a_00 a 7 a 6 a 5 a 4 a 3 a 2 a 1 a 0 0
Định nghĩa hàm xtime()
def xtime1 ( x) :
if ( x & 0x80 ) :
return ( ( ( x << 1 ) ^ 0x1B ) & 0xFF )
else :
return ( x << 1 )
Kiểm tra điều kiện trường hợp 1 1 1 &0x801000 0000&0xFF1111 11118 8 8 x << 1a 7 = 0 a_7=0 a 7 = 0 a 7 = 0 a_7=0 a 7 = 0
Ngoài ra, do đây là một hàm đơn giản nên các bạn cũng có thể sử dụng hàm nặc danh lambda định nghĩa:
xtime = lambda x: ( ( ( x << 1 ) ^ 0x1B ) & 0xFF ) if ( x & 0x80 ) else ( x << 1 )
Từ đây, phép tính ( 0000 0011 ) ∗ ( a 7 a 6 a 5 a 4 a 3 a 2 a 1 a 0 ) = [ ( 0000 0010 ) ∗ ( a 7 a 6 a 5 a 4 a 3 a 2 a 1 a 0 ) ] ⊕ ( a 7 a 6 a 5 a 4 a 3 a 2 a 1 a 0 ) (0000\ 0011)\ * \ (a_7a_6a_5a_4\ a_3a_2a_1a_0)=[(0000\ 0010)\ * \ (a_7a_6a_5a_4\ a_3a_2a_1a_0) ]\oplus (a_7a_6a_5a_4\ a_3a_2a_1a_0) ( 0000 0011 ) ∗ ( a 7 a 6 a 5 a 4 a 3 a 2 a 1 a 0 ) = [( 0000 0010 ) ∗ ( a 7 a 6 a 5 a 4 a 3 a 2 a 1 a 0 )] ⊕ ( a 7 a 6 a 5 a 4 a 3 a 2 a 1 a 0 ) xtime(x) ^ x
Xét a
S 0 , j ′ = ( 0 x 02 ∗ S 0 , j ) ⊕ ( 0 x 03 ∗ S 1 , j ) ⊕ S 2 , j ⊕ S 3 , j S 1 , j ′ = S 0 , j ⊕ ( 0 x 02 ∗ S 1 , j ) ⊕ ( 0 x 03 ∗ S 2 , j ) ⊕ S 3 , j S 2 , j ′ = S 0 , j ⊕ S 1 , j ⊕ ( 0 x 02 ∗ S 2 , j ) ⊕ ( 0 x 03 ∗ S 3 , j ) S 3 , j ′ = ( 0 x 03 ∗ S 0 , j ) ⊕ S 1 , j ⊕ S 2 , j ⊕ ( 0 x 02 ∗ S 3 , j ) S'_{0,j}=(0x02\ *\ S_{0,j})\oplus (0x03\ *\ S_{1,j})\oplus S_{2,j}\oplus S_{3,j}\\
S'_{1,j}=S_{0,j}\oplus (0x02\ *\ S_{1,j})\oplus (0x03\ *\ S_{2,j})\oplus S_{3,j}\\
S'_{2,j}=S_{0,j}\oplus S_{1,j}\oplus (0x02\ *\ S_{2,j})\oplus (0x03\ *\ S_{3,j})\\
S'_{3,j}=(0x03\ *\ S_{0,j})\oplus S_{1,j}\oplus S_{2,j}\oplus (0x02\ *\ S_{3,j})\\
S 0 , j ′ = ( 0 x 02 ∗ S 0 , j ) ⊕ ( 0 x 03 ∗ S 1 , j ) ⊕ S 2 , j ⊕ S 3 , j S 1 , j ′ = S 0 , j ⊕ ( 0 x 02 ∗ S 1 , j ) ⊕ ( 0 x 03 ∗ S 2 , j ) ⊕ S 3 , j S 2 , j ′ = S 0 , j ⊕ S 1 , j ⊕ ( 0 x 02 ∗ S 2 , j ) ⊕ ( 0 x 03 ∗ S 3 , j ) S 3 , j ′ = ( 0 x 03 ∗ S 0 , j ) ⊕ S 1 , j ⊕ S 2 , j ⊕ ( 0 x 02 ∗ S 3 , j )
Chúng ta có:
a ′ [ 0 ] = xtime ( a [ 0 ] ) ⊕ ( xtime ( a [ 1 ] ) ⊕ a [ 1 ] ) ⊕ a [ 2 ] ⊕ a [ 3 ] a'[0] = \text{xtime}(a[0])\ \oplus\ (\text{xtime}(a[1])\ \oplus\ a[1])\ \oplus\ a[2]\ \oplus\ a[3] a ′ [ 0 ] = xtime ( a [ 0 ]) ⊕ ( xtime ( a [ 1 ]) ⊕ a [ 1 ]) ⊕ a [ 2 ] ⊕ a [ 3 ] a ′ [ 0 ] = ( xtime ( a [ 0 ] ) ⊕ xtime ( a [ 1 ] ) ) ⊕ a [ 1 ] ⊕ a [ 2 ] ⊕ a [ 3 ] a'[0] = (\text{xtime}(a[0])\ \oplus\ \text{xtime}(a[1]))\ \oplus\ a[1]\ \oplus\ a[2]\ \oplus\ a[3] a ′ [ 0 ] = ( xtime ( a [ 0 ]) ⊕ xtime ( a [ 1 ])) ⊕ a [ 1 ] ⊕ a [ 2 ] ⊕ a [ 3 ] a ′ [ 0 ] = xtime ( a [ 0 ] ⊕ a [ 1 ] ) ⊕ a [ 1 ] ⊕ a [ 2 ] ⊕ a [ 3 ] a'[0] = \text{xtime}(a[0]\ \oplus\ a[1])\ \oplus\ a[1]\ \oplus\ a[2]\ \oplus\ a[3] a ′ [ 0 ] = xtime ( a [ 0 ] ⊕ a [ 1 ]) ⊕ a [ 1 ] ⊕ a [ 2 ] ⊕ a [ 3 ] a ′ [ 0 ] = xtime ( a [ 0 ] ⊕ a [ 1 ] ) ⊕ a [ 0 ] ⊕ a [ 0 ] ⊕ a [ 1 ] ⊕ a [ 2 ] ⊕ a [ 3 ] a'[0] = \text{xtime}(a[0]\ \oplus\ a[1])\ \oplus\ a[0]\ \oplus\ a[0]\ \oplus\ a[1]\ \oplus\ a[2]\ \oplus\ a[3] a ′ [ 0 ] = xtime ( a [ 0 ] ⊕ a [ 1 ]) ⊕ a [ 0 ] ⊕ a [ 0 ] ⊕ a [ 1 ] ⊕ a [ 2 ] ⊕ a [ 3 ] a ′ [ 0 ] = xtime ( a [ 0 ] ⊕ a [ 1 ] ) ⊕ a [ 0 ] ⊕ t a'[0] = \text{xtime}(a[0]\ \oplus\ a[1])\ \oplus\ a[0]\ \oplus\ t a ′ [ 0 ] = xtime ( a [ 0 ] ⊕ a [ 1 ]) ⊕ a [ 0 ] ⊕ t
Với t = a [ 0 ] ⊕ a [ 1 ] ⊕ a [ 2 ] ⊕ a [ 3 ] t=a[0]\ \oplus\ a[1]\ \oplus\ a[2]\ \oplus\ a[3] t = a [ 0 ] ⊕ a [ 1 ] ⊕ a [ 2 ] ⊕ a [ 3 ] a[0] ^= t ^ xtime(a[0] ^ a[1])
Tương tự biến đổi như trên, xây dựng được hàm mix_single_column()mix_columns()
def mix_single_column ( a) :
t = a[ 0 ] ^ a[ 1 ] ^ a[ 2 ] ^ a[ 3 ]
u = a[ 0 ]
a[ 0 ] ^ = t ^ xtime( a[ 0 ] ^ a[ 1 ] )
a[ 1 ] ^ = t ^ xtime( a[ 1 ] ^ a[ 2 ] )
a[ 2 ] ^ = t ^ xtime( a[ 2 ] ^ a[ 3 ] )
a[ 3 ] ^ = t ^ xtime( a[ 3 ] ^ u)
def mix_columns ( s) :
for i in range ( 4 ) :
mix_single_column( s[ i] )
Cần sử dụng thêm biến u = a[0]a[3]a[0]
Tiếp theo chúng ta cần giải quyết vấn đề InvMixColumns. Dựa theo quy tắc "nhân" ma trận với các phép toán được quy ước trong GF(2^8), xét các phép tính đặc biệt sau:
S 0 , j = ( 0 x 01 ∗ S 0 , j ) + ( 0 x 00 ∗ S 1 , j ) + ( 0 x 00 ∗ S 2 , j ) + ( 0 x 00 ∗ S 3 , j ) S 1 , j = ( 0 x 00 ∗ S 0 , j ) + ( 0 x 01 ∗ S 1 , j ) + ( 0 x 00 ∗ S 2 , j ) + ( 0 x 00 ∗ S 3 , j ) S 2 , j = ( 0 x 00 ∗ S 0 , j ) + ( 0 x 00 ∗ S 1 , j ) + ( 0 x 01 ∗ S 2 , j ) + ( 0 x 00 ∗ S 3 , j ) S 3 , j = ( 0 x 00 ∗ S 0 , j ) + ( 0 x 00 ∗ S 1 , j ) + ( 0 x 00 ∗ S 2 , j ) + ( 0 x 01 ∗ S 3 , j ) S_{0,j}=(0x01\ *\ S_{0,j})\ +\ (0x00\ *\ S_{1,j})\ +\ (0x00\ *\ S_{2,j})\ +\ (0x00\ *\ S_{3,j})\\
S_{1,j}=(0x00\ *\ S_{0,j})\ +\ (0x01\ *\ S_{1,j})\ +\ (0x00\ *\ S_{2,j})\ +\ (0x00\ *\ S_{3,j})\\
S_{2,j}=(0x00\ *\ S_{0,j})\ +\ (0x00\ *\ S_{1,j})\ +\ (0x01\ *\ S_{2,j})\ +\ (0x00\ *\ S_{3,j})\\
S_{3,j}=(0x00\ *\ S_{0,j})\ +\ (0x00\ *\ S_{1,j})\ +\ (0x00\ *\ S_{2,j})\ +\ (0x01\ *\ S_{3,j})\\
S 0 , j = ( 0 x 01 ∗ S 0 , j ) + ( 0 x 00 ∗ S 1 , j ) + ( 0 x 00 ∗ S 2 , j ) + ( 0 x 00 ∗ S 3 , j ) S 1 , j = ( 0 x 00 ∗ S 0 , j ) + ( 0 x 01 ∗ S 1 , j ) + ( 0 x 00 ∗ S 2 , j ) + ( 0 x 00 ∗ S 3 , j ) S 2 , j = ( 0 x 00 ∗ S 0 , j ) + ( 0 x 00 ∗ S 1 , j ) + ( 0 x 01 ∗ S 2 , j ) + ( 0 x 00 ∗ S 3 , j ) S 3 , j = ( 0 x 00 ∗ S 0 , j ) + ( 0 x 00 ∗ S 1 , j ) + ( 0 x 00 ∗ S 2 , j ) + ( 0 x 01 ∗ S 3 , j )
Biểu diễn dạng ma trận:
[ 0 x 01 0 x 00 0 x 00 0 x 00 0 x 00 0 x 01 0 x 00 0 x 00 0 x 00 0 x 00 0 x 01 0 x 00 0 x 00 0 x 00 0 x 00 0 x 01 ] [ S 0 , 0 S 0 , 1 S 0 , 2 S 0 , 3 S 1 , 0 S 1 , 1 S 1 , 2 S 1 , 3 S 2 , 0 S 2 , 1 S 2 , 2 S 2 , 3 S 3 , 0 S 3 , 1 S 3 , 2 S 3 , 3 ] = [ S 0 , 0 S 0 , 1 S 0 , 2 S 0 , 3 S 1 , 0 S 1 , 1 S 1 , 2 S 1 , 3 S 2 , 0 S 2 , 1 S 2 , 2 S 2 , 3 S 3 , 0 S 3 , 1 S 3 , 2 S 3 , 3 ] \begin{bmatrix}
0x01 & 0x00 & 0x00 & 0x00\\
0x00 & 0x01 & 0x00 & 0x00\\
0x00 & 0x00 & 0x01 & 0x00\\
0x00 & 0x00 & 0x00 & 0x01\\
\end{bmatrix}
\begin{bmatrix}
S_{0,0} & S_{0,1} & S_{0,2} & S_{0,3}\\
S_{1,0} & S_{1,1} & S_{1,2} & S_{1,3}\\
S_{2,0} & S_{2,1} & S_{2,2} & S_{2,3}\\
S_{3,0} & S_{3,1} & S_{3,2} & S_{3,3}\\
\end{bmatrix}
\ =\
\begin{bmatrix}
S_{0,0} & S_{0,1} & S_{0,2} & S_{0,3}\\
S_{1,0} & S_{1,1} & S_{1,2} & S_{1,3}\\
S_{2,0} & S_{2,1} & S_{2,2} & S_{2,3}\\
S_{3,0} & S_{3,1} & S_{3,2} & S_{3,3}\\
\end{bmatrix}
⎣ ⎡ 0 x 01 0 x 00 0 x 00 0 x 00 0 x 00 0 x 01 0 x 00 0 x 00 0 x 00 0 x 00 0 x 01 0 x 00 0 x 00 0 x 00 0 x 00 0 x 01 ⎦ ⎤ ⎣ ⎡ S 0 , 0 S 1 , 0 S 2 , 0 S 3 , 0 S 0 , 1 S 1 , 1 S 2 , 1 S 3 , 1 S 0 , 2 S 1 , 2 S 2 , 2 S 3 , 2 S 0 , 3 S 1 , 3 S 2 , 3 S 3 , 3 ⎦ ⎤ = ⎣ ⎡ S 0 , 0 S 1 , 0 S 2 , 0 S 3 , 0 S 0 , 1 S 1 , 1 S 2 , 1 S 3 , 1 S 0 , 2 S 1 , 2 S 2 , 2 S 3 , 2 S 0 , 3 S 1 , 3 S 2 , 3 S 3 , 3 ⎦ ⎤
Như vậy, nếu ta có thể tìm được một ma trận X X X X :
[ X 0 , 0 X 0 , 1 X 0 , 2 X 0 , 3 X 1 , 0 X 1 , 1 X 1 , 2 X 1 , 3 X 2 , 0 X 2 , 1 X 2 , 2 X 2 , 3 X 3 , 0 X 3 , 1 X 3 , 2 X 3 , 3 ] [ 0 x 02 0 x 03 0 x 01 0 x 01 0 x 01 0 x 02 0 x 03 0 x 01 0 x 01 0 x 01 0 x 02 0 x 03 0 x 03 0 x 01 0 x 01 0 x 02 ] = [ 0 x 01 0 x 00 0 x 00 0 x 00 0 x 00 0 x 01 0 x 00 0 x 00 0 x 00 0 x 00 0 x 01 0 x 00 0 x 00 0 x 00 0 x 00 0 x 01 ] \begin{bmatrix}
X_{0,0} & X_{0,1} & X_{0,2} & X_{0,3}\\
X_{1,0} & X_{1,1} & X_{1,2} & X_{1,3}\\
X_{2,0} & X_{2,1} & X_{2,2} & X_{2,3}\\
X_{3,0} & X_{3,1} & X_{3,2} & X_{3,3}\\
\end{bmatrix}
\begin{bmatrix}
0x02 & 0x03 & 0x01 & 0x01\\
0x01 & 0x02 & 0x03 & 0x01\\
0x01 & 0x01 & 0x02 & 0x03\\
0x03 & 0x01 & 0x01 & 0x02\\
\end{bmatrix}
\ =\
\begin{bmatrix}
0x01 & 0x00 & 0x00 & 0x00\\
0x00 & 0x01 & 0x00 & 0x00\\
0x00 & 0x00 & 0x01 & 0x00\\
0x00 & 0x00 & 0x00 & 0x01\\
\end{bmatrix}
⎣ ⎡ X 0 , 0 X 1 , 0 X 2 , 0 X 3 , 0 X 0 , 1 X 1 , 1 X 2 , 1 X 3 , 1 X 0 , 2 X 1 , 2 X 2 , 2 X 3 , 2 X 0 , 3 X 1 , 3 X 2 , 3 X 3 , 3 ⎦ ⎤ ⎣ ⎡ 0 x 02 0 x 01 0 x 01 0 x 03 0 x 03 0 x 02 0 x 01 0 x 01 0 x 01 0 x 03 0 x 02 0 x 01 0 x 01 0 x 01 0 x 03 0 x 02 ⎦ ⎤ = ⎣ ⎡ 0 x 01 0 x 00 0 x 00 0 x 00 0 x 00 0 x 01 0 x 00 0 x 00 0 x 00 0 x 00 0 x 01 0 x 00 0 x 00 0 x 00 0 x 00 0 x 01 ⎦ ⎤
Thì ta có thể biến đổi:
[ X 0 , 0 X 0 , 1 X 0 , 2 X 0 , 3 X 1 , 0 X 1 , 1 X 1 , 2 X 1 , 3 X 2 , 0 X 2 , 1 X 2 , 2 X 2 , 3 X 3 , 0 X 3 , 1 X 3 , 2 X 3 , 3 ] [ S 0 , 0 ′ S 0 , 1 ′ S 0 , 2 ′ S 0 , 3 ′ S 1 , 0 ′ S 1 , 1 ′ S 1 , 2 ′ S 1 , 3 ′ S 2 , 0 ′ S 2 , 1 ′ S 2 , 2 ′ S 2 , 3 ′ S 3 , 0 ′ S 3 , 1 ′ S 3 , 2 ′ S 3 , 3 ′ ] \begin{bmatrix}
X_{0,0} & X_{0,1} & X_{0,2} & X_{0,3}\\
X_{1,0} & X_{1,1} & X_{1,2} & X_{1,3}\\
X_{2,0} & X_{2,1} & X_{2,2} & X_{2,3}\\
X_{3,0} & X_{3,1} & X_{3,2} & X_{3,3}\\
\end{bmatrix}
\begin{bmatrix}
S'_{0,0} & S'_{0,1} & S'_{0,2} & S'_{0,3}\\
S'_{1,0} & S'_{1,1} & S'_{1,2} & S'_{1,3}\\
S'_{2,0} & S'_{2,1} & S'_{2,2} & S'_{2,3}\\
S'_{3,0} & S'_{3,1} & S'_{3,2} & S'_{3,3}\\
\end{bmatrix}
⎣ ⎡ X 0 , 0 X 1 , 0 X 2 , 0 X 3 , 0 X 0 , 1 X 1 , 1 X 2 , 1 X 3 , 1 X 0 , 2 X 1 , 2 X 2 , 2 X 3 , 2 X 0 , 3 X 1 , 3 X 2 , 3 X 3 , 3 ⎦ ⎤ ⎣ ⎡ S 0 , 0 ′ S 1 , 0 ′ S 2 , 0 ′ S 3 , 0 ′ S 0 , 1 ′ S 1 , 1 ′ S 2 , 1 ′ S 3 , 1 ′ S 0 , 2 ′ S 1 , 2 ′ S 2 , 2 ′ S 3 , 2 ′ S 0 , 3 ′ S 1 , 3 ′ S 2 , 3 ′ S 3 , 3 ′ ⎦ ⎤
= [ X 0 , 0 X 0 , 1 X 0 , 2 X 0 , 3 X 1 , 0 X 1 , 1 X 1 , 2 X 1 , 3 X 2 , 0 X 2 , 1 X 2 , 2 X 2 , 3 X 3 , 0 X 3 , 1 X 3 , 2 X 3 , 3 ] [ 0 x 02 0 x 03 0 x 01 0 x 01 0 x 01 0 x 02 0 x 03 0 x 01 0 x 01 0 x 01 0 x 02 0 x 03 0 x 03 0 x 01 0 x 01 0 x 02 ] [ S 0 , 0 S 0 , 1 S 0 , 2 S 0 , 3 S 1 , 0 S 1 , 1 S 1 , 2 S 1 , 3 S 2 , 0 S 2 , 1 S 2 , 2 S 2 , 3 S 3 , 0 S 3 , 1 S 3 , 2 S 3 , 3 ] \ =
\begin{bmatrix}
X_{0,0} & X_{0,1} & X_{0,2} & X_{0,3}\\
X_{1,0} & X_{1,1} & X_{1,2} & X_{1,3}\\
X_{2,0} & X_{2,1} & X_{2,2} & X_{2,3}\\
X_{3,0} & X_{3,1} & X_{3,2} & X_{3,3}\\
\end{bmatrix}
\begin{bmatrix}
0x02 & 0x03 & 0x01 & 0x01\\
0x01 & 0x02 & 0x03 & 0x01\\
0x01 & 0x01 & 0x02 & 0x03\\
0x03 & 0x01 & 0x01 & 0x02\\
\end{bmatrix}
\begin{bmatrix}
S_{0,0} & S_{0,1} & S_{0,2} & S_{0,3}\\
S_{1,0} & S_{1,1} & S_{1,2} & S_{1,3}\\
S_{2,0} & S_{2,1} & S_{2,2} & S_{2,3}\\
S_{3,0} & S_{3,1} & S_{3,2} & S_{3,3}\\
\end{bmatrix}
= ⎣ ⎡ X 0 , 0 X 1 , 0 X 2 , 0 X 3 , 0 X 0 , 1 X 1 , 1 X 2 , 1 X 3 , 1 X 0 , 2 X 1 , 2 X 2 , 2 X 3 , 2 X 0 , 3 X 1 , 3 X 2 , 3 X 3 , 3 ⎦ ⎤ ⎣ ⎡ 0 x 02 0 x 01 0 x 01 0 x 03 0 x 03 0 x 02 0 x 01 0 x 01 0 x 01 0 x 03 0 x 02 0 x 01 0 x 01 0 x 01 0 x 03 0 x 02 ⎦ ⎤ ⎣ ⎡ S 0 , 0 S 1 , 0 S 2 , 0 S 3 , 0 S 0 , 1 S 1 , 1 S 2 , 1 S 3 , 1 S 0 , 2 S 1 , 2 S 2 , 2 S 3 , 2 S 0 , 3 S 1 , 3 S 2 , 3 S 3 , 3 ⎦ ⎤
= [ 0 x 01 0 x 00 0 x 00 0 x 00 0 x 00 0 x 01 0 x 00 0 x 00 0 x 00 0 x 00 0 x 01 0 x 00 0 x 00 0 x 00 0 x 00 0 x 01 ] [ S 0 , 0 S 0 , 1 S 0 , 2 S 0 , 3 S 1 , 0 S 1 , 1 S 1 , 2 S 1 , 3 S 2 , 0 S 2 , 1 S 2 , 2 S 2 , 3 S 3 , 0 S 3 , 1 S 3 , 2 S 3 , 3 ] = [ S 0 , 0 S 0 , 1 S 0 , 2 S 0 , 3 S 1 , 0 S 1 , 1 S 1 , 2 S 1 , 3 S 2 , 0 S 2 , 1 S 2 , 2 S 2 , 3 S 3 , 0 S 3 , 1 S 3 , 2 S 3 , 3 ] \ =
\begin{bmatrix}
0x01 & 0x00 & 0x00 & 0x00\\
0x00 & 0x01 & 0x00 & 0x00\\
0x00 & 0x00 & 0x01 & 0x00\\
0x00 & 0x00 & 0x00 & 0x01\\
\end{bmatrix}
\begin{bmatrix}
S_{0,0} & S_{0,1} & S_{0,2} & S_{0,3}\\
S_{1,0} & S_{1,1} & S_{1,2} & S_{1,3}\\
S_{2,0} & S_{2,1} & S_{2,2} & S_{2,3}\\
S_{3,0} & S_{3,1} & S_{3,2} & S_{3,3}\\
\end{bmatrix}
\ =
\begin{bmatrix}
S_{0,0} & S_{0,1} & S_{0,2} & S_{0,3}\\
S_{1,0} & S_{1,1} & S_{1,2} & S_{1,3}\\
S_{2,0} & S_{2,1} & S_{2,2} & S_{2,3}\\
S_{3,0} & S_{3,1} & S_{3,2} & S_{3,3}\\
\end{bmatrix}
= ⎣ ⎡ 0 x 01 0 x 00 0 x 00 0 x 00 0 x 00 0 x 01 0 x 00 0 x 00 0 x 00 0 x 00 0 x 01 0 x 00 0 x 00 0 x 00 0 x 00 0 x 01 ⎦ ⎤ ⎣ ⎡ S 0 , 0 S 1 , 0 S 2 , 0 S 3 , 0 S 0 , 1 S 1 , 1 S 2 , 1 S 3 , 1 S 0 , 2 S 1 , 2 S 2 , 2 S 3 , 2 S 0 , 3 S 1 , 3 S 2 , 3 S 3 , 3 ⎦ ⎤ = ⎣ ⎡ S 0 , 0 S 1 , 0 S 2 , 0 S 3 , 0 S 0 , 1 S 1 , 1 S 2 , 1 S 3 , 1 S 0 , 2 S 1 , 2 S 2 , 2 S 3 , 2 S 0 , 3 S 1 , 3 S 2 , 3 S 3 , 3 ⎦ ⎤
Giải phương trình ma trận X chúng ta thu được kết quả:
[ 0 x 0 E 0 x 0 B 0 x 0 D 0 x 09 0 x 09 0 x 0 E 0 x 0 B 0 x 0 D 0 x 0 D 0 x 09 0 x 0 E 0 x 0 B 0 x 0 B 0 x 0 D 0 x 09 0 x 0 E ] \begin{bmatrix}
0x0E & 0x0B & 0x0D & 0x09\\
0x09 & 0x0E & 0x0B & 0x0D\\
0x0D & 0x09 & 0x0E & 0x0B\\
0x0B & 0x0D & 0x09 & 0x0E\\
\end{bmatrix}
⎣ ⎡ 0 x 0 E 0 x 09 0 x 0 D 0 x 0 B 0 x 0 B 0 x 0 E 0 x 09 0 x 0 D 0 x 0 D 0 x 0 B 0 x 0 E 0 x 09 0 x 09 0 x 0 D 0 x 0 B 0 x 0 E ⎦ ⎤
Do thực hiện phép tính với ma trận X X X
[ 0 x 0 E 0 x 0 B 0 x 0 D 0 x 09 0 x 09 0 x 0 E 0 x 0 B 0 x 0 D 0 x 0 D 0 x 09 0 x 0 E 0 x 0 B 0 x 0 B 0 x 0 D 0 x 09 0 x 0 E ] = [ 0 x 02 0 x 03 0 x 01 0 x 01 0 x 01 0 x 02 0 x 03 0 x 01 0 x 01 0 x 01 0 x 02 0 x 03 0 x 03 0 x 01 0 x 01 0 x 02 ] [ 0 x 05 0 x 00 0 x 04 0 x 00 0 x 00 0 x 05 0 x 00 0 x 04 0 x 04 0 x 00 0 x 05 0 x 00 0 x 00 0 x 04 0 x 00 0 x 05 ] \begin{bmatrix}
0x0E & 0x0B & 0x0D & 0x09\\
0x09 & 0x0E & 0x0B & 0x0D\\
0x0D & 0x09 & 0x0E & 0x0B\\
0x0B & 0x0D & 0x09 & 0x0E\\
\end{bmatrix}
\ =
\begin{bmatrix}
0x02 & 0x03 & 0x01 & 0x01\\
0x01 & 0x02 & 0x03 & 0x01\\
0x01 & 0x01 & 0x02 & 0x03\\
0x03 & 0x01 & 0x01 & 0x02\\
\end{bmatrix}
\begin{bmatrix}
0x05 & 0x00 & 0x04 & 0x00\\
0x00 & 0x05 & 0x00 & 0x04\\
0x04 & 0x00 & 0x05 & 0x00\\
0x00 & 0x04 & 0x00 & 0x05\\
\end{bmatrix}
⎣ ⎡ 0 x 0 E 0 x 09 0 x 0 D 0 x 0 B 0 x 0 B 0 x 0 E 0 x 09 0 x 0 D 0 x 0 D 0 x 0 B 0 x 0 E 0 x 09 0 x 09 0 x 0 D 0 x 0 B 0 x 0 E ⎦ ⎤ = ⎣ ⎡ 0 x 02 0 x 01 0 x 01 0 x 03 0 x 03 0 x 02 0 x 01 0 x 01 0 x 01 0 x 03 0 x 02 0 x 01 0 x 01 0 x 01 0 x 03 0 x 02 ⎦ ⎤ ⎣ ⎡ 0 x 05 0 x 00 0 x 04 0 x 00 0 x 00 0 x 05 0 x 00 0 x 04 0 x 04 0 x 00 0 x 05 0 x 00 0 x 00 0 x 04 0 x 00 0 x 05 ⎦ ⎤
Như vậy, công việc trở nên đơn giản hơn là lập trình phép tính ma trận dưới, sau đó thực hiện hàm MixColumns trước đó:
[ 0 x 05 0 x 00 0 x 04 0 x 00 0 x 00 0 x 05 0 x 00 0 x 04 0 x 04 0 x 00 0 x 05 0 x 00 0 x 00 0 x 04 0 x 00 0 x 05 ] [ S 0 , 0 ′ S 0 , 1 ′ S 0 , 2 ′ S 0 , 3 ′ S 1 , 0 ′ S 1 , 1 ′ S 1 , 2 ′ S 1 , 3 ′ S 2 , 0 ′ S 2 , 1 ′ S 2 , 2 ′ S 2 , 3 ′ S 3 , 0 ′ S 3 , 1 ′ S 3 , 2 ′ S 3 , 3 ′ ] \begin{bmatrix}
0x05 & 0x00 & 0x04 & 0x00\\
0x00 & 0x05 & 0x00 & 0x04\\
0x04 & 0x00 & 0x05 & 0x00\\
0x00 & 0x04 & 0x00 & 0x05\\
\end{bmatrix}
\begin{bmatrix}
S'_{0,0} & S'_{0,1} & S'_{0,2} & S'_{0,3}\\
S'_{1,0} & S'_{1,1} & S'_{1,2} & S'_{1,3}\\
S'_{2,0} & S'_{2,1} & S'_{2,2} & S'_{2,3}\\
S'_{3,0} & S'_{3,1} & S'_{3,2} & S'_{3,3}\\
\end{bmatrix}
⎣ ⎡ 0 x 05 0 x 00 0 x 04 0 x 00 0 x 00 0 x 05 0 x 00 0 x 04 0 x 04 0 x 00 0 x 05 0 x 00 0 x 00 0 x 04 0 x 00 0 x 05 ⎦ ⎤ ⎣ ⎡ S 0 , 0 ′ S 1 , 0 ′ S 2 , 0 ′ S 3 , 0 ′ S 0 , 1 ′ S 1 , 1 ′ S 2 , 1 ′ S 3 , 1 ′ S 0 , 2 ′ S 1 , 2 ′ S 2 , 2 ′ S 3 , 2 ′ S 0 , 3 ′ S 1 , 3 ′ S 2 , 3 ′ S 3 , 3 ′ ⎦ ⎤
Bạn đọc có thể tham khảo hàm inv_mix_columns()https://cs.ru.nl/~joan/papers/JDA_VRI_Rijndael_2002.pdf mục 4.1.3 4.1.3 4.1.3
def inv_mix_columns ( s) :
for i in range ( 4 ) :
u = xtime( xtime( s[ i] [ 0 ] ^ s[ i] [ 2 ] ) )
v = xtime( xtime( s[ i] [ 1 ] ^ s[ i] [ 3 ] ) )
s[ i] [ 0 ] ^ = u
s[ i] [ 1 ] ^ = v
s[ i] [ 2 ] ^ = u
s[ i] [ 3 ] ^ = v
mix_columns( s)
Tài liệu tham khảo