Stack trong Python

Stack là một cấu trúc dữ liệu tuân theo nguyên tắc LIFO (Last In, First Out), nghĩa là phần tử được thêm vào cuối cùng sẽ được lấy ra đầu tiên.

Giả sử ta có 4 cuốn sách và sắp xếp nó thành một stack:

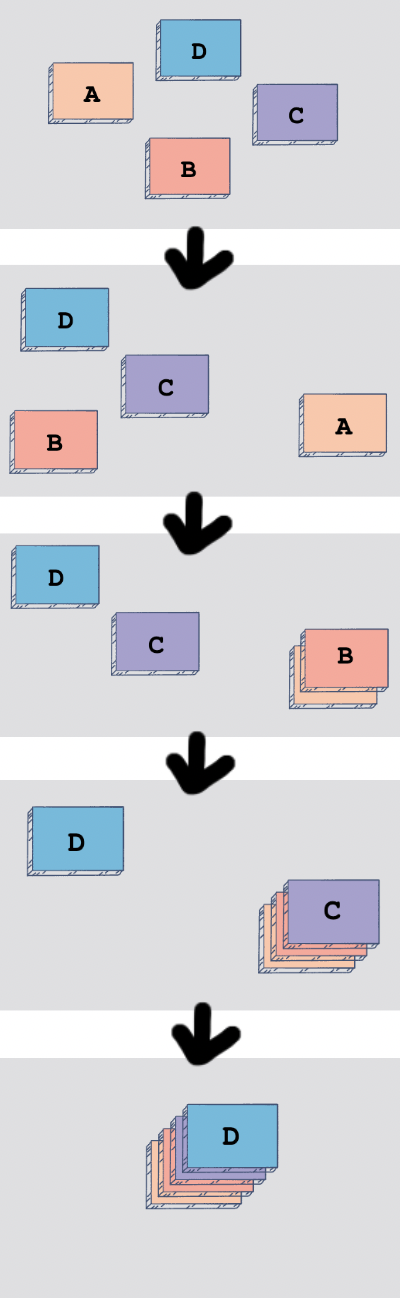
Ví dụ, nếu anh muốn lấy Book A và nó đang nằm ở dưới đáy của chồng sách, anh sẽ phải lần lượt lấy Book D, rồi Book C, và Book B xuống trước, rồi mới có thể lấy được Book A.

Stack trong lập trình hoạt động rất giống với chồng sách mà ta thấy ở trên. Stack là một cấu trúc dữ liệu cho phép ta "đặt" (push) bất kỳ đối tượng, biến hoặc giá trị nào lên trên cùng, giống như cách ta đặt sách lên chồng. Khi ta muốn "lấy" (pop) một giá trị, ta sẽ lấy giá trị ở trên cùng trước, tương tự như lấy cuốn sách trên cùng của chồng sách.

Các thao tác cơ bản trên stack

• Push: Thêm một phần tử vào đỉnh (top) của stack.
• Pop: Xóa và trả về phần tử ở đỉnh của stack.
• Peek: Trả về phần tử ở đỉnh của stack mà không xóa nó.
• isEmpty: Kiểm tra xem stack có rỗng hay không.
• isFull: Kiểm tra xem stack có đầy không (nếu stack có giới hạn kích thước).

Giờ chúng ta sẽ tạo class Stack:

"""
Stack Data Structure.
"""
class Stack:
    def __init__(self):
        # Khởi tạo stack như một danh sách trống
        self.stack = []

    def push(self, item):
        # Thêm một phần tử vào đỉnh của stack
        self.stack.append(item)

    def pop(self):
        # Xóa và trả về phần tử ở đỉnh của stack
        # Kiểm tra xem stack có rỗng không để tránh lỗi
        if not self.is_empty():
            return self.stack.pop()
        else:
            return "Stack is empty, cannot pop."

    def peek(self):
        # Trả về phần tử ở đỉnh của stack mà không xóa nó
        # Kiểm tra xem stack có rỗng không để tránh lỗi
        if not self.is_empty():
            return self.stack[-1]
        else:
            return "Stack is empty, no top element to peek."

    def is_empty(self):
        # Kiểm tra xem stack có rỗng không
        return len(self.stack) == 0

    def size(self):
        # Trả về số lượng phần tử trong stack
        return len(self.stack)

    def __str__(self):
        # Trả về nội dung của stack dưới dạng chuỗi để dễ quan sát
        return str(self.stack)

# Sử dụng lớp Stack
stack = Stack()

# Thêm các phần tử vào stack
stack.push(10)
stack.push(20)
stack.push(30)

print("Stack sau khi push các phần tử:", stack) # Output: Stack sau khi push các phần tử: [10, 20, 30]

# Xem phần tử ở đỉnh của stack
print("Phần tử ở đỉnh của stack (peek):", stack.peek()) # Output: Phần tử ở đỉnh của stack (peek): 30

# Xóa phần tử ở đỉnh của stack
print("Phần tử được lấy ra từ stack (pop):", stack.pop()) # Output: Phần tử được lấy ra từ stack (pop): 30
print("Stack sau khi pop:", stack) # Output: Stack sau khi pop: [10, 20]

# Kiểm tra xem stack có rỗng không
print("Stack có rỗng không?", stack.is_empty()) # Output: Stack có rỗng không? False

# Trả về kích thước của stack
print("Kích thước của stack:", stack.size()) # Output: Kích thước của stack: 2

Determine if Brackets are Balanced

Cho một chuỗi chứa các dấu ngoặc (), {}, []. Nhiệm vụ của chúng ta là viết một hàm để kiểm tra xem các dấu ngoặc này có được sắp xếp hợp lệ hay không.

Ví dụ về Balanced Brackets

• { }
• { } { }
• ( ( { [ ] } ) )

Ví dụ về Unbalanced Brackets

• ( ( )
• { { { ) } ]
• [ ] [ ] ] ]

Cách tiếp cận

• Sử dụng một stack để lưu trữ các dấu mở ngoặc.
• Duyệt qua từng ký tự trong chuỗi:
  • Nếu gặp dấu mở ngoặc ((, {, [), thì đẩy nó vào stack.
  • Nếu gặp dấu đóng ngoặc (), }, ]):
    • Kiểm tra xem stack có rỗng không (nếu rỗng nghĩa là chuỗi không cân bằng).
    • Lấy phần tử trên cùng của stack ra và kiểm tra xem nó có tương ứng với dấu đóng hiện tại không. Nếu không, chuỗi không cân bằng.
• Cuối cùng, nếu stack rỗng thì chuỗi cân bằng, nếu không rỗng thì chuỗi không cân bằng.

stack.py

"""
Stack Data Structure.
"""
class Stack():
    def __init__(self):
        self.items = []

    def push(self, item):
        self.items.append(item)

    def pop(self):
        return self.items.pop()

    def is_empty(self):
        return self.items == []

    def peek(self):
        if not self.is_empty():
            return self.items[-1]

    def get_stack(self):
        return self.items

main.py

from stack import Stack

def is_match(p1, p2):
    if p1 == "(" and p2 == ")":
        return True
    elif p1 == "{" and p2 == "}":
        return True
    elif p1 == "[" and p2 == "]":
        return True
    else:
        return False


def is_paren_balanced(paren_string):
    s = Stack()
    is_balanced = True
    index = 0

    while index < len(paren_string) and is_balanced:
        paren = paren_string[index]
        if paren in "([{":
            s.push(paren)
        else:
            if s.is_empty():
                is_balanced = False
                break
            else:
                top = s.pop()
                if not is_match(top, paren):
                    is_balanced = False
                    break
        index += 1

    if s.is_empty() and is_balanced:
        return True
    else:
        return False

print("String : (((({})))) Balanced or not?")
print(is_paren_balanced("(((({}))))")) # Output: True


print("String : [][]]] Balanced or not?")
print(is_paren_balanced("[][]]]")) # Output: False

print("String : [][] Balanced or not?")
print(is_paren_balanced("[][]")) # Output: True

Giải thích hàm is_paren_balanced(paren_string)

Chúng ta khai báo một Stack s (ban đầu là rỗng), và hai biến is_balanced và index được gán giá trị lần lượt là True và 0.

is_balanced sẽ được sử dụng để theo dõi trạng thái cân bằng của các dấu ngoặc, và index sẽ dùng để duyệt qua các ký tự trong chuỗi paren_string.

Vòng lặp while chạy cho đến khi chúng ta đã duyệt qua toàn bộ chuỗi hoặc cho đến khi phát hiện rằng chuỗi không cân bằng (is_balanced trở thành False).

Vòng lặp này duyệt qua từng ký tự trong chuỗi paren_string bằng cách sử dụng biến index. Ký tự hiện tại sẽ được lưu trong biến paren.

Tiếp theo, chương trình kiểm tra xem ký tự hiện tại (paren) có phải là một trong các dấu ngoặc mở ((, {, [) không. Nếu đúng, dấu ngoặc mở được đẩy vào stack s bằng thao tác s.push(paren).

Nếu ký tự không phải là dấu ngoặc mở:

• Kiểm tra xem stack s có rỗng không. Nếu stack rỗng, điều này có nghĩa là có một dấu ngoặc đóng mà không có dấu ngoặc mở tương ứng, do đó chuỗi không cân bằng (is_balanced = False), và chúng ta thoát khỏi vòng lặp (break).
• Nếu stack không rỗng:
  • Chúng ta lấy phần tử trên cùng của stack (top = s.pop()) và kiểm tra xem nó có khớp với dấu ngoặc đóng hiện tại hay không bằng cách sử dụng hàm is_match.
  • Nếu dấu ngoặc mở ở đỉnh của stack không khớp với dấu ngoặc đóng hiện tại, chuỗi không cân bằng (is_balanced = False), và chúng ta thoát khỏi vòng lặp (break).

Tiếp theo, tăng giá trị index để tiếp tục duyệt qua ký tự tiếp theo trong chuỗi.

Sau khi vòng lặp while kết thúc, chúng ta kiểm tra xem stack có rỗng và biến is_balanced có vẫn là True không.

• Nếu cả hai điều kiện đều đúng, điều đó có nghĩa là chuỗi có các dấu ngoặc cân bằng hoàn toàn, và hàm sẽ trả về True.

Nếu stack không rỗng hoặc biến is_balanced là False, điều này có nghĩa là chuỗi không cân bằng, và hàm sẽ trả về False.

Giải thích hàm is_match(p1, p2)

Hàm is_match được sử dụng để kiểm tra xem hai ký tự, cụ thể là p1 và p2, có phải là một cặp dấu ngoặc hợp lệ hay không. Để p1 và p2 khớp nhau:

• p1 phải là một dấu ngoặc mở ((, {, [).
• p2 phải là dấu ngoặc đóng tương ứng (), }, ]).

Nếu p1 và p2 khớp nhau theo đúng điều kiện trên, hàm sẽ trả về True. Nếu không, hàm sẽ trả về False.

Reverse String

Thuật toán để đảo ngược một chuỗi bằng cách sử dụng stack là khá đơn giản và hiệu quả. Thuật toán này hoạt động dựa trên tính chất LIFO (Last-In, First-Out) của stack, nghĩa là phần tử được đưa vào sau cùng sẽ được lấy ra đầu tiên. Khi chúng ta đẩy tất cả các ký tự của chuỗi vào stack, và sau đó lấy chúng ra theo thứ tự ngược lại, chúng ta sẽ thu được một chuỗi đã được đảo ngược.

• Bằng cách duyệt qua từng ký tự trong chuỗi và đẩy nó vào stack, chúng ta lưu trữ các ký tự theo thứ tự ngược lại trong stack.
• Khi chúng ta lần lượt lấy từng ký tự ra từ stack, ký tự đầu tiên được đẩy vào sẽ là ký tự cuối cùng được lấy ra, giúp tạo ra chuỗi đảo ngược.

main.py

from stack import Stack
def reverse_string(stack, input_str):

    for i in range(len(input_str)):
        stack.push(input_str[i])

    rev_str = ""

    while not stack.is_empty():
        rev_str += stack.pop()

    return rev_str

stack = Stack()
input_str = "!olbiV ot emocleW"
print(reverse_string(stack, input_str)) # Output: Welcome to Viblo!

• Vòng lặp for này lặp qua từng ký tự trong chuỗi input_str bằng cách sử dụng index i.
• Mỗi ký tự từ input_str[i] được đưa vào stack thông qua phương thức stack.push(input_str[i]).
• Kết quả là tất cả các ký tự của input_str được đẩy vào stack theo thứ tự từ đầu đến cuối.
• Biến rev_str được khởi tạo là một chuỗi trống ("").
• Biến này sẽ được sử dụng để xây dựng chuỗi đã được đảo ngược.
• Vòng lặp while này tiếp tục chạy miễn là stack không rỗng (not stack.is_empty()).
• Trong mỗi lần lặp, phần tử trên cùng của stack được lấy ra bằng phương thức stack.pop() và được nối thêm vào chuỗi rev_str.
• Vì stack là cấu trúc dữ liệu LIFO (Last-In, First-Out), các ký tự được đưa vào sau cùng sẽ được lấy ra trước, do đó rev_str sẽ chứa các ký tự theo thứ tự ngược lại so với chuỗi ban đầu.
• Sau khi vòng lặp while kết thúc (nghĩa là stack đã rỗng), chuỗi rev_str sẽ chứa phiên bản đảo ngược của input_str.
• Hàm reverse_string trả về chuỗi rev_str này.

Convert Decimal Integer to Binary

main.py

from stack import Stack

def convert_int_to_bin(dec_num):

    if dec_num == 0:
        return 0

    s = Stack()

    while dec_num > 0:
        remainder = dec_num % 2
        s.push(remainder)
        dec_num = dec_num // 2

    bin_num = ""
    while not s.is_empty():
        bin_num += str(s.pop())

    return bin_num

print(convert_int_to_bin(56)) # Output: 111000
print(convert_int_to_bin(2)) # Output: 10
print(convert_int_to_bin(32)) # Output: 100000
print(convert_int_to_bin(10)) # Output: 1010
print(int(convert_int_to_bin(56),2)==56) # Output: True

Hàm này chuyển đổi một số nguyên thập phân (dec_num) sang dạng nhị phân bằng cách chia liên tục số đó cho 2 và lưu trữ phần dư vào stack. Sau khi quá trình chia hoàn tất, các phần dư sẽ được lấy ra từ stack để tạo thành số nhị phân.

• Hàm bắt đầu bằng việc kiểm tra nếu dec_num bằng 0, hàm sẽ trả về 0.

• Một đối tượng stack s được khởi tạo. Stack này sẽ được sử dụng để lưu trữ các phần dư khi thực hiện phép chia.

• Vòng lặp while chạy cho đến khi dec_num lớn hơn 0. Ở mỗi vòng lặp:

  • remainder = dec_num % 2: Tính phần dư của dec_num khi chia cho 2. Phần dư này sẽ là một trong các chữ số trong biểu diễn nhị phân.
  • s.push(remainder): Phần dư được đẩy vào stack.
  • dec_num = dec_num // 2: Cập nhật giá trị dec_num bằng thương của phép chia dec_num cho 2.

• Phần dư của mỗi phép chia biểu diễn các bit nhị phân từ phải sang trái, vì vậy các bit này được đẩy vào stack để sau này có thể lấy ra theo thứ tự ngược lại.

• Sau khi đã đẩy tất cả các phần dư vào stack, hàm tạo một chuỗi trống bin_num để lưu trữ số nhị phân.

• Vòng lặp while tiếp tục chạy cho đến khi stack rỗng (s.is_empty() trả về True):

  • bin_num += str(s.pop()): Mỗi lần lặp, phần tử trên cùng của stack (là một chữ số nhị phân) được lấy ra và nối vào chuỗi bin_num.
  • Vì các phần tử được đẩy vào stack từ phải sang trái, nên khi lấy ra từ stack, chúng sẽ được xếp đúng thứ tự để tạo thành số nhị phân.

• Cuối cùng, hàm trả về chuỗi nhị phân bin_num, là kết quả của quá trình chuyển đổi từ số nguyên thập phân ban đầu.

Ví dụ Nếu dec_num = 10, thì:

• 10 chia 2 dư 0 (push 0 vào stack)
• 5 chia 2 dư 1 (push 1 vào stack)
• 2 chia 2 dư 0 (push 0 vào stack)
• 1 chia 2 dư 1 (push 1 vào stack)

Stack sẽ chứa [0, 1, 0, 1]. Sau khi pop từ stack và nối lại, chuỗi kết quả sẽ là "1010", tức là dạng nhị phân của 10.

Bài viết nằm trong series Data Structures và Algorithms trong Python