So sánh các thuật toán sắp xếp

Tại sao chúng ta cần nghiên cứu, thiết kế phân tích các thuật toán sắp xếp? Dưới đây là một số lý do quan trọng:

• Chúng ta có thể học một số cách tiếp cận giải quyết vấn đề bằng cách sử dụng các thuật toán sắp xếp: cách tiếp cận tăng dần (insertion sort và selection sort), chia để trị (merge sort và quicksort), cách tiếp cận hai con trỏ (merge sort và heapsort ), giải quyết vấn đề bằng cách sử dụng cấu trúc dữ liệu (heapsort và tree sort),...
• Đây là một trong những ý tưởng tốt nhất để hiểu phân tích độ phức tạp của code đệ quy và lặp lại.
• Chúng ta cũng sử dụng sắp xếp như một cách tiếp cận giải quyết vấn đề, tức là chúng ta có thể giải quyết một số vấn đề một cách hiệu quả bằng cách sắp xếp dữ liệu theo thứ tự.

Bài viết này sẽ phân tích và so sánh các thuật toán sắp xếp khác nhau dựa trên các tham số khác nhau như độ phức tạp về thời gian, độ phức tạp về không gian, độ ổn định, trực tuyến so với ngoại tuyến, cách tiếp cận giải quyết vấn đề, v.v.

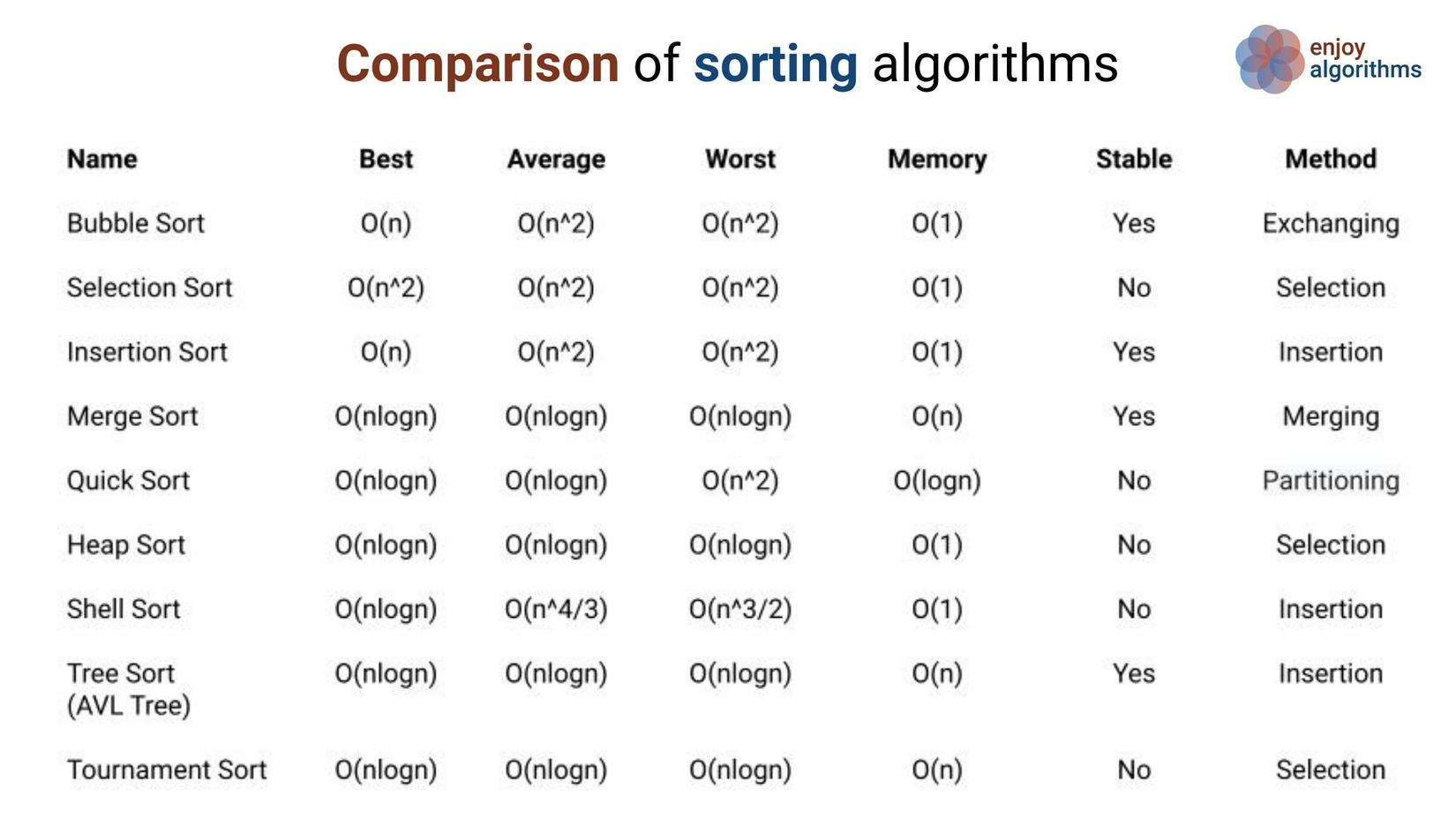
So sánh dựa trên độ hiệu quả

Các thuật toán sắp xếp dựa trên so sánh (based sorting)

Trong các thuật toán sắp xếp dựa trên so sánh, chúng ta so sánh các phần tử để xác định thứ tự của các phần tử trong mảng đầu ra cuối cùng đã sắp xếp. Tất cả các thuật toán sắp xếp dựa trên so sánh đều có cận dưới độ phức tạp là nlogn. Chúng ta đã thấy rằng bất kỳ thuật toán sắp xếp dựa trên so sánh nào cũng phải mất O(nlogn) thời gian để sắp xếp một mảng gồm n phần tử trong trường hợp xấu nhất.

• Bubble sort : so sánh các phần tử để đặt các phần tử lớn nhất vào vị trí cuối cùng.
• Selection sort: so sánh các phần tử để đặt các phần tử nhỏ nhất vào vị trí phía trước.
• Insertion sort: so sánh các phần tử để quyết định vị trí của một phần tử trong mảng đã được sắp xếp một phần.
• Merge sort: so sánh các phần tử của hai phần tử đã sắp xếp để hợp nhất chúng thành mảng được sắp xếp cuối cùng.
• Quicksort: so sánh các phần tử của phân vùng mảng chưa được sắp xếp thành hai nửa khác nhau xung quanh giá trị pivot.
• Heapsort: so sánh các phần tử trong quá trình heapify để đặt các phần tử nhỏ nhất lên phía trước của mảng (Nếu chúng ta đang sử dụng min-heap).

Như chúng ta đã thấy, độ phức tạp về thời gian trong trường hợp xấu nhất của các thuật toán sắp xếp ở trên có thể được phân loại thành hai phần:O(n^2) và O(nlogn).

Các thuật toán sắp xếp O(n^2): bubble sort, selection sort và insertion sort. Các thuật toán sắp xếp: O(nlogn): mergesort, quicksort, heapsort. Lưu ý: Hiệu suất trong trường hợp xấu nhất của quicksort là O(n^2), nhưng trung bình nó hoạt động rất nhanh ở độ phức tạp thời gian O(nlogn). Trên thực tế, khả năng xảy ra trường hợp xấu nhất là rất thấp khi tất cả các mảng đầu vào đều có khả năng xảy ra như nhau.

Ngoài các phép toán so sánh, chúng ta còn thực hiện các dạng phép toán khác trong các thuật toán sắp xếp này. Nhưng số lượng các phép toán này sẽ luôn ít hơn số lượng các phép toán so sánh. Đó là lý do tại sao thao tác so sánh là yếu tố quyết định độ phức tạp của thời gian.

• Bubble sort: hoán đổi
• Selection sort: hoán đổi
• Insertion sort: sàng lọc
• Merge sort: phân bổ thêm bộ nhớ và sao chép dữ liệu
• Quicksort: hoán đổi
• Heapsort: hoán đổi

Các thuật toán so sánh tuyến tính

Có những thuật toán sắp xếp chạy nhanh hơn độ phức tạp thời gian O(nlogn), nhưng chúng yêu cầu các giả định đặc biệt về thứ tự đầu vào để xác định thứ tự sắp xếp của các phần tử. Các thuật toán sắp xếp này sử dụng các phép toán khác với phép so sánh để xác định thứ tự đã sắp xếp và hoạt động với độ phức tạp thời gian O(n). Vì vậy, cận dưới O(nlogn) không áp dụng cho các thuật toán sắp xếp này.

Ví dụ về các thuật toán sắp xếp chạy trong thời gian tuyến tính là counting sort, radix sort, bucket sort,... Counting sort và radix sort giả định rằng đầu vào bao gồm các số nguyên trong một phạm vi nhỏ. Đồng thời, bucket sort giả định rằng đầu vào được tạo ra bởi một quá trình phân phối ngẫu nhiên các phần tử một cách đồng nhất trong khoảng nhất định.

Các điều kiện đặc biệt với thuật toán sắp xếp thời gian tuyến tính:

• Counting sort: mỗi phần tử đầu vào là một số nguyên trong phạm vi từ 0 đến k.
• Radix sort: Cho n số nguyên trong đó mỗi số nguyên có thể nhận tối đa k giá trị có thể.
• Bucket sort: Đầu vào được tạo ra bởi quá trình phân phối ngẫu nhiên các phần tử một cách đồng nhất và độc lập trong khoảng [0, 1).

Dưới đây là so sánh độ phức tạp về thời gian và không gian của một số thuật toán sắp xếp phổ biến:

Các thuật toán sắp xếp tại chỗ (in-place)

Thuật toán sắp xếp được áp dụng tại chỗ nếu nó không sử dụng thêm không gian để thao tác đầu vào nhưng có thể yêu cầu một không gian bổ sung nhỏ mặc dù không đủ cho hoạt động của nó. Hoặc chúng ta có thể nói một thuật toán sắp xếp sắp xếp tại chỗ nếu chỉ có một số lượng không đổi các phần tử mảng đầu vào được lưu trữ bên ngoài mảng.

• Các thuật toán sắp xếp tại chỗ: bubble sort, selection sort, insertion sort, quicksort, heapsort
• Các thuật toán sắp xếp với không gian bổ sung: merge sort, counting sort

Các thuật toán sắp xếp ổn định

Thuật toán sắp xếp ổn định nếu nó không thay đổi thứ tự của các phần tử có cùng giá trị

Các thuật toán sắp xếp ổn định: buble sort, insertion sort, merge sort.

Các thuật toán sắp xếp không ổn định: selection sort, quicksort, heapsort, counting sort.

Các thuật toán sắp xếp ổn định hoạt động theo quy tắc: nếu hai mục so sánh bằng nhau thì thứ tự tương đối của chúng sẽ được giữ nguyên, tức là nếu cái này đứng trước cái kia trong đầu vào thì nó sẽ đứng trước cái kia trong đầu ra.

Tính ổn định là điều cần thiết để duy trì thứ tự sắp xếp trên cùng một tập dữ liệu.

Tính ổn định cũng không phải là vấn đề nếu tất cả các khoá đều khác nhau.

Các thuật toán sắp xếp không ổn định có thể được triển khai đặc biệt để ổn định. Một cách để làm điều này là mở rộng thao tác so sánh để so sánh giữa hai đối tượng dữ liệu có khoá bằng nhau được quyết định bằng cách sử dụng thứ tự của các mục nhập trong dữ liệu đầu vào ban đầu như một bộ ngắt (tie-breaker).

Tuy nhiên, việc ghi nhớ thứ tự này có thể cần thêm thời gian và không gian.

Thuật toán sắp xếp trực tuyến và ngoại tuyến

Thuật toán chấp nhận một phần tử mới trong khi quá trình sắp xếp đang diễn ra được gọi là thuật toán sắp xếp trực tuyến. Một thuật toán trực tuyến có thể xử lý từng phần đầu vào của nó theo thứ tự nối tiếp. Nói cách khác, các thuật toán sắp xếp trực tuyến có thể sắp xếp dữ liệu mà không cần có toàn bộ dữ liệu đầu vào ngay từ đầu.

Ví dụ: insertion sort xem xét một phần tử đầu vào mỗi lần lặp và tạo ra giải pháp được sắp xếp một phần mà không xem xét các phần tử trong tương lai. Vì vậy, duy trì một danh sách được sắp xếp trong sắp xếp chèn, chúng ta có thể đặt từng mục đầu vào vào đúng vị trí của nó khi chúng ta nhận được thông tin đầu vào. Vì vậy, insertion sort là một thuật toán sắp xếp trực tuyến.

Ngược lại, thuật toán ngoại tuyến cần dữ liệu đầu vào đầy đủ trong bộ nhớ ngay từ đầu hoặc nó yêu cầu tất cả các mục phải ở trong bộ nhớ trước khi bắt đầu sắp xếp. Ví dụ: Thuật toán selection sort sắp xếp một mảng bằng cách liên tục tìm phần tử nhỏ nhất từ phần chưa được sắp xếp và đặt nó ở đầu. Nó luôn yêu cầu quyền truy cập vào toàn bộ đầu vào, vì vậy nó là một thuật toán ngoại tuyến.

So sánh dựa trên các phương pháp tiếp cận giải quyết vấn đề

• Cách tiếp cận chia để trị: merge sort và quicksort
• Cách tiếp cận gia tăng việc sử dụng các vòng lặp lồng nhau: bucket sort, selection sort, insertion sort.
• Giải quyết vấn đề bằng cách sử dụng cấu trúc dữ liệu: heapsort, tree sort
• Giải quyết vấn đề bằng cách sử dụng băm: counting sort.

Suy nghĩ thêm

• Hiểu các thuật toán sắp xếp là cách tốt nhất để học cách giải quyết vấn đề và phân tích độ phức tạp trong các thuật toán. Trong một số trường hợp, chúng ta thường sử dụng sắp xếp như một thói quen chính để giải quyết một số vấn đề về code
• Giống như insertion sort, quicksort có code chặt chẽ và yếu tố hằng số ẩn trong thời gian chạy của nó là nhỏ.
• Insertion sort có thể được ưu tiên khi mảng đầu vào gần như được sắp xếp hoặc kích thước đầu vào nhỏ.
• Insertion sort hiệu quả hơn so với thuật toán bubble sort và selection sort.
• Việc biết thuật toán nào là tốt nhất có thể phụ thuộc rất nhiều vào các chi tiết của ứng dụng và cách triển khai. Quicksort là một thuật toán phổ biến để sắp xếp các mảng đầu vào lớn trong hầu hết các tình huống thực tế vì thời gian chạy dự kiến của nó là O(nlogn). Nó cũng hoạt động tốt hơn heapsort trong thực tế.
• Merge sort là lựa chọn tốt nhất để sắp xếp một danh sách được liên kết. Tương đối dễ thực hiện merge sort trong trường hợp này chỉ cần thêm O (1) không gian. Mặt khác, hiệu suất truy cập ngẫu nhiên hạn chế của danh sách liên kết làm cho một số thuật toán khác, chẳng hạn như quicksort, hoạt động kém và những thuật toán khác như heapsort hoàn toàn không thể thực hiện được.
• Chúng ta có thể thực hiện song song sắp xếp trộn nhờ phương pháp chia để trị, trong đó mọi bài toán con nhỏ hơn đều độc lập với nhau.
• Nếu sự ổn định là cần thiết và không gian có sẵn, merge sort có thể là lựa chọn tốt nhất để triển khai.
• Làm thế nào chúng ta có thể cải thiện thời gian chạy của quicksort bằng cách tận dụng thời gian chạy nhanh của insertion sort khi đầu vào của nó gần như được sắp xếp?
• Làm cách nào chúng ta có thể sửa đổi thuật toán quicksort để làm cho nó ổn định?
• Làm cách nào chúng ta có thể triển khai quicksort và merge sort lặp đi lặp lại bằng cách sử dụng ngăn xếp?
• Một số thuật toán sắp xếp bổ sung để khám phá: Shell sort, Tree sort, and Tournament sort.

Nguồn

enjoy algorithms