Hồi quy tuyến tính là gì?

Hồi Quy (regression) là một phương pháp học có giám sát (supervised learning) trong Máy Học. Mục tiêu chính là tìm ra mối quan hệ giữa các đặc trưng của một vấn đề nào đó. Cụ thể hơn, từ một tập dữ liệu cho trước, ta xây dựng một mô hình (phương trình, đồ thị, …) khớp nhất với tập dữ liệu, thể hiện được xu hướng biến thiên và mối quan hệ giữa các đặc trưng. Khi có một mẫu dữ liệu mới vào, dựa vào mô hình, chúng ta có thể dự đoán giá trị của mẫu dữ liệu đó. Lấy ví dụ như chúng ta cần dự đoán xác suất thoát FA của một thanh niên dựa vào số lượng tin nhắn cho Crush và tốc độ trung bình mà Crush rep tin nhắn lại. Như vậy chúng ta cần tìm mối quan hệ của khả năng thoát FA phụ thuộc vào số lượng tin nhắn và tốc độ rep tin nhắn của Crush. Ta xây dựng phương trình 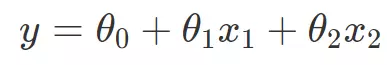Trong đó y là khả năng thoát FA phụ thuộc x1 (số lượng tin nhắn cho Crush) và x2(tốc độ rep tin nhắn của Crush). Sau khi có được các giá trị θ thì ta có được phương trình cụ thể. Khi đó khi có thêm một mẫu dữ liệu của một thanh niên mới, chỉ cần áp dụng vào phương trình chúng ta sẽ biết được khả năng thanh niên đó có thoát FA hay không.

Trong ví dụ trên, ta thấy phương trình 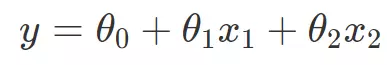là phương trình của mặt phẳng trong không gian 3 chiều. Những mô hình tương tự như phương trình đường thẳng, phương trình mặt phẳng chính là những mô hình tuyến tính. Hồi quy tuyến tính (linear regression) là một mô hình đơn giản trong bài toán hồi quy, trong đó chúng ta dùng đường thẳng, mặt phẳng, hay phương trình tuyến tính nói chung để dự đoán xu hướng của dữ liệu. Giải bài toán hồi quy tuyến tính chính là đi tìm các tham số θ0, θ1, ... để xác định phương trình tuyến tính 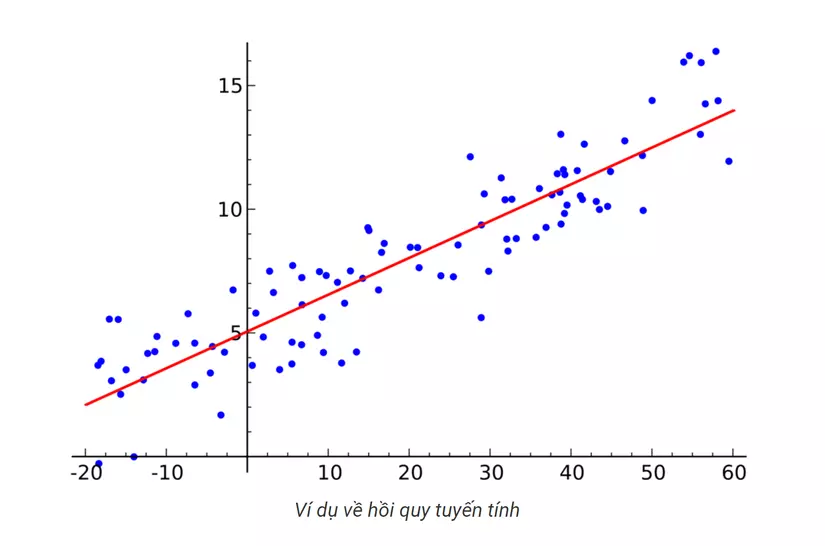Mô hình hồi quy tuyến tính thường được trang bị bằng cách tiếp cận bình phương nhỏ nhất, nhưng cũng có thể tiếp cận bằng những cách khác như giảm thiểu sự "thiếu phù hợp" (độ lệch tuyệt đối nhỏ nhât trong hồi quy) hoặc bằng cách giảm thiểu penalty của bình phương nhỏ nhất (loss function trong hồi quy norm L2)

Xác định công thức

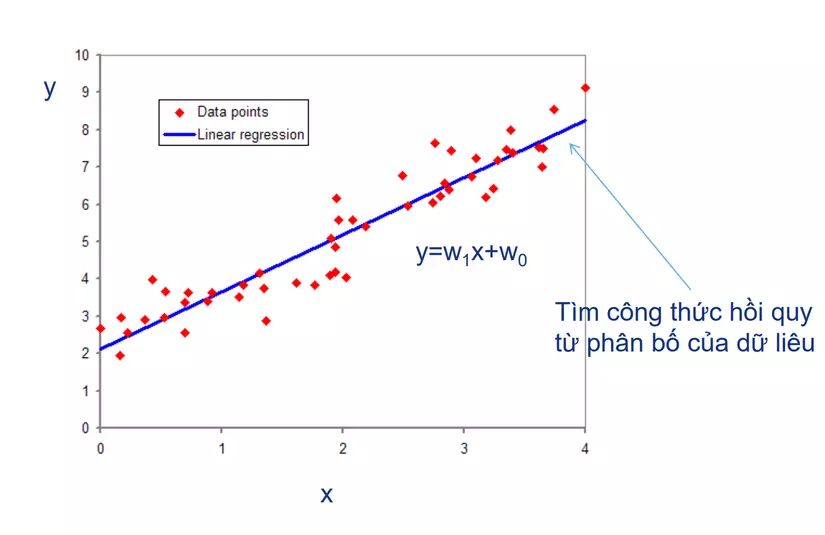
• Vector input: X
• Output là một hàm tuyến tính theo X
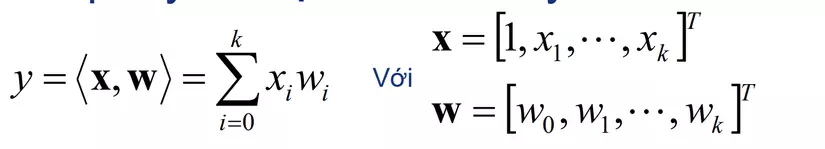
• Tổng quát hóa khi dữ liệu chứa nhiễu
• Khi có N cặp dữ liệu huấn luyện (y, X) ta cần phải tìm w sao cho sai số bình phương nhỏ nhất.
• w được tính toán bởi
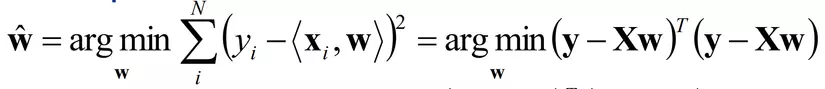
• Giải hệ phương trình
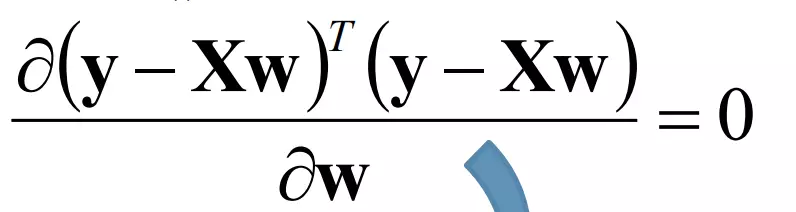
• Công thức

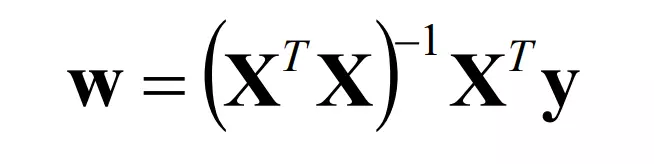
Tổng quát hóa mô hình tuyến tính

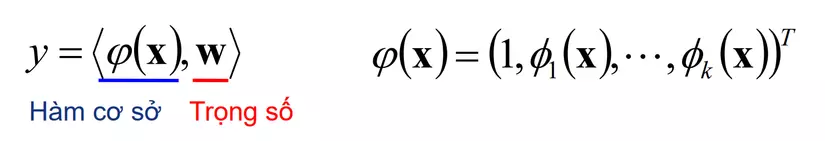
• Khi có N cặp dữ liệu huấn luyện (y, X) ta cần phải tìm w sao cho sai số bình phương nhỏ nhất.
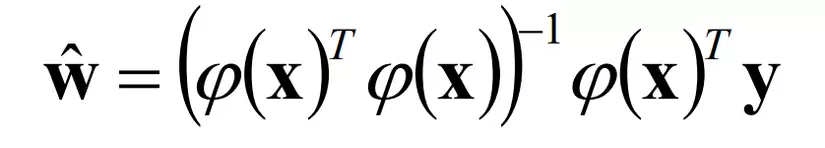
• Một số hàm cơ sở dùng trong công thức

1. Polynominal
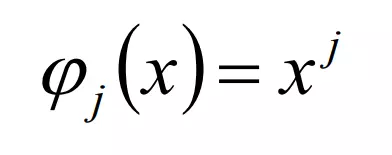
2. Gaussian
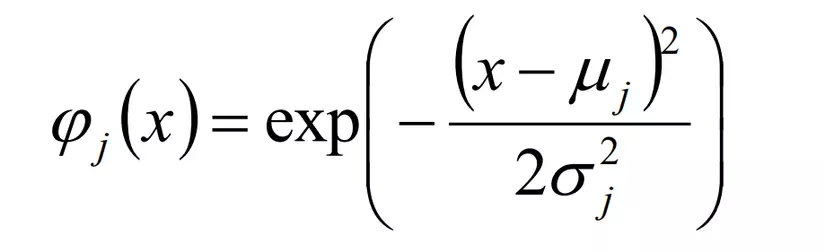
3. Sigmoidal
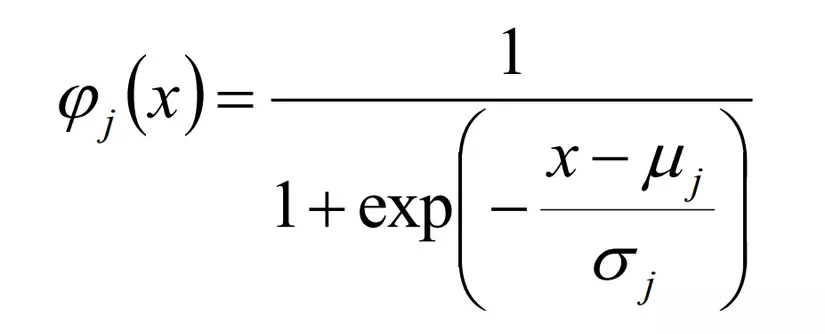
4. Fast Fourier

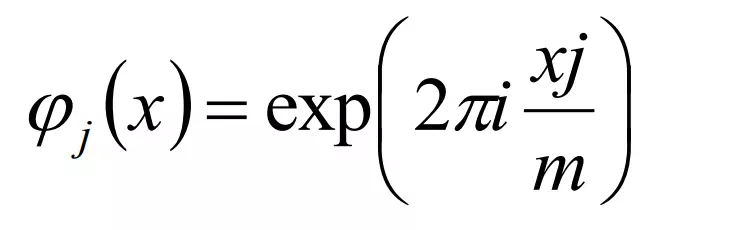
• Công thức tổng quát
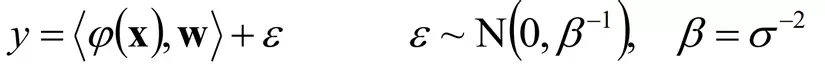
• <X,y> là dữ liệu huấn luyện
• W, Beta là các tham số cần tìm để có bình phương nhỏ nhất
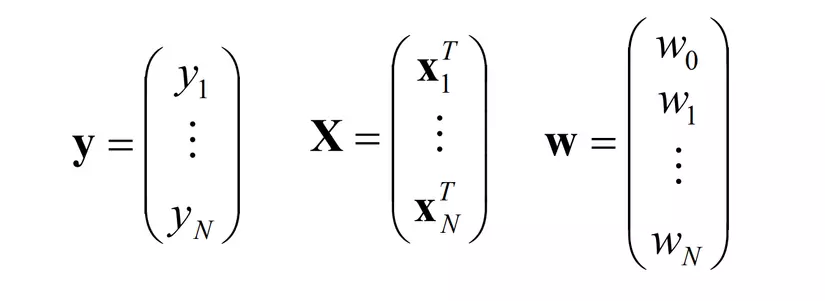
• Công thức tính độ chính xác Beta ( chính là sai số bình phương trung bình giữa giá trị dự đoán và giá trị thực tế)

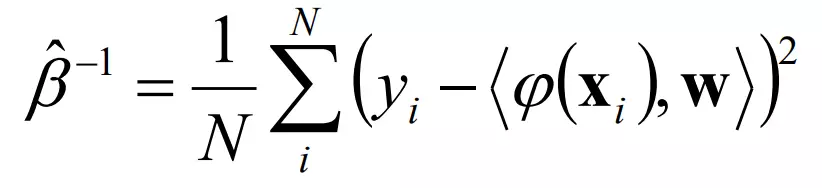
Nhược điểm và một số phương pháp hỗ trợ

• Khi dữ liệu lớn công thức hiện tại có độ phức tạp lớn 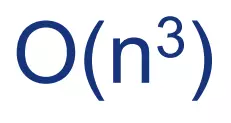để tính ma trận nghịch đảo
• Phương pháp Gradient Descent (phương pháp rơi dốc)
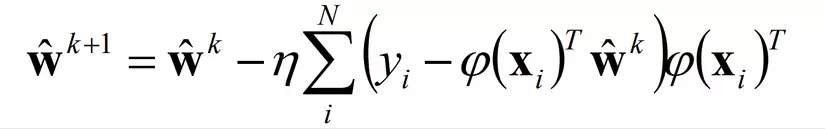
• Dạng hợp thức hóa (chi tiết bên dưới)

Hợp thức hóa (tại sao lại áp dụng)

• Mô hình học càng “phức tạp” thì càng dễ xấp xỉ với dữ liệu huấn luyện. Tuy nhiên lại khó với dữ liệu tương lai. Đây là vấn đề học quá (over fitting) trong học máy.
• Để tránh hiện tượng này ta “hợp thức hóa” mô hình bằng “Hàm tổn thất”(loss function).
• Việc hợp thức hóa mô hình cũng được sử dụng trong việc cắt giảm số chiều dữ liệu.
• Hạng hợp thức tổng quát
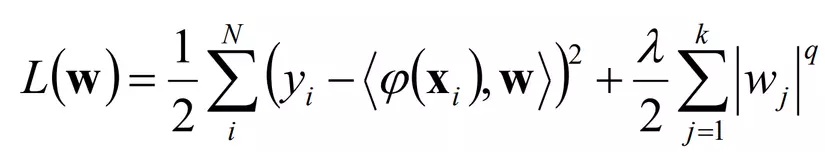
• q=2: Hợp thức hóa L2
• q=1: Hợp thức hóa L1 hay Least Absolute Shrinkage and Selection Operator-LASSO