Sharpen your Coding Skills - Elevator Puzzle

Introducing Melvin and Bugsy, characters who are the creation of Joe Celko who has joined the team to give you an opportunity to sharpen your coding skills with puzzles that will both amuse and torment you. Joe Celko is best known as the database expert who writes books on SQL, data and databases. But before that, he was an honest developer obsessed with finding good algorithms and clean code. Put on your thinking cap as we assist Melvin Frammis and the rest of the programming staff at International Storm Door and Software write beautiful code in whatever programming language they have.

• The Elevator Problem

“Bugsy, what are you doing?” asked Melvin Frammis as he came to the lobby of the company office. Bugsy Cottman is a junior programmer at International Storm Door & Software, where they both work., Bugsy often makes up for his lack of skill with blind enthusiasm and today he was disassembling the control panel of one of the elevators. “I am going to automate the elevators, and speed up travail time. It can save us millions in lost employee time!” replied Bugsy. “Was there a problem?” “Of course!”, said a mildly vexed Bugsy.“Did you notice that when you want to go up, the elevator is going down, and vice verse?” Melvin shook his head. The odds of getting an elevator going in one particular direction depends on the floor and its not 50-50 as you might think. Imagine a two story building; the lobby elevator is going up 100% of time and the top floor elevator is going down 100% of the time. “I got a speech gizmo and a badge scanner so that when someone steps into the car, we can read their floor from the badge and tell them to get on or off at a floor until they get to where they want to be.” said Bugsy. “That is not much of an improvement over a button and the built in scale to count the number of people we have now” Said Melvin, looking for the stairwell door. “But I am writing a program that will optimize overall travel time by telling people to get on and off the car, even if they are not at their destination floor. Here is the spec: The building has (n) floors numbered from one to (n) The car holds (p) passengers. Exactly (p) passengers want to get to each floor. The passengers start off randomly distributed over the floors and there are (p) of them on each floor. The goal is to minimize the total distance the car travels measured in floors. “This is a sorting problem with some weird restrictions” said Melvin. “I might get to a floor, get out and then get back on when the car comes to me again. I am not sure if people will like that.” “Hey, I want to save elevator time, not worry about those silly-ass 'people skills' my stupid boss says I don't have!” “Bugsy, when you put out the fire, come on up and I will write a short program you. You are not old enough to recognize it, but this is what is known as a bi-directional one-tape sort. We will just use one dimensional arrays, say, ten floors and five passengers per floor and in the car. ” Bugsy said, “What is a tape drive? And what fire?” as he looked up and saw the answer to his second question in the form of smoke coming from the wall of the elevator. There is nothing more dangerous than a programmer with a screwdriver,

• ANSWER

Knuth, Donald, The Art Of Computer Programming. Vol 3, pp 357-360.”One tape sorting”. You can also look up Karp's algorithm. The key to the algorithm is not to treat the people already in the elevator as any different to the people waiting for the lift. The algorithm works with an up and a down mode of operation. You also need to keep track of the number of people wanting to move higher than a given floor and those wanting to move lower. This is a complicated piece of book-keeping but it is what makes the algorithm work, so we can't avoid it. On each floor k you need to count uk the number of people on that floor and below it who want to go higher than that floor. So if there is one person on each floor wanting to go to the floors as indicated, then uk for floor 3 is 1 because on floor 3 and below there is only one person wanting to go higher than floor 3. For floor 2 uk is 2 because there are two people wanting to go higher than floor 2 who are on floor 2 or below.

You can see the other values for uk in the table.

Up The basic idea is to start in the lobby and fill the car with passengers with the highest possible destination floor - as the car is finite some might not get on. Move up one floor i.e. k=k+1. Drop off all the passengers off the next floor up to create a combined pool of passengers waiting for the elevator. (They don't all have to get out as long as the passengers to the next floor are picked from the combined group so as to be traveling to the highest floors.) Adjust the values of uk based the total passengers on the floor and in the lift. As long as uk>0 keep going up. Allow passengers with the highest possible destination floor to get onto the elevator and move to floor k+1 Yes some passengers have had to get out a the wrong floor - but as Knuth says "This represents their sacrifice for the common good".

Down If there are no passengers on the floor or below wanting to go higher then we switch to the down-moving mode. Treating all of the passengers on the floor and in the lift as a single pool, let on the passengers who want to go to the lowest floors. Move down to floor k-1 and adjust or recompute the values of uk based the total passengers on the floor and in the lift. As long as uk-1>0 keep going down - notice that is the floor below's value that is tested. If uk-1=0 and uk=0 keep going down - otherwise switch to going up. Repeat until everyone is where they want to be. You should be able to see that this algorithm corresponds to picking at each floor the passengers who want to travel the maximum distance in the current direction - irrespective of whether they are already on the lift or not. The really clever bit is working out when to change direction of travel based on the total number of people who want to move up at or below the floor. This is is Karp's algorithm and it is proved to be the way to get everyone to the right floor in the minimum total time.

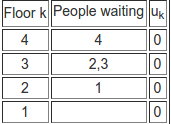
The simplest case to illustrate the algorithm is if there is one person per floor and the elevator car only holds one person. Suppose we start with:

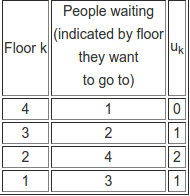
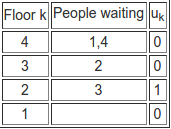
Where the numbers in the people waiting column shows which floor the people want to be on. The first up phase takes the person wanting to go to floor 3 and moves up to floor 2 - where they all get out to produce:

Notice that we have updated uk to take account of the new arrangement of people. As u2 is non-zero we keep moving up. Now the passenger that wants to go to the highest floor is floor 4. This means the passenger who got on at floor 1 is left behind on the wrong floor. This gives:

As u3 is non-zero we keep moving up. In this case the passenger riding to the fourth floor stays in the lift and makes it to their floor at the next step.

As u4 is zero we switch to moving down. We now select passengers wanting to go to the lowest floors hence the passenger wanting to go to floor 1 gets in.

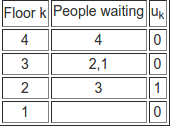
Notice that at this point we don't switch back to going up because uk-1=u2 is non-zero. Thus, the person wanting to move to floor 1 moves to floor 2.

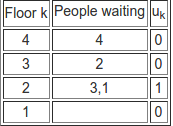
At this point uk-1=u1 is zero so we switch to the going up mode and the person wanting to go to floor 3 gets in the lift which takes them to floor 3.

At this point uk-1=u2 is zero so we switch to the going down mode and the person wanting to go to floor 2 gets in the lift which takes them to floor 2.

A this point we have uk-1=u1=0 and you might think that we need to switch direction, but as uk=0 we continue moving down. You can see that this extra condition is needed to complete the move. One last move down delivers the final person to the correct floor.

And with this the job is done. Of course to see the algorithm really work you need to have more floors, more people and a bigger car. But the idea of getting everyone out at each floor and then picking the ones going the maximum distance in either the up or down direction is the key to the algorithm.