Giới thiệu về mã Hoá RSA

1. Nguyên Nhân Hình Thành

An toàn bảo mật

Đối mặt với các vụ tấn công, lấy định danh người dung.

Các yếu tố xác thực ngày càng nhiều.

=> Công nghệ bảo mật xác thực mạnh chính là dựa trên cơ sở mã hóa thông tin.

Mã hoá:

Mã hoá cổ điển.

Mã hoá đối xứng.

Mã hoá bất đối xứng: là hệ mã hóa sử dụng khóa để mã hóa và khóa để giải mã khác nhau. Trên cơ sở phân tích số nguyên thành thừa số nguyên tố, sau này thành hệ mã hóa RSA nổi tiếng và được ứng dụng rộng rãi hiện nay.

2. RSA Và Chữ ký số

Chữ ký số là một dạng của chữ ký điện tử. Nó là một dạng dữ liệu dùng để chứng thực cho các dữ liệu khác

Chữ ký số sử dụng một hệ mã hóa bất đối xứng. Trong phần lớn các trường hợp, nó còn có thể kiểm tra cả tính toàn vẹn của dữ liệu nữa.

Chữ ký số tương tự như chữ ký tay trên nhiều phương diện, nhưng việc cài đặt và sử dụng chữ ký số khó khăn hơn rất nhiều.

Cách sử dụng chữ ký số

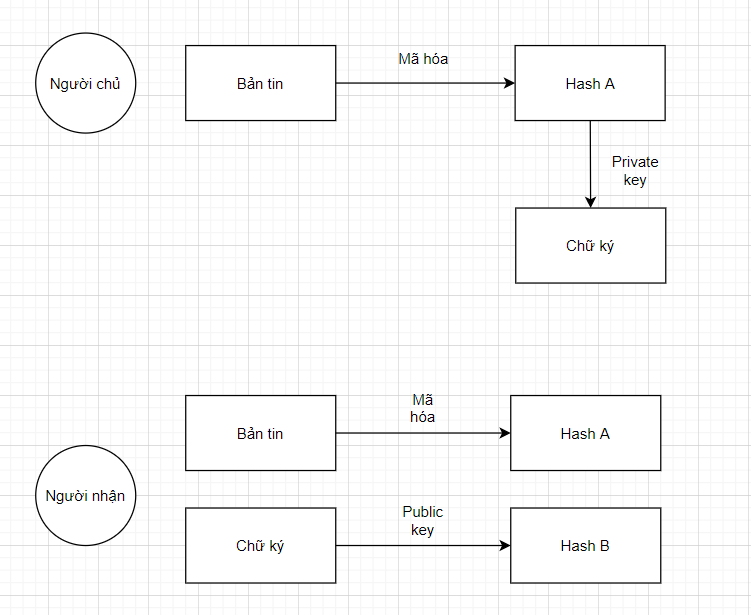
Việc ký tên và xác thực chữ ký số sử dụng hệ mã hóa RSA tương tự như quá trình mã hóa mà giải mã ở trên. Tuy nhiên vai trò của public key và private thì có thay đổi đôi chút.

Nên sử dụng hash cho chữ ký số

1 bản tin có thể sẽ rất dài nên việc sử dụng hash của bản tin sẽ làm giảm đi thời gian cũng như kích thước của ký tự

Các hàm hash là hàm 1 chiều, vì vậy dù có được hash cũng không thể biết được bản tin gốc như thế nào.

Độ dài hash là cố định và thường rất nhỏ, vì vậy chữ số sẽ không chiếm quá nhiều dung lượng

Giá trị hash còn có thể dùng để kiểm tra lại bản tin nhận được có nguyên vẹn hay không?

Cách chữ ký số hoạt động

Lợi ích

Giả mạo chữ ký hay giả mạo văn bản: văn bản chỉ có thể được ký nếu có khóa bí mật (được giữ bí mật bởi người ký). Do đó kẻ mạo danh không thể ký thay giùm người ký.

Chỉnh sửa văn bản đã ký: chỉnh sửa văn bản đã ký sẽ tạo ra một giá trị băm khác giá trị băm gốc được dùng để ký văn bản. Do vậy, người xác thực chữ ký sẽ có thể phát hiện văn bản đã bị chỉnh sửa nhờ so sánh 2 giá trị băm với nhau.

Không thoái thác được chữ ký của mình: nếu mọi người đều biết khóa công khai đó thuộc về người ký thì chữ ký trên văn bản đó phải thuộc về người ký. Người ký không thể phủ nhận được việc đã ký văn bản đó.

Một số điều cần áp dụng

Khi sử dụng với chữ ký số, hàm băm này phải đảm bảo về mặt bảo mật, ví dụ như SHA-256, tức gần như là không thể để tìm ra 2 văn bản nào có cùng 1 giá trị băm.

Gắn kèm chữ ký số vừa tạo với văn bản được ký.

Sử dụng tạo chữ ký điện tử khi sử dụng những ứng dụng thường dùng như Word, Excel

3. Cách Tạo Khoá

Theo định lý Fec-ma: với p là số nguyên tố, với mọi m < p: mp-1 = 1 (mod p)

Với q là một số nguyên tố khác p, và m nguyên tố cùng nhau với cả p và q, ta có: [mp-1]q-1 = 1 (mod p)

tương tự với q: [mq-1]p-1 = 1 (mod q) => m(q-1)(p-1) = 1 (mod pq)

Lũy thừa 2 vế lên s lần (s nguyên dương) và nhân 2 vế cho m: ms(q-1)(p-1)+1 = m(mod pq)

Công thức cơ bản của mã hóa RSA ms(q-1)(p-1)+1 = m(mod pq)

Phân tích s(q-1)(p-1)+1 thành tích của 2 khóa: chọn e nguyên tố cùng nhau với (q-1)(p-1)

=> tồn tại nghịch đảo d của e sao cho: ed=1 (mod (p-1)(q-1)) hay: ed=s(p-1)(q-1) +1

Tóm lại: med = m(mod pq)

Mấu chốt cơ bản của việc sinh khóa trong RSA là tìm được bộ 3 số tự nhiên e, d và n sao cho: cần bảo mật cho d sao cho dù biết e, n hay thậm chí cả m cũng không thể tìm ra d được.

=> Cụ thể, khóa của RSA được sinh như sau:

Chọn 2 số nguyên tố p và q

Tính n = pq. Sau này, n sẽ được dùng làm module trong cả public key và private key.

Tính một số giả nguyên tố bằng hàm Carmichale như sau: λ(n) = BCNN(λ(p), λ(q)) = BCNN(p − 1, q − 1)

Giá trị này sẽ được giữ bí mật.

Chọn một số tự nhiên e trong khoảng (1, λ(n)) sao cho e và λ(n) nguyên tố cùng nhau ƯCLN(e, λ(n)) = 1

Tính toán số d là nghịch đảo modulo của e theo modulo mod λ(n) d ≡ 1/e (mod λ(n)) hay de ≡ 1 (mod λ(n)).

Public key sẽ là bộ số (n, e), và private key sẽ là bộ số (n, d).

=> Giữ private key thật cẩn thận cũng như các số nguyên tốp và q vì từ đó có thể tính toán các khóa rất dễ dàng.

4. Mã Hoá và Giải Mã

Sau khi đã nhận được public key(e,n) và private key (d) :

Ecryption: me mod n = c

Decryption: cd mod n = m

Trong đó:

m là message ban đầu.

e, n là public key.

c là dữ liệu đã được mã hóa.

d là private key thường là số rất lớn, tích của hai số nguyên tố.

Ví dụ: ta có public key( e =7, n = 33) và private key( d= 3 ) và giả sử cho m = 2 Encryption is c = 27 mod 33 = 29

Descryption is m = 293 mod 33 = 2

c là bản mã.

d là bản rõ.

Tổng kết lại ta có các thông số sau:

p=3

q=11

φ(n) = 20

n =33

e=7

d = 3

Tổng kết về thuật toán RSA:

Là 1 thuật toán mã hóa bất đối xứng.

Cơ chế của thuật toán dựa trên 4 bước chính:

Sinh khóa

Chia sẻ key

Mã hóa

Giải mã

Tính an toàn của RSA chủ yếu dựa vào bố tạo số ngẫu nhiên sinh ra 2 số nguyên tố p và q ban đầu.

Việc tính ngược lại p và q từ n là chuyện hầu như không thể với hai số nguyên tố 2048 bít .

Nhưng việc tính ra d từ p và q là việc rất dễ dàng.

Do vậy, nếu như một bên nào đó đoán ra được hoặc tìm ra lỗ hổng của bộ sinh số ngẫu nhiên đó thì coi RSA bị hóa giải.

Gần đây có ý kiến cho rằng Bộ An ninh Nội địa Hoa Kỳ (NSA) đã cài một backdoor vào bộ tạo số ngẫu nhiên Dual Elliptic Curve để giúp NSA có thể crack RSA nhanh hơn 10,000 lần.

5. Điểm Yếu và Cách Tấn Công

Số n nhỏ

Nếu số n nhỏ ( chiều dài n < 256 bit), số n có thể bị tách ra thành các thừa số nguyên tố dễ dàng bởi các công cụ có sẵn như factordb.

Chiều dài của số n được khuyến cáo là 1024 bit.

Nhưng đã có những trường hợp số n lớn, nhưng phân tách của n thành thừa số nguyên tố đã có sẵn trong cơ sở dữ liệu của các trang như factordb hoặc alpertron.

Đây là 1 cách tìm p và q rất dễ nên thường được thử đầu tiên.

Số e nhỏ, số m nhỏ

1 nhược điểm lớn của mã hoá RSA đó là tốc độ mã hoá chậm hơn nhiều so với mã hoá DES, do vậy trong một vài trường hợp để tăng tốc độ, người mã hoá sẽ mã hoá tài liệu bằng 1 mã hoá khác nhưng khoá sẽ được mã hoá bằng RSA.

Đồng thời để tối ưu hoá thời gian mã hoá, số e cũng được chọn theo dạng e = 2n+1, khi đó e nhỏ nhất là e = 3.

Nếu ta chọn số e nhỏ và tin nhắn M (m nhỏ) -> ciphertext: c = m3 (mod n). Vì m nhỏ nên m3 < n khi đó phép toàn module không có tác dụng, Vì vậy để tìm người lại m từ c ta cso m = c1/3

Tấn công lặp liên tục

Ban đầu ta có 2 số p, q lần lượt là 3, 5 => n = p*q = 15 => chọn m = 7.

Tính φ(n) = (p-1)*(q-1) = 8 => chọn e = 3.

Tính c = me mod n = 13

c1 = ce mod n = 7

c2 = c1e mod n = 13

Do c2 = c => m = c1 = 7

Hiệu p – q nhỏ - Fermat Attack

p, q được chọn có cùng độ dài bit để tạo được 1 mã RSA mạnh, nhưng điều này có thể khiến q,p quá gần nhau khiến cho kẻ tấn công dễ dàng phân tách n thành thừa số nguyên tố. Điều kiện ( p – q ) < n¼

Số e trùng nhau, số e nhỏ - Hastad Broadcast Attack

Trong mạng LAN, đôi khi số e được đặt giống nhau đối với các máy tình cùng mức độ. Nghĩa là e1 = e2 = ... = e = 3

Kịch bản tấn công xảy ra nếu máy chủ gửi cùng 1 tin nhắn broadcast m (đã được mã hóa thành c1, c2, ... cho nhiều máy tính trong mạng, và ta bắt được ít nhất e ciphertext c1, c2, ..., ce. Lúc này, ta sẽ có thể khôi phục lại plaintext m không mấy khó khăn.

Giả sử e = 3, đặt M = m3. Nhiệm vụ của ta là giải hệ phương trình đồng dư:

Sau khi tính được M, ta sẽ tìm được m ( bằng căn bậc 3 của M)

Số n trung nhau - Common modulus

Giống với ví dụ ở phần trước nhưng thay vì e trùng nhau, lần này n trùng nhau, nghĩa là n1 = n2 = ... = n và số e được chọn ngẫu nhiên. Như vậy mỗi thành viên trong mạng lưới sẽ được cấp một bộ tham số (n,ei,di ) riêng.

Vì ed ≡ 1 (mod φ(n)) nên tồn tại số k sao cho ed - kφ(n) = 1. Do đó: k = (ed-1)/φ(n) > (ed-1)/n

Vậy ta sẽ brute-force số k từ (ed-1)/n trở lên, tính ngược lại φ(n) = (ed-1)/k, cho đến khi thu được kết quả φ(n) là số nguyên. Có φ(n)ta dễ dàng tính được Private Key của victim: dvictim = evictim-1 mod φ(n)

Phân phối khoá

Giả sử C có thể gửi cho A một khóa bất kỳ và có thể khiến cho A tin đó là khóa công khai của B. Đồng thời C có thể đọc thông tin trao đổi giữa A và B. Khi đó, C sẽ gửi cho A khóa công khai của chính mình ( mà A nghĩ rằng đó là khóa của B ). Sau đó C sẽ đọc tất cả văn bản mã hóa do A gửi, giải mã với khóa bí mật của mình, giữ 1 bản copy, đồng thời mã hóa bằng khóa công khai của B và gửi cho B