Tại sao lại là Relation Database

Tôi chủ yếu làm việc với ngôn ngữ Android, để thử sức với Ruby on Rails tôi tìm hiểu về đặc khác biệt của Ruby on Rails so với Java. Có khá nhiều thứ, mức độ sâu rộng của database là một điểm căn bản lớn trong đó. Do vậy tôi đọc về database trong Rails và tìm thấy một chủ đề khá thú vị là Relation Database.

Chúng ta có rất nhiều cơ sở dữ liệu khác nhau: từ nhỏ và hữu ích như SQLite đến loại lớn mạnh như Teradata. Nhưng chúng ta có rất ít bài viết giải thích "database làm việc như thế nào?". Bạn có thể search google "how does a relational database work" và xem kết quả ít như thế nào. Hơn nữa, những bài viết đó đều rất ngắn. Bây giờ bạn hãy nhìn vào các công nghệ mới nhất hiện nay (như là Big Data, NoSQL hoặc JavaScript), bạn có thể tìm thấy rất nhiều bài viết giải thích các mà họ đã làm việc như thế nào.

Cơ sở dữ liệu rất là thú vị, bởi vì nó dựa trên các khái niệm hữu ích (useful) và tái sử dụng (reusable). Trước tiên bạn phải có một chút hiểu biết về database, làm sao để viết một số lệnh query nối bảng đơn giản, hoặc CRUD query đơn giản, nếu không có thể bạn sẽ không hiểu được bài viết này.

Bài viết sẽ bắt đầu với một số các khái niệm liên quan đến khoa học máy tính, như độ phức tạp, ... Có thể bạn sẽ không thích chủ đề đó, nhưng mà không có nó, bạn sẽ không hiểu được sự thông minh bên trong một cơ sở dữ liệu. Vì nó là một chủ đề lớn, nên ở đây bài viết chỉ tập chung vào những gì tôi nghĩ nó là quan trọng, cần thiết: Cách một cơ sở dữ liệu xử lý truy vấn SQL.

Độ phức tạp thuật toán

Đầu tiên hãy quay về vấn đề cơ bản(một số các khái niệm về độ phức tạp của thuật toán).

Từ thời xa xưa khi con người bắt đầu biết lập trình, các developers đã biết chính xác số lượng operations mà họ coding. Vì họ không muốn lãng phí tài nguyên CPU và memory, lúc đó máy tính rất chậm, và có cấu hình rất thấp. Trong phần này sẽ giới nhắc lại một số khái niệm và cần thiết để hiểu một database. Nó cũng sẽ giới thiệu một số khái niệm về "database index".

O(1) vs O(n^2) Ngày nay, rất nhiều developers không quan tâm đến độ phức tạp về thời gian truy vấn... và họ đúng.

Nhưng khi bạn đối mặt với một lượng dữ liệu lớn(không phải hàng ngàn mà là hàng triệu bản ghi) hoặc là bạn đang đối mặt với việc query trong thời gian rất ngắn được tính bằng mili giây thì việc hiểu khái niệm này trở nên rất quan trọng. Hoặc đôi khi databases của bạn phải đối mặt với cả hai vấn đề trên. Dưới đây sẽ đi cụ thể về khái niệm này:

Độ phức tạp (The time complexity) được sử dụng để xem trong thời gian bao lâu một thuật toán trả về một lượng dữ liệu. Để mô tả độ phức tạp, khoa học máy tính sử dụng kí hiệu toán học O. Kí hiệu này được được sử dụng với một hàm(function) bên trong nó mô tả có bao nhiêu operations trong một tuần toán cần để lấy được một lượng data nhất định.

Ví dụ: Khi nói thuật toán này là O(function_nào_đó()), nó có nghĩa là để lấy được lượng data cần thiết thì thuật toán đang dùng cần phải thực thi function_nào_đó() operations.

Khi mà lượng dữ liệu tăng lên thì số lượng operations cũng tăng lên một cách nhanh chóng. Bạn có thể xem biểu đồ dưới để thấy được sự thay đổi đáng kể khi lượng data tăng lên.

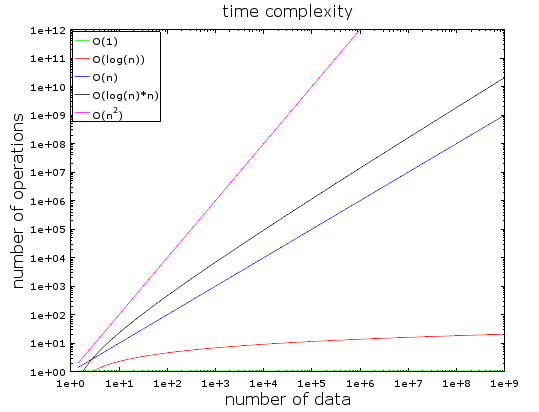
Với lượng data nhỏ, sự khác nhau giữa O(1) và O(n^2) là không đáng kể. Ta xét ví dụ sau với một thuật toán cần xử lý với 2000 phần tử(elements)

Với thuật toán có độ phức tạp O(1) sẽ tốn của bạn 1 operation Thuật toán có độ phức tạp O(log(n)) sẽ tốn của bạn 7 operations Thuật toán có độ phức tạp O(n) sẽ tốn của bạn 2000 operations Thuật toán có độ phức tạp O(n*log(n)) sẽ tốn của bạn 14 000 operations Thuật toán có độ phức tạp O(n^2) sẽ tốn của bạn 4 000 000 operations Nhìn vào đó có thể thấy được sự khác nhau giữa O(1) và O(n^2) vào khoảng 4 triệu operations nhưng mà bạn chỉ mất khoảng 2ms, nó là thời gian không đáng kể chỉ như một cái chớp mắt của bạn. Hiện nay, bộ vi xử lý có thể xử lý hàng trăm triệu phép tính mỗi giây. Đó chính là lý do vì sao hiệu suất và tối ưu hóa không phải là một vấn đề trong nhiều dự án công nghệ thông tin. Như đã nói ở trên thì khi lượng data tăng lên thì vấn đề này vẫn rất quan trọng để biết. Chúng ta sẽ thử nghiệm với lượng data lớn hơn khoảng 1 000 000 phần tử(elements)(đây cũng chưa phải là một big data).

Với thuật toán có độ phức tạp O(1) sẽ tốn của bạn 1 operation Thuật toán có độ phức tạp O(log(n)) sẽ tốn của bạn 14 operations Thuật toán có độ phức tạp O(n) sẽ tốn của bạn 1 000 000 operations Thuật toán có độ phức tạp O(n*log(n)) sẽ tốn của bạn 14 000 000 operations Thuật toán có độ phức tạp O(n^2) sẽ tốn của bạn 1 000 000 000 000 operations Không cần phải thực hiện các phép tính toán học bạn cũng có thể thấy rằng thuật toán với với độ phức tạp O(n^2) bạn có đủ thời gian để uống một ly cafe hoặc thậm chí là 2 tách. Nếu bạn thêm một số 0 vào lượng data xử lý thì bạn có thể có một giấc ngủ .

Một số lưu ý về độ phức tạp của thuật toán trong một số trường hợp như sau:

• Search trong một bảng băm tốt cho kết quả một phần tử có độ phức tạp O(1)
• Search trong một cây cân bằng tốt (well-balanced tree) cho kết quả một phần tử có độ phức tạp O(log(n))
• Tìm kiếm một phần tử trong mảng có độ phức tạp O(n)
• Thuật toán sắp xếp tốt nhất sẽ có độ phức tạp là O(n*log(n))
• Thuật toán sắp xếp tồi tệ nhất sẽ có độ phức tạp là O(n^2).

Dĩ nhiên chúng ta có những độ phức tạp còn tồi tệ hơn n^2 như:

• n^4: Một số thuật toán sẽ có độ phức tạp này(sẽ đề cập ở dưới)
• 3^n: Độ phức tạp trong một số thuật toán sử dụng trong rất nhiều databases
• factorial n: Với độ phức tạp này bạn sẽ không bao giờ thấy được kết quả kể cả với một lượng nhỏ data
• n^n: Nếu bạn kết thúc thuật toán với độ phức tạp này, bạn nên hỏi bản thân bạn có thực sự phù hợp với IT )

Dưới đây sẽ tìm hiểu một số thuật toán sort(trong databases)

Merge Sort

Bạn thường làm gì khi cần sort một collection? Bạn gọi phương thức sort(). Đó là một câu trả lời tốt, nhưng với một database bạn phải hiểu cách sort() function hoạt động như thế nào.

Chúng ra có rất nhiều thuật toán sorting tốt, nhưng ở đây bài viết sẽ tập chung vào thuật toán quan trọng nhất: the merge sort. Có thể bây giờ bạn không hiểu tại sao sorting data lại rất hữu ích, nhưng bạn sẽ hiểu ngay khi tìm hiểu đến phần tối ưu hóa truy vấn(query optimization). Hơn nữa am hiểu về the merge sort sẽ giúp bạn hiểu được join operation trong database hay còn gọi là the merge join.

Merge

Giống như rất nhiều thuật toán hữu ích khác, the merge sort phát triển dựa trên việc sáp nhập 2 mảng đã được sắp xếp có kích thước N/2 vào một mảng N phẩn tử được sắp xếp và nó chỉ mất N operations. The operation này được gọi là merge. Sẽ dễ hình dung hơn nếu bạn xem ví dụ dưới đây:

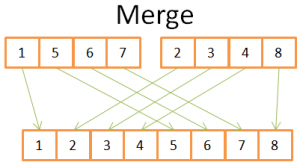
Bạn có thể nhìn thấy rằng để có được một mảng 8 phần tử đã được sắp xếp bạn chỉ cần một lần lặp của 2 mảng, mỗi mảng có 4 phần tử đã được sắp xếp: các bước merge như sau:

So sánh 2 phần tử đầu của 2 mảng lấy phần tử nhỏ hơn đẩy vào vị trí đầu tiên trong mảng 8 phần tử xét đến phần tử tiếp theo trong mảng có phần tử được đẩy vào mangt 8 phần tử, tiếp tục so sánh với phần tử của ảng bên kia, quay về bước 2, cứ tiếp tục lặp lại bước 1 và 2 cho đến khi một trong 2 mảng đã hết phần tử thì đẩy các phần tử còn lại của mảng còn lại vào mảng 8 phần tử ta được mảng 8 phần tử đã sắp xếp. Bạn có thể xem source code the merge sort như sau:

def merge_sort a
          return a if a.length == 1
          left,right = a.each_slice((a.size/2.0).round).to_a
          merge merge_sort(left), merge_sort(right)
end
def merge left, right
          result = []
          while left.size > 0 && right.size > 0
              result << if left[0] <= right[0]
                  left.shift
              else
                  right.shift
              end
          end
          result.concat(left).concat(right)
end

Bạn tự hỏi rằng dùng thuật toán nào để có thể chia 1 mảng thành 2 mảng đã sắp xếp, vâng đó chính là thuật toán division phase mà bài viết sẽ giới thiệu dưới đây.

Division Phase

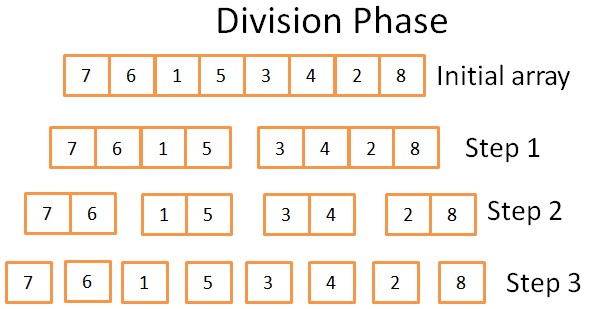Trong quá trình phân chia, mảng được phân chia thành mảng nhỏ nhất qua 3 bước. Thông thường số bước chính xác sử dụng trong phân chia mảng phụ thuộc vào số phần tử mảng ban đầu, và có giá trị là: log(N), N là số phần tử mảng ban đầu. Tiếp đến là xét đến giai đoạn sắp xếp(sorting phase)

Sorting phase

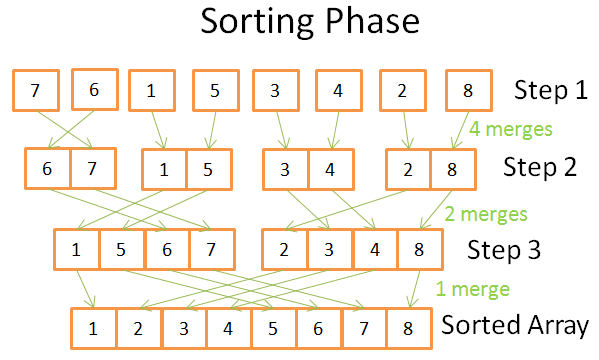Trong giai đoạn sorting, bạn sẽ bắt đầu với các mảng nhỏ nhất. Mỗi bước bạn áp dụng merges và tổng số operations sẽ là N=8

Trong bước thứ nhất bạn có 4 lần merge và mỗi lần merge là tốn 2 operations (chi phí cho mỗi lần merge là 2 operations) Bước 2 sử dụng 2 lần merges mỗi lần merge tốn 4 operations Bước thứ 3 sử dụng 1 lần merge và tốn 8 operations. Chúng ta có log(N) bước => tổng số operations phải chi trả là N * log(N) operations

Vì sao thuật toán merge sort lại mạnh mẽ(powerful) như vậy? Dưới đây là một số ưu điểm của nó:

Bạn có thể sửa đổi nó để giảm bộ nhớ trong một cách mà bạn không cần phải tạo ra các mảng mới, nhưng bạn trực tiếp sửa đổi các mảng đầu vào. (loại này được gọi là thuật toán in-place)

Bạn cũng có thể sửa đổi nó để sửa dụng không gian đĩa(disk space) và một lượng nhỏ bộ nhớ (memory) cùng một lúc....

Hoặc là bạn có thể sửa đổi nó để có thể chạy multiple processes/threads/servers....

Link Reference http://coding-geek.com/how-databases-work/#Back_to_basics

(Tobe continued).