Optimizer- Hiểu sâu về các thuật toán tối ưu ( GD,SGD,Adam,..)

Chào các bạn, hôm nay mình sẽ trình bày về optimizer. Vậy optimizer là gì ?, để trả lời câu hỏi đó thì các bạn phải trả lời được các câu hỏi sau đây :

• Optimizer là gì ?
• Ứng dụng của nó ra sao, tại sao phải dùng nó ?
• Các thuật toán tối ưu, ưu nhược điểm của mỗi thuật toán, thuật toán tối ưu này hơn thuật toán kia ở điểm nào ?

• Khi nào nên áp dụng optimizer này , khi nào nên áp dụng cái kia?

Nội dung bài hôm nay mình sẽ giải thích chi tiết về optimizers theo bố cục trả lời các câu hỏi trên. Bài viết này sẽ không nặng về phần tính toán, code, mình sẽ dùng ví dụ trực quan để minh họa cho dễ hiểu.

Optimizer là gì, tại sao phải dùng nó?

Trước khi đi sâu vào vấn đề thì chúng ta cần hiểu thế nào là thuật toán tối ưu (optimizers).Về cơ bản, thuật toán tối ưu là cơ sở để xây dựng mô hình neural network với mục đích "học " được các features ( hay pattern) của dữ liệu đầu vào, từ đó có thể tìm 1 cặp weights và bias phù hợp để tối ưu hóa model. Nhưng vấn đề là "học" như thế nào? Cụ thể là weights và bias được tìm như thế nào! Đâu phải chỉ cần random (weights, bias) 1 số lần hữu hạn và hy vọng ở 1 bước nào đó ta có thể tìm được lời giải. Rõ ràng là không khả thi và lãng phí tài nguyên! Chúng ta phải tìm 1 thuật toán để cải thiện weight và bias theo từng bước, và đó là lý do các thuật toán optimizer ra đời.

Các thuật toán tối ưu ?

1. Gradient Descent (GD)

Trong các bài toán tối ưu, chúng ta thường tìm giá trị nhỏ nhất của 1 hàm số nào đó, mà hàm số đạt giá trị nhỏ nhất khi đạo hàm bằng 0. Nhưng đâu phải lúc nào đạo hàm hàm số cũng được, đối với các hàm số nhiều biến thì đạo hàm rất phức tạp, thậm chí là bất khả thi. Nên thay vào đó người ta tìm điểm gần với điểm cực tiểu nhất và xem đó là nghiệm bài toán. Gradient Descent dịch ra tiếng Việt là giảm dần độ dốc, nên hướng tiếp cận ở đây là chọn 1 nghiệm ngẫu nhiên cứ sau mỗi vòng lặp (hay epoch) thì cho nó tiến dần đến điểm cần tìm.
Công thức : xnew = xold - learningrate.gradient(x)
Đặt câu hỏi tại sao có công thức đó ? Công thức trên được xây dựng để cập nhật lại nghiệm sau mỗi vòng lặp . Dấu '-' trừ ở đây ám chỉ ngược hướng đạo hàm. Đặt tiếp câu hỏi tại sao lại ngược hướng đạo hàm ?
Ví dụ như đối với hàm f(x)= 2x +5sin(x) như hình dưới thì f'(x) =2x + 5cos(x)
với x_old =-4 thì f'(-4) <0 => x_new > x_old nên nghiệm sẽ di chuyển về bên phải tiến gần tới điểm cực tiểu.
ngược lại với x_old =4 thì f'(4) >0 => x_new <x_old nên nghiệm sẽ di chuyển về bên trái tiến gần tới điểm cực tiểu.
a) Gradient cho hàm 1 biến :


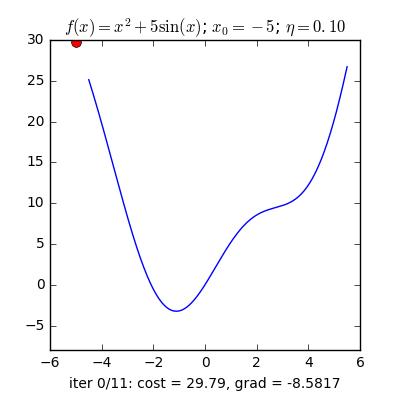
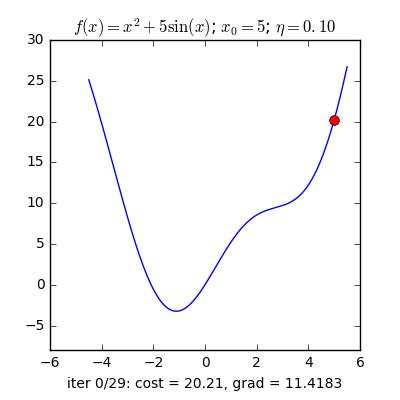
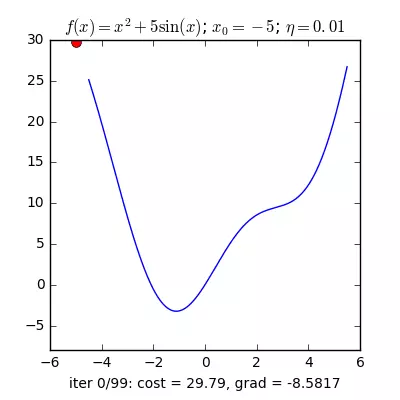
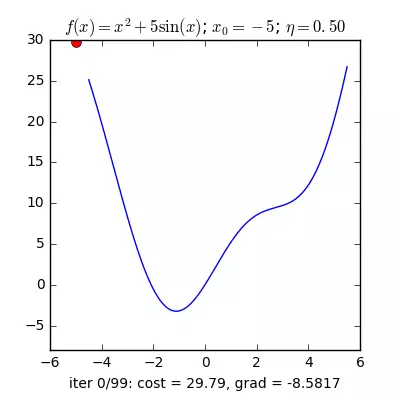
Nguồn : https://machinelearningcoban.com/2017/01/12/gradientdescent/
Qua các hình trên ta thấy Gradient descent phụ thuộc vào nhiều yếu tố : như nếu chọn điểm x ban đầu khác nhau sẽ ảnh hưởng đến quá trình hội tụ; hoặc tốc độ học (learning rate) quá lớn hoặc quá nhỏ cũng ảnh hưởng: nếu tốc độ học quá nhỏ thì tốc độ hội tụ rất chậm ảnh hưởng đến quá trình training, còn tốc độ học quá lớn thì tiến nhanh tới đích sau vài vòng lặp tuy nhiên thuật toán không hội tụ, quanh quẩn quanh đích vì bước nhảy quá lớn.
b) Gradient descent cho hàm nhiều biến :

Ưu điểm :
 Thuật toán gradient descent cơ bản, dễ hiểu. Thuật toán đã giải quyết được vấn đề tối ưu model neural network bằng cách cập nhật trọng số sau mỗi vòng lặp.
Nhược điểm :
 Vì đơn giản nên thuật toán Gradient Descent còn nhiều hạn chế như phụ thuộc vào nghiệm khởi tạo ban đầu và learning rate.
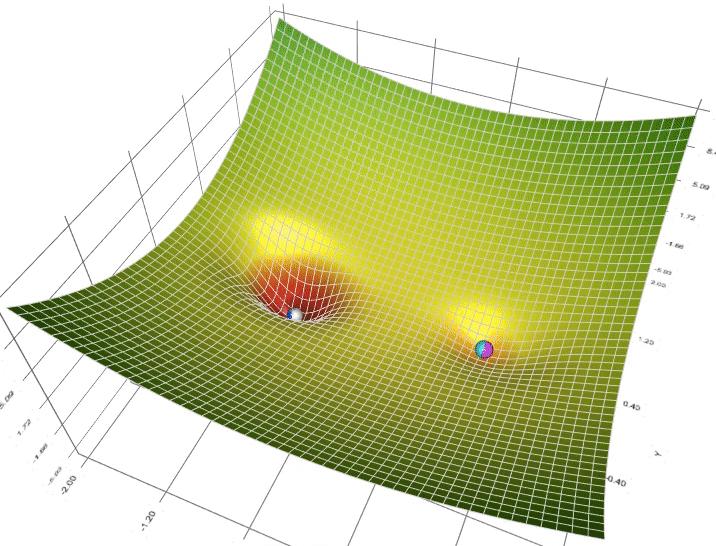
 Ví dụ 1 hàm số có 2 global minimum thì tùy thuộc vào 2 điểm khởi tạo ban đầu sẽ cho ra 2 nghiệm cuối cùng khác nhau.
 Tốc độ học quá lớn sẽ khiến cho thuật toán không hội tụ, quanh quẩn bên đích vì bước nhảy quá lớn; hoặc tốc độ học nhỏ ảnh hưởng đến tốc độ training

2. Stochastic Gradient Descent (SGD)

Stochastic là 1 biến thể của Gradient Descent . Thay vì sau mỗi epoch chúng ta sẽ cập nhật trọng số (Weight) 1 lần thì trong mỗi epoch có N điểm dữ liệu chúng ta sẽ cập nhật trọng số N lần. Nhìn vào 1 mặt , SGD sẽ làm giảm đi tốc độ của 1 epoch. Tuy nhiên nhìn theo 1 hướng khác,SGD sẽ hội tụ rất nhanh chỉ sau vài epoch. Công thức SGD cũng tương tự như GD nhưng thực hiện trên từng điểm dữ liệu.
Nhìn vào 2 hình trên, ta thấy SGD có đường đi khá là zig zắc , không mượt như GD. Dễ hiểu điều đó vì 1 điểm dữ liệu không thể đại diện cho toàn bộ dữ liệu. Đặt câu hỏi tại sao phải dùng SGD thay cho GD mặt dù đường đi của nó khá zig zắc ? Ở đây, GD có hạn chế đối với cơ sở dữ liệu lớn ( vài triệu dữ liệu ) thì việc tính toán đạo hàm trên toàn bộ dữ liệu qua mỗi vòng lặp trở nên cồng kềnh. Bên cạnh đó GD không phù hợp với online learning. Vậy online learning là gì? online learning là khi dữ liệu cập nhật liên tục (ví dụ như thêm người dùng đăng kí ) thì mỗi lần thêm dữ liệu ta phải tính lại đạo hàm trên toàn bộ dữ liệu => thời gian tính toán lâu, thuật toán không online nữa. Vì thế SGD ra đời để giải quyết vấn đề đó, vì mỗi lần thêm dữ liệu mới vào chỉ cần cập nhật trên 1 điểm dữ liệu đó thôi, phù hợp với online learning.
Một ví dụ minh hoạ : có 10.000 điểm dữ liệu thì chỉ sau 3 epoch ta đã có được nghiệm tốt, còn với GD ta phải dùng tới 90 epoch để đạt được kết quả đó.
Ưu điểm :
 Thuật toán giải quyết được đối với cơ sở dữ liệu lớn mà GD không làm được. Thuật toán tối ưu này hiên nay vẫn hay được sử dụng.
Nhược điểm :
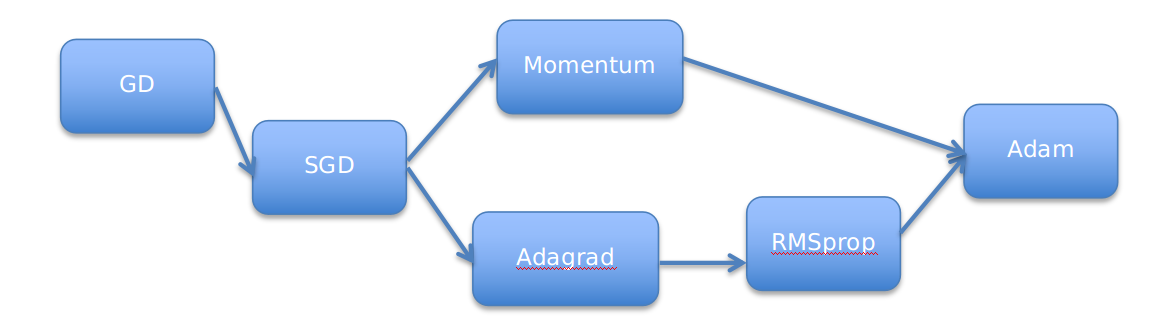
 Thuật toán vẫn chưa giải quyết được 2 nhược điểm lớn của gradient descent ( learning rate, điểm dữ liệu ban đầu ). Vì vậy ta phải kết hợp SGD với 1 số thuật toán khác như: Momentum, AdaGrad,..Các thuật toán này sẽ được trình bày ở phần sau.

3. Momentum

Để khắc phục các hạn chế trên của thuật toán Gradient Descent người ta dùng gradient descent with momentum. Vậy gradient with momentum là gì ?
Nguồn: https://machinelearningcoban.com/2017/01/16/gradientdescent2/
Để giải thích được Gradient with Momentum thì trước tiên ta nên nhìn dưới góc độ vật lí: Như hình b phía trên, nếu ta thả 2 viên bi tại 2 điểm khác nhau A và B thì viên bị A sẽ trượt xuống điểm C còn viên bi B sẽ trượt xuống điểm D, nhưng ta lại không mong muốn viên bi B sẽ dừng ở điểm D (local minimum) mà sẽ tiếp tục lăn tới điểm C (global minimum). Để thực hiện được điều đó ta phải cấp cho viên bi B 1 vận tốc ban đầu đủ lớn để nó có thể vượt qua điểm E tới điểm C. Dựa vào ý tưởng này người ta xây dựng nên thuật toán Momentum ( tức là theo đà tiến tới ).
Nhìn dưới góc độ toán học, ta có công thức Momentum:
xnew = xold -(gama.v + learningrate.gradient)
Trong đó :
xnew: tọa độ mới
xod : tọa độ cũ
gama: parameter , thường =0.9
learningrate : tốc độ học
gradient : đạo hàm của hàm f


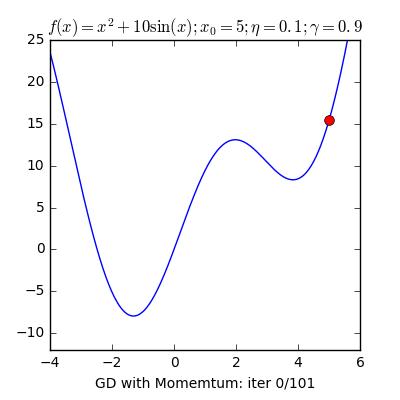
Nguồn : https://machinelearningcoban.com/2017/01/16/gradientdescent2/
Qua 2 ví dụ minh họa trên của hàm f(x) = x.2 + 10sin(x), ta thấy GD without momentum sẽ hội tụ sau 5 vòng lặp nhưng không phải là global minimum. Nhưng GD with momentum dù mất nhiều vòng lặp nhưng nghiệm tiến tới global minimum, qua hình ta thấy nó sẽ vượt tốc tiến tới điểm global minimum và dao động qua lại quanh điểm đó trước khai dừng lại.
Ưu điểm :
 Thuật toán tối ưu giải quyết được vấn đề: Gradient Descent không tiến được tới điểm global minimum mà chỉ dừng lại ở local minimum.
Nhược điểm :
 Tuy momentum giúp hòn bi vượt dốc tiến tới điểm đích, tuy nhiên khi tới gần đích, nó vẫn mất khá nhiều thời gian giao động qua lại trước khi dừng hẳn, điều này được giải thích vì viên bi có đà.

4. Adagrad

Không giống như các thuật toán trước đó thì learning rate hầu như giống nhau trong quá trình training (learning rate là hằng số), Adagrad coi learning rate là 1 tham số. Tức là Adagrad sẽ cho learning rate biến thiên sau mỗi thời điểm t.

Trong đó :
n : hằng số
gt : gradient tại thời điểm t
ϵ : hệ số tránh lỗi ( chia cho mẫu bằng 0)
G : là ma trận chéo mà mỗi phần tử trên đường chéo (i,i) là bình phương của đạo hàm vectơ tham số tại thời điểm t.

Ưu điểm :
 Một lơi ích dễ thấy của Adagrad là tránh việc điều chỉnh learning rate bằng tay, chỉ cần để tốc độ học default là 0.01 thì thuật toán sẽ tự động điều chỉnh.
Nhược điểm :
 Yếu điểm của Adagrad là tổng bình phương biến thiên sẽ lớn dần theo thời gian cho đến khi nó làm tốc độ học cực kì nhỏ, làm việc training trở nên đóng băng.

5. RMSprop

RMSprop giải quyết vấn đề tỷ lệ học giảm dần của Adagrad bằng cách chia tỷ lệ học cho trung bình của bình phương gradient.

Ưu điểm :
 Ưu điểm rõ nhất của RMSprop là giải quyết được vấn đề tốc độ học giảm dần của Adagrad ( vấn đề tốc độ học giảm dần theo thời gian sẽ khiến việc training chậm dần, có thể dẫn tới bị đóng băng )
Nhược điểm :
 Thuật toán RMSprop có thể cho kết quả nghiệm chỉ là local minimum chứ không đạt được global minimum như Momentum. Vì vậy người ta sẽ kết hợp cả 2 thuật toán Momentum với RMSprop cho ra 1 thuật toán tối ưu Adam. Chúng ta sẽ trình bày nó trong phần sau.

6. Adam

Như đã nói ở trên Adam là sự kết hợp của Momentum và RMSprop . Nếu giải thích theo hiện tượng vật lí thì Momentum giống như 1 quả cầu lao xuống dốc, còn Adam như 1 quả cầu rất nặng có ma sát, vì vậy nó dễ dàng vượt qua local minimum tới global minimum và khi tới global minimum nó không mất nhiều thời gian dao động qua lại quanh đích vì nó có ma sát nên dễ dừng lại hơn.

Công thức :

Tại sao lại có công thức đó ? Đó xem như 1 bài tập dành cho các bạn,........thật ra thì mình nhát chưa tìm hiểu.

Tổng quan

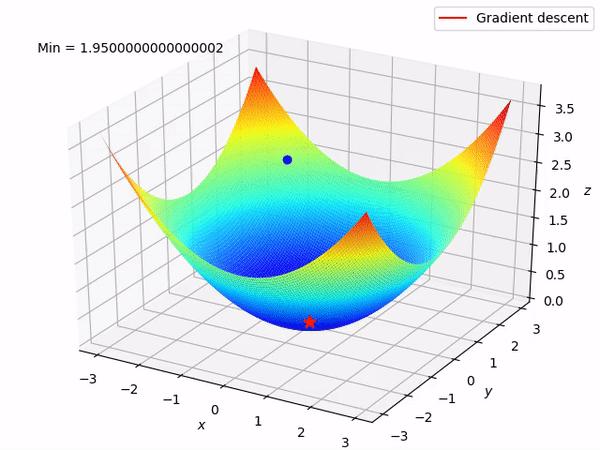
Còn có rất nhiều thuật toán tối ưu như Nesterov (NAG), Adadelta, Nadam,... nhưng mình sẽ không trình bày trong bài này, mình chỉ tập trung vào các optimizers hay được sử dụng. Hiện nay optimizers hay được sử dụng nhất là 'Adam'.

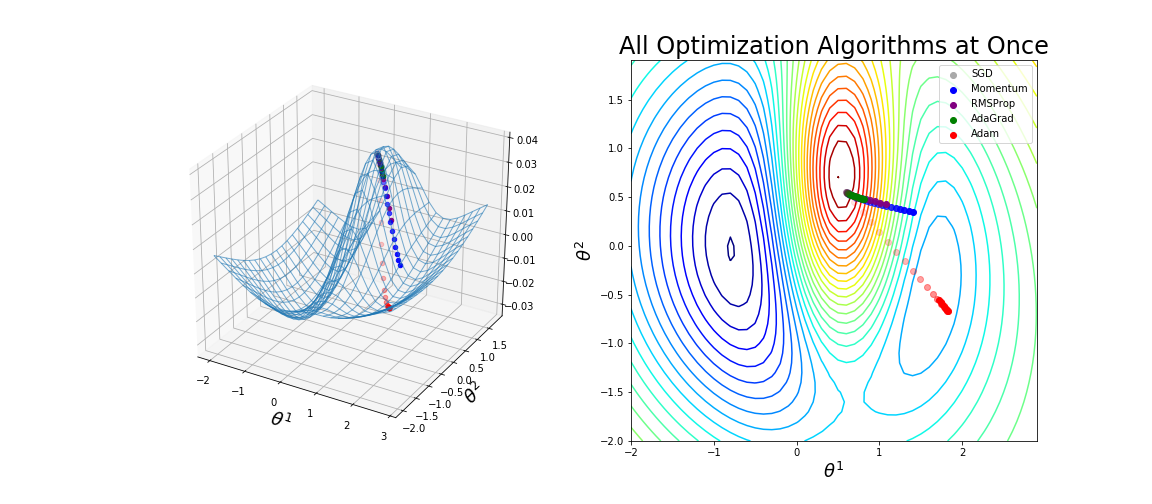
Qua hình trên ta thấy optimizer 'Adam' hoạt động khá tốt, tiến nhanh tới mức tối thiểu hơn các phương pháp khác. Qua bài viết này mình hy vọng các bạn có thể hiểu và làm quen với optimizer trong các bài toán Machine learning, đặc biệt là Deep learning. Còn nhiều biến thể của GD nhưng mình xin phép dừng bài viết tại đây.

| Hy vọng bài viết có ích đối với bạn |