OpenGL part 3.2: MODEL AND VIEW in OpenGL

**I. MODEL Ma trận **

Model được xác định bởi một tập hợp các đỉnh. Tọa độ X, Y, Z của các đỉnh được xác định tương đối so với trung tâm của đối tượng: đó là, nếu một đỉnh là (0,0,0), nó là trung tâm của các đối tượng.

Chúng ta có thể di chuyển mô hình này, có thể vì người chơi điều khiển nó với bàn phím và chuột. Thật dễ dàng, bạn chỉ học: translation * rotation * scale , và thực hiện. Bạn áp dụng ma trận này để tất cả các đỉnh của bạn tại mỗi khung (trong GLSL, không phải trong C ++!) Và di chuyển tất cả mọi thứ. Cái gì mà không di chuyển sẽ là trung tâm của thế giới.

Các đỉnh của bạn bây giờ đang ở trong một không gian. đây là ý nghĩa của mũi tên đen ở trong ảnh bên dưới. Chúng ta đi từ Model không gian (tất cả các đỉnh được định nghĩa thông qua vị trí trung tâm của mô hình) đến không giác khác (tất cả các đỉnh được định nghĩa trong không gian).

Chúng ta có thể tổng hợp này lại với sơ đồ sau:

II. View Ma trận

Nếu bạn muốn xem một ngọn núi từ một góc độ khác, bạn có thể di chuyển camera ... hoặc di chuyển các ngọn núi. Trong khi không phải thực tế trong cuộc sống thực tế, điều này là thực sự đơn giản và tiện dụng trong đồ họa máy tính. Vì vậy, ban đầu camera của bạn là nguồn gốc của không gian thế giới. Để di chuyển thế giới, bạn chỉ đơn giản là giới thiệu ma trận khác. Hãy nói rằng bạn muốn di chuyển máy ảnh của bạn trong 3 đơn vị ở bên phải (+ X). Điều này tương đương với việc di chuyển toàn bộ thế giới của bạn (bao gồm lưới) 3 đơn vị để LEFT! (-X). Trong khi bạn não tan chảy, chúng ta hãy làm điều đó:

// Use #include <glm/gtc/matrix_transform.hpp> and #include <glm/gtx/transform.hpp>
2 glm::mat4 ViewMatrix = glm::translate(-3.0f, 0.0f ,0.0f);

Một lần nữa, những hình ảnh dưới đây minh họa điều này: Chúng ta đã đi từ không gian thế giới (tất cả các đỉnh được xác định tương đối so với các trung tâm của thế giới, như chúng tôi đã làm như vậy trong phần trước) với không gian Camera (tất cả các đỉnh được xác định tương đối so với các máy ảnh).

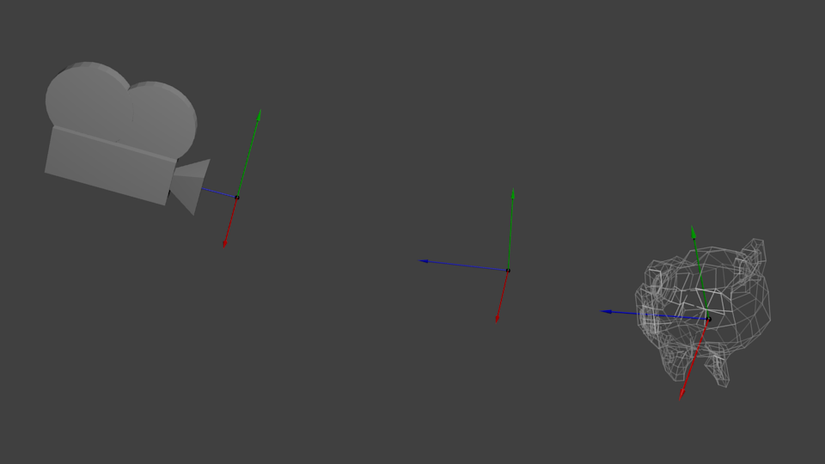
Để làm được điều này bạn cần phải sử dụng glm::lookAt

glm::mat4 CameraMatrix = glm::lookAt(
     cameraPosition, // the position of your camera, in world space
     cameraTarget,   // where you want to look at, in world space
     upVector        // probably glm::vec3(0,1,0), but (0,-1,0) would make you looking upside-down, which can be great too
);

Dưới đây là sơ đồ bắt buộc:

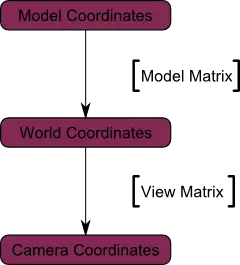
III. Các ma trận chiếu

Chúng ta đang ở không gian của Camera. Điều này có nghĩa rằng sau khi tất cả các đề tài biến đổi, một đỉnh đó xảy ra để có x == 0 và y == 0 nên được kết xuất ở trung tâm của màn hình. Nhưng chúng ta không thể chỉ sử dụng x và y tọa độ để xác định nơi một đối tượng cần được đặt trên màn hình: khoảng cách của nó với máy ảnh (z) đếm, quá! Đối với hai đỉnh có tọa độ x và y tương tự, đỉnh với z lớn nhất phối hợp sẽ được nhiều hơn về trung tâm của màn hình hơn khác.

một ma trận 4x4 có thể đại diện cho dự báo này:

// Generates a really hard-to-read matrix, but a normal, standard 4x4 matrix nonetheless
 glm::mat4 projectionMatrix = glm::perspective(
     FoV,         // The horizontal Field of View, in degrees : the amount of "zoom". Think "camera lens". Usually between 90° (extra wide) and 30° (quite zoomed in)
     4.0f / 3.0f, // Aspect Ratio. Depends on the size of your window. Notice that 4/3 == 800/600 == 1280/960, sounds familiar ?
     0.1f,        // Near clipping plane. Keep as big as possible, or you'll get precision issues.
     100.0f       // Far clipping plane. Keep as little as possible.
 );

Một lần cuối : Chúng ta đã đi từ không gian máy ảnh (tất cả các đỉnh được xác định tương đối so với các máy ảnh) để đồng nhất không gian (tất cả các đỉnh được định nghĩa trong một khối lập phương nhỏ. Tất cả mọi thứ bên trong khối lập phương là trên màn hình). Và sơ đồ cuối cùng:

Dưới đây là sơ đồ khác để bạn hiểu rõ hơn về những gì sẽ xảy ra với các công cụ chiếu này. Trước khi chiếu, chúng tôi đã có các đối tượng màu xanh của chúng ta, trong không gian ảnh, và các hình dạng màu đỏ đại diện cho hình cụt của camera: một phần của khung cảnh mà các máy ảnh là thực sự có thể nhìn thấy.

Nhân tất cả mọi thứ của Matrix chiếu có tác dụng sau đây:

Trong hình ảnh này, các hình cụt bây giờ là một khối hoàn hảo (giữa -1 và 1 trên tất cả các trục, đó là một chút khó khăn để xem nó), và tất cả các đối tượng màu xanh đã bị biến dạng trong cùng một cách. Như vậy, các đối tượng là gần camera (= gần mặt của khối lập phương mà chúng ta không thể nhìn thấy) là lớn, những người khác là nhỏ hơn. Có vẻ như cuộc sống thực!

Hãy xem những gì nó trông giống như từ "đằng sau" những hình cụt:

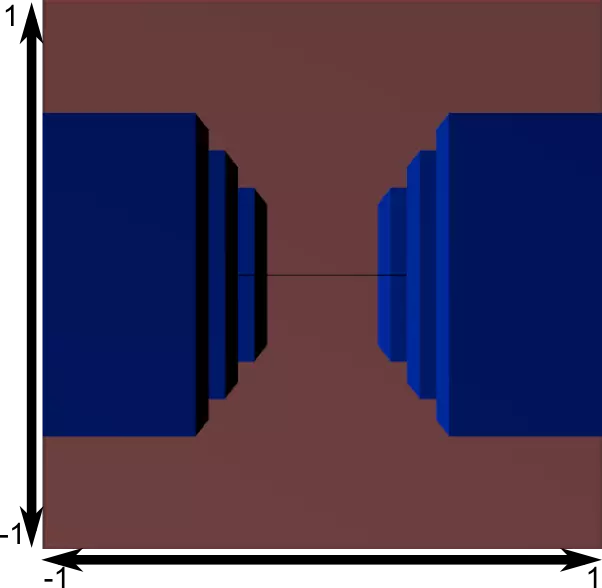
Ở đây bạn sẽ có được hình ảnh của bạn! Nó chỉ là một chút quá vuông, đến một biến đổi toán học được áp dụng (cái này là tự động, bạn không phải làm điều đó cho mình trong shader) để phù hợp này để kích thước cửa sổ thực tế:

**IV. Đỉnh điểm biến đổi: các ModelViewProjectionmatrix **

// C++ : compute the matrix
 glm::mat4 MVPmatrix = projection * view * model; // Remember : inverted !

 // GLSL : apply it
 transformed_vertex = MVP * in_vertex;

Để tất cả chúng cùng nhau

Bước đầu tiên: tạo ma trận MVP. Điều này phải được thực hiện đối với từng mô hình mà bạn vẽ.

// Projection matrix : 45° Field of View, 4:3 ratio, display range : 0.1 unit <-> 100 units
  glm::mat4 Projection = glm::perspective(glm::radians(45.0f), (float) width / (float)height, 0.1f, 100.0f);

  // Or, for an ortho camera :
  //glm::mat4 Projection = glm::ortho(-10.0f,10.0f,-10.0f,10.0f,0.0f,100.0f); // In world coordinates

 // Camera matrix
 glm::mat4 View = glm::lookAt(
                 glm::vec3(4,3,3), // Camera is at (4,3,3), in World Space
                glm::vec3(0,0,0), // and looks at the origin
                glm::vec3(0,1,0)  // Head is up (set to 0,-1,0 to look upside-down)
                );

 // Model matrix : an identity matrix (model will be at the origin)
 glm::mat4 Model = glm::mat4(1.0f);
 // Our ModelViewProjection : multiplication of our 3 matrices
 glm::mat4 mvp = Projection * View * Model; // Remember, matrix multiplication is the other way around

Bước thứ hai: đưa nó cho GLSL

// Get a handle for our "MVP" uniform
// Only during the initialisation
GLuint MatrixID = glGetUniformLocation(program_id, "MVP");

// Send our transformation to the currently bound shader, in the "MVP" uniform
// This is done in the main loop since each model will have a different MVP matrix (At least for the M part)
glUniformMatrix4fv(mvp_handle, 1, GL_FALSE, &mvp[0][0]);

Bước thứ ba: sử dụng nó trong GLSL để chuyển các đỉnh của chúng tôi

// Input vertex data, different for all executions of this shader.
layout(location = 0) in vec3 vertexPosition_modelspace;

// Values that stay constant for the whole mesh.
 uniform mat4 MVP;

 void main(){

   // Output position of the vertex, in clip space : MVP * position
    gl_Position =  MVP * vec4(vertexPosition_modelspace,1);
}

Dưới đây là hình tam giác giống như trong hướng dẫn 2, vẫn còn ở xứ (0,0,0), nhưng xem trong quan điểm từ điểm (4,3,3), đứng lên (0,1,0), với 45 ° góc nhìn.

Bài viết tham khảo

http://www.opengl-tutorial.org/beginners-tutorials/tutorial-3-matrices/