OpenGL part 3.1: Matrices

I. Tọa độ đồng nhất

Cho đến lúc đó, chúng ta coi một đỉnh 3D là một bộ ba vector (x, y, z). Hãy giới thiệu w. Bây giờ chúng ta sẽ có (x, y, z, w) bộ 4 vector.

Nếu w == 1, (x, y, z, 1) là một vị trí trong không gian.
Nếu w == 0, (x, y, z, 0) là một định hướng.

(Trong thực tế, hãy nhớ điều này.)

***Điều này làm nên khác biệt gì? ***

Vâng, đối với một vòng quay, nó không thay đổi bất cứ điều gì. Khi bạn xoay một điểm hoặc một hướng, bạn sẽ có được kết quả tương tự. Tuy nhiên, đối với một dịch chuyển (khi bạn di chuyển điểm theo một hướng nhất định), mọi thứ đã khác.

Tọa độ đồng nhất cho phép chúng tôi sử dụng một công thức toán học duy nhất để đối phó với hai trường hợp này.

II. Dịch chuyển ma trận

1. giới thiệu về ma trận

Đơn giản, ma trận là 1 dãy các số được xác đinh trước bởi các hàng và các cột. Ví dụ một ma trận 2x3 (M^2x3^) :

1   2   3
4   5   6
7   8   9

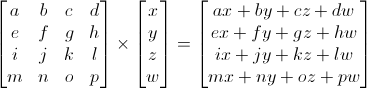
Trong đồ hoạ 3d chúng ta cần sử dụng ma trận 4x4. Chúng cho phép chúng ta chuyển đổi bộ 4 vector (x,y,z,w). Điều này được thực hiện bằng cách nhân đỉnh với ma trận:

Matrix x Vertex (in this order !!) = TransformedVertex

Code trên Cpp

glm::mat4 myMatrix;
glm::vec4 myVector;
glm::vec4 transformedVector = myMatrix * myVector;

Code trong GLSL

mat4 myMatrix;
vec4 myVector;
vec4 transformedVector = myMatrix * myVector;

2. Dịch chuyển ma trận

Đây là các ma trận chuyển đổi đơn giản nhất để hiểu. Ma trận dịch chuyển sẽ nhìn giống như thế này:

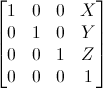
X,Y,Z là các giá trị mà bạn muốn cộng vào vị trí của bạn. Vì vậy nếu bạn muốn dịch chuyển vector (10,10,10,1) đi 10 đơn vị thì chúng ta có :

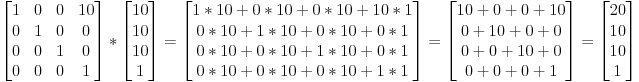
như vậy chúng ta có 1 vector đồng nhất (20,10,10,1). Nhớ rằng đó là 1 vị trí ko phải là một hướng. Vì vậy, biến đổi của chúng ta không thay đổi thực tế rằng là chúng ta đang đối phó với một vị trí.

Bây giờ hãy xem những gì sẽ xảy ra với một vector đại diện cho một hướng về phía trục -z: (0,0, -1,0)

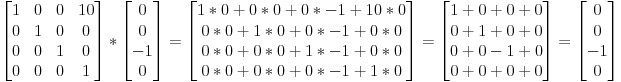
tức là vị trí của chúng ta ban đầu và có hướng đi là (0,0, -1,0),kết quả trả về di chuyển theo một hướng không có ý nghĩa.

Code trên Cpp

#include <glm/gtx/transform.hpp> //after<glm/glm.hpp>
glm::mat4 myMatrix = glm::translate(10.0f, 0.0f, 0.0f);
glm::vec4 myVector(10.0f, 10.0f, 10.0f, 0.0f);
glm::vec4 transformedVector = myMatrix * myVector;

Code trên GLSL

 vec4 transformedVector = myMatrix * myVector;

Nhận dạng ma trận Đây là một ma trận đặc biệt, nó giống như 1 hằng số,bởi vì ma trận này giống như khi nhân một số với 1 ra chính nó.

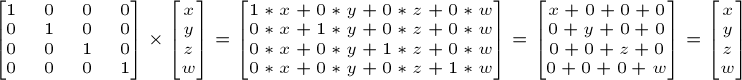
Ma trận này được định nghĩa trên C++:

 glm::mat4 myIdentityMatrix = glm::mat4(1.0f);

III.Scaling Ma trận

Ví dụ ta có 1 ma trận:

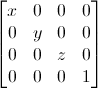
Nếu bạn muốn scalling một vector (vị trí hoặc định hướng không quan trọng) 2 lần:

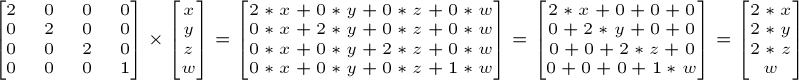
(lưu ý rằng các nhận dạng ma trận chỉ là một trường hợp đặc biệt của ma trận mở rộng quy mô, với (X, Y, Z) = (1,1,1). Nó cũng là một trường hợp đặc biệt của ma trận dịch chuyển với (X, Y, Z) = (0,0,0), bằng cách này)

sử dụng trên C:

glm::mat4 myScalingMatrix = glm::scale(2.0f, 2.0f ,2.0f);

IV.Xoay ma trận

Cái này khá phức tạp. Vì thế tôi sẽ bỏ qua các chi tiết ở đây, vì nó không quan trọng phải biết bố trí chính xác.

Code trên C:

glm::vec3 myRotationAxis( ??, ??, ??);
glm::rotate( angle_in_degrees, myRotationAxis );

IV.Cumulating transformations

Vì vậy, bây giờ chúng ta biết làm thế nào để xoay, dịch, và scale vectơ . Nó sẽ là tuyệt vời nếu kết hợp các phép biến đổi. Điều này được thực hiện bằng cách nhân ma trận với nhau, ví dụ:

TransformedVector = TranslationMatrix * RotationMatrix * ScaleMatrix * OriginalVector;

!!! Hãy coi chừng !!! Dòng này thực sự thực hiện nhân scaling đầu tiên, và sau đó là xoay, và cuối cùng là dịch chuyển. Đây là cách nhân ma trận hoạt động.

Như một vấn đề của thực tế, thứ tự trên là những gì bạn thường sẽ cần cho các nhân vật trò chơi và các đồ vật: đầu tiên là scaling nếu cần thiết; sau đó thiết lập hướng của nó, sau đó dịch chuyển nó.

glm::mat4 myModelMatrix = myTranslationMatrix * myRotationMatrix * myScaleMatrix;
glm::vec4 myTransformedVector = myModelMatrix * myOriginalVector;

Code trên GLSL

mat4 transform = mat2 * mat1;
2 vec4 out_vec = transform * in_vec;

Bài viết tham khảo

http://www.opengl-tutorial.org/beginners-tutorials/tutorial-3-matrices/