Nghịch lý Birthday paradox trong sử dụng “Chữ ký điện tử và hàm băm”

1. Một số khái niệm và nguyên lý cơ sở

• Có lẽ trong cuộc sống xã hội công nghệ thông tin ngày nay, chúng ta chắc hẳn cũng đã không ít lần nghe về “Chữ ký điện tử”. Vậy “chữ ký điện tử” hình thành ra sao và mục đích vì sao nó ra đời, sau đây chúng ta sẽ cùng đi tìm hiểu.

• Khái niệm chữ ký điện tử được hai nhà bác học Diffie và Hellman để xuất trong bài báo nổi tiếng của các ông khai sáng nguyên lý của hệ thống mật mã công khai (1976). Ý tưởng về mô phỏng chữ ký tay trên văn bản trong đời thường đã có từ rất lâu, nhưng nó chỉ thực sự có thể thực hiện được cùng với sự ra đời của hệ mật mã KCK (khóa công khai). Như đã biết, hệ thống mật mã đối xứng đã được sử dụng phổ biến trước đó không có tính đại diện duy nhất cho một cá nhân. Trong khi đó, một hệ mật mã khóa công khai (hay còn gọi là phi đối xứng) có thể được xem là được tạo lập để giúp bảo mật truyền tin trong liên lạc giữa một cá nhân và phần còn lại của xã hội. ->Nhờ có hệ mật mã KCK, khái niệm chữ ký điện tử mới được hiện thực hóa và giúp cho giao dịch kinh tế thương mại trong đời sống có thể đi vào số hóa hoàn toàn, qua đó thúc đẩy hoạt động dịch vụ trực tuyến phát triển như hiện nay.

• Đến đây, chúng ta có thể vẫn chưa hình dùng ra được chữ ký điện tử là như thế nào mà nó lại liên quan đến hệ mật mã KCK, và liệu không biết chữ ký điện tử hay chữ ký số có thể so sánh hoàn toàn với chữ ký tay được hay không? Thực ra không phải hoàn toàn tương tự.

  • Chữ ký tay là dấu vết của con người tác động lên cùng bản giấy đã chứa văn bản (in/viết sẵn). Do đó, phần chữ ký tay và phần văn bản là độc lập, không có quan hệ ràng buộc nào. Như chúng ta đã biết, do các quy luật của thế giới vật lý, người ta không thể đánh tráo chữ ký theo kiểu đơn giản là xé bỏ phần tờ giấy có chữ ký và ghép nối vào một phần tờ giấy mang chữ ký tạo mới khác.
  • Tuy nhiên, trong thế giới số hóa, các quy luật vật lý này không còn còn có mặt bà bất cứ lập trình viên nào cũng có thể tha hồ cắt ghép văn bản số hóa mà không bị phát hiện. Do đó, chữ ký điện tử không thể được tạo đơn giản như vậy được, nó cần phải được tạo lập một cách phức tạp hơn, chúng ta sẽ cùng tìm hiểu nó ở phần sau.

2. Chữ ký điện tử

2.1. Sơ đồ chữ ký cơ bản

• Về cơ bản, khi có một văn bản ở dạng nhị phân X, người ta sẽ phải tạo ra một chữ ký ở dạng nhị phân S sao cho S phụ thuộc hàm vào X, tức là S = f(X); hơn nữa quan hệ hàm này là bí mật (có tham số khóa bí mật) đối với người ngoài. -->Do đó, nếu có kẻ thù nào thử đánh tráo, tức giả mạo chữ ký, quan hệ hàm S = f(X) sẽ không còn đúng nữa và sẽ bị phát hiện.

• Tuy nhiên thì việc phát hiện xem một văn bản có chữ ký có là chuẩn hay bị giả mạo lại phải là một thao tác mà ai cũng làm được dễ dàng, không cần đến khóa bí mật kia (do người chủ chữ kí nắm giữ). Vì vậy, hệ thống chữ ký điện tử được xây dựng trên nguyên tắc sử dụng hai thuật toán riêng rẽ cho việc tạo lập chữ ký và kiểm định chữ ký, thông qua việc sử dụng hai cặp hàm toán học đối lập nhau, một cần khóa bí mật còn một thì không. -> Chính vì lí do này, mật mã khóa công khai đã được khai thác để giúp thực hiện điểm chốt của cơ chế đặc biệt này.

• Ở đây, ta giả sử A là người cần ký vào văn bản được gửi đến B, sau đó B sẽ kiểm định tính hợp lệ của chữ ký kèm văn bản gửi đển. Quá trình đó diễn ra như sau:

  • Giả định A đã thiết lập sẵn một hệ mật mã KCK với thành phần khóa bí mật z_A và công khai Z_A, tức là có hàm sinh mã D_z_A và hàm giải mã E_Z_A. Khi đó, A có thể tạo ra chữ ký điện tử bằng hàm D_z_A và bất kì người nào khác sẽ kiểm tra bằng hàm E_Z_A.
  • Cụ thể là, với văn bản nhị phân X, A sẽ tạo được một chữ ký S = D_z_A(X); văn bản có chữ ký sẽ là: Y = X||S. Khi văn bản này đến tay B, B sẽ kiểm tra tính hợp lệ bằng việc tính X' = E_Z_A(S), sau đó đối chiếu X = X’? Với lưu ý là trong đó, B sẽ cần tìm kiếm được khóa công khai của A, tức Z_A bằng một cách nào đó.

• Để hiểu rõ hơn về quá trình tạo chữ ký và kiểm định chữ ký điện tử, ta cùng xét ví dụ sau:

• Ví dụ: - Giả sử A có một văn bản X = 0101 0011 0111 và A cũng đã thiết lập một hệ mật mã RSA với cặp khóa (e_A, d_A) theo modulo n. A có thể thiết lập một văn bản có chữ ký Y = X||S như sau: X = 010 100 110 111 --> S = X^(d_A) mod n = 100 101 011 001 --> Y = X‖S = 010100110111100101011001 - Khi B nhận được văn bản Y, B có thể kiểm định chữ ký thông qua quá trình sau:

  • Bước 1: Tách Y nhận được thành 2 thành phần X_1 = 010100110111 và S_1 = 100101011001
  • Bước 2: Tính X_2 = (S_1)^(e_A ) mod n = 010100110111 rồi so sánh xem X_1 ⊕ X_2 = 0? Nếu đùng thì chữ ký hợp lệ.
  • Qua quá trình trên, nhận thấy trong Y phần chữ ký (S) và văn bản gốc (X) là có hai xâu nhị phân có cùng chiều dài.

2.2. Ứng dụng của chữ ký điện tử

• Tính không chối cãi được (non-repudiation) - Qua ví dụ ở phần trên, nếu B đã nhận được văn bản có chữ ký X‖S và dùng khóa công khai của A để kiểm định thành công, thì văn bản đó trở thành bằng chứng, ngay cả khi A có muốn chối cãi đã tạo ra và ký nó cũng không được. Bởi vì chỉ duy nhất A mới sở hữu khóa bí mật d_A để tạo ra được chữ ký hợp lệ mà thôi. --> Đây chính là tính không thể chối cãi được (non – repudiation) của chữ ký điện tử. Ngay cả khi A có khiếu nại bị oan vỡi lý do chữ ký tạo ra bở một kẻ ăn cắp được khóa bí mật của A, thì điều này cũng không thể chứng minh được (trong dân gian hay gọi trường hợp tương tự như này là “tình ngay lý gian”).
• Công chứng
  • Để đảm bảo phòng tránh được tình trạng chữ ký giả mạo do kẻ gian ăn cắp được khóa bí mật của người bị hại, người ta đã giới thiệu thêm hệ thống công chứng – public notary.
  • Ý tưởng thực hiện như sau:
    • Sẽ có thêm một bên thứ ba tham gia, vô tư và thẩm quyền hợp pháp, được gọi là công chứng viên (public notary), sẽ được thuê để ký xác nhận thêm vào sau chữ ký của A đối với những văn bản quan trọng mà A ký. Văn bản đày đủ chữ ký sẽ có dạng Y = X ‖ S_A ‖ S_N, trong đó, S_N là chữ ký của công chứng viên lên văn bản X ‖ S_A.
• Bằng chứng biên nhận
  • Trong truyền tin liên lạc, chữ ký điện tử có thể sử dụng để đảm bảo tính chính xác của tài liệu (bằng chữ ký của bên gửi A) và bên nhận B có thể gửi lại chữ ký của mình vào tài liệu đã nhận như là bằng chứng để A biết B đã thực sự nhận được tài liệu đó. Nếu thủ tục này được thực hiện, sau này A có thể chúng minh được là mình đã gửi tài liệu cho B, ngay cả khi lúc đó B muốn chối cãi cũng không được.
  • A -> N: Y = E_Z_B(X ‖ D_z_A(X))
    • Trong đó D_z_A(X) chính là chữ ký điện từ X lên văn bản X
    • B tính D_z_B(Y), thu được X và S = D_z_A(X), sau đó kiểm tra xem X = E_z_A(S)?
    • B -> A: Y’ = E_Z_A(D_z_B(X))
    • Tại A, nhận được S_B (X) = D_z_A(Y’), đó chính là chữ ký của B trên X, bằng chứng xác nhận B đã nhận được tài liệu chính xác.

2.3. Nhược điểm của hệ chữ ký cơ sở

• Chữ ký quá dài, dài đúng bằng tài liệu: Với văn bản dài, ta cần dùng việc chia khối rồi ký lên nhiều khối; cụ thể là X = X_1 || X_2 || X_3 || …||X_(t-1) || X_t
• Rõ ràng số lượng khối trên văn bản đã ký nhiều gấp đôi ban đầu.
• Không những dài, việc thực hiện nhiều lần thuật toán KCK (ký lên từng khối) sẽ làm thủ tục ký có thể diễn ra rất lâu, thời gian tỷ lệ với độ dài văn bản. Điều này là không chấp nhận được với các giao dịch trực tuyến.
• Kẻ tấn công có thể dễ dàng phá được hệ thống chữ ký này bằng kiểu tấn công lắp ghép khối (thay đổi thứ tự, thêm hay bớt các khối...). Cách làm chi tiết tương tự như trong tấn công vào chế độ mật mã bảng tra điện tử ECB. --> Do đó, hệ thống chữ ký điện tử đơn giản kiểu này đã không được sử dụng. Giải pháp đầy đủ là có thêm sự hỗ trợ của hàm băm, tức là “băm” tài liệu trước khi ký và gửi đi.

3. Hàm băm và ứng dụng chữ ký điện tử

3.1. Nguyên lý của hàm băm

• Hoạt động của hàm băm được mô tả như sau: Một hàm băm H sẽ lấy ở đầu vào một thông tin X có kích thước bất kỳ và sinh kết quả ra là một chuỗi h_X = h(X) có độ dài cố định, thường nhỏ hơn rất nhiều so với kích thước của X. Chuỗi này thường được gọi là cốt yếu, hay cốt (digest) của thông tin X.
• Để hiểu rõ hơn, ta xét ví dụ như sau:
• Thông tin X có thể là một tệp độ dài hàng trăm Kb trong khi cốt của nó chỉ là một khối có độ dài 123 bit. Tất nhiên, điều đó dẫn đến khả năng có thể có hai thông tin X ≠ X’ mà cho cùng một cột cốt giống nhau với một hàm băm, tức là H(X) = H(X’). Trường hợp này gọi là đụng độ (collision).
• Ví dụ giả sử H(X) là hàm lấy số dư phép chia 10, rõ ràng ta có:
  • H(56) = H(156) = H(96)...
• Tuy nhiên với hàm băm thiết kế tốt, đụng độ là gần như không thể xảy ra được trên thực tế. Nói cách khác, nếu cố đi tìm, khối lượng tính toán phải thực hiện là rất lớn, không khả thi với công cụ tính toán hiện thời. Việc xây dựng, thiết kế hàm băm được đựa trên bài toán balls into bins, tuy nhiên trong bài viết này mình sẽ không đề cập đến, trong các bài viết tiếp theo mình sẽ nói cụ thể hơn về các bài toán mô hình thuật toán và internet phổ biển về lý thuyết, phương thức hoạt động cũng như ứng dụng của chúng trong thực tế.

3.2. Ứng dụng của hàm băm trong sinh chữ ký điện tử

• Hàm băm có ứng dụng chủ chốt trong các hệ chữ ký điện tử được sử dụng hiện nay. Thay vì ký (hay thực hiện thuật toán D_z_A) lên văn bản X, A cần thực hiện ký lên h_X; như vậy văn bản đã ký sẽ có dạng
  • X || D_z_A(H(X)).
• Để đảm bảo an toàn cao, chống được tấn công giả mạo chữ ký, chúng ta cần sử dụng các hàm băm mật mã (cryptographic hash function) với các thuộc tính như sau:
  • Lấy đầu vào là một xâu với độ dài bất kỳ và sinh ra một xâu với độ dài cố định.
  • Có tính một chiều (one – way): Biết X, có thể dễ dàng tính được giá trị băm h_X, nhưng không thể tính ngược được X khi chỉ biết h_X, bất khả thi về mặt tính toán với các công cụ tính toán hiện nay.
  • Có tính đụng độ cao (collision free), tức là thực tế không thể tìm được hai thông tin X ≠ X’ sao cho H(X) = H(X’). Tất nhiên, đây là bất khả thi về mặt tính toán.

3.3. Đụng độ khi sinh chữ ký điện tử sử dụng hàm băm

• Như ở trên đã nói, với không gian giá trị băm nhỏ hơn không gian tin về mặt kích thước thì chắc chắn sẽ tồn tại đụng độ (collision), nghĩa là có hai bản rõ X ≠ X’ mà giá trị băm của chúng giống nhau, nghĩa là h_X= h_X'. Điều này có thể thấy rõ ràng qua nguyên lý Direchlet – "Nếu có n + 1 con thỏ được thả vào b cái chuồng thì phải tồn tại ít nhất một cái chuồng mà trong đó có ít nhất là 2 con thỏ".

• Ví dụ: Giả sử không gian tin là Z_p* = {1, 2,..., p – 1} và không gian giá trị băm là Z_q* = {1, 2,..., q – 1} với q là số nguyên tố và p > q. Chọn một số g ∈ Z_p*

  • Để “băm” một tin X chúng ta sử dụng hàm băm: h(x) = g^x (mod q)
  • Ví dụ với p = 15, q = 11, g = 3, ta có:
    • 32 = 9 (mod 11) (1)
    • 33 = 5 (mod 11)
    • 34 = 4 (mod 11)
    • 35 = 1 (mod 11)
    • 36 = 3 (mod 11)
    • 37 = 9 (mod 11) (2) --> Xảy ra đụng độ - collision tại (1) và (2)
  • Nếu ta sử dụng chuỗi 4 bit để biểu diễn các tin thì H(0010) = H(0111)

• Trong thực tế, người ta thường chọn không gian băm cỡ khoảng 64 bit, 128 bit,... Trong khi đó các văn bản thực tế lớn hơn nhiều, cỡ Kb trở lên, cho nên việc tồn tại đụng độ là chắc chắn. Tuy nhiên, nếu sử dụng hàm băm mật mã có không gian băm lớn được chế tạo tốt (an toàn) thì việc tìm ra đụng độ đòi hỏi khối lượng tính toán lớn đến mức phi thực tế (infesible computation).

• Việc chế tạo các hàm băm phi đụng độ là rất khó. Nhiều hàm băm được phát minh bởi các nhóm có tên tuổi trên thế giới sau một thời gian xuất hiện đã bị những người khác chỉ ra những đụng độ tồn tại và không được công nhận là an toàn nữa.

4. Birthday attack

4.1. Vấn đề đặt ra

• Như ta đã biết, có một dạng tấn công mạo hiểm đối với các hệ chữ ký điện tử có dùng hàm băm là kẻ tấn công tìm cách tạo ra được những văn bản X và X’ có nội dung khác nhau (một có lợi một có hại cho bên A, người sẽ bị lừa để ký vào) mà có giá trị băm giống nhau. Kẻ thù có thể tìm cách tạo ra một số lượng rất lớn các văn bản có nội dung không thay đổi nhưng khác nhau về biểu diễn nhị phân (đơn giản là việc thêm bớt các dấu trắng, dùng nhiều từ đồng nghĩa thay thế nhau...), sau đó sử dụng một chương trình máy tính để tính giá trị băm của các văn bản đó và đem so sánh với nhau để hi vọng tìm ra một cặp văn bản có đụng độ.
• Như đã nêu ở trên thì để chắc chắn có thể tìm ra được một đụng độ như vậy, số văn bản cần được tính giá trị băm phải lớn hơn kích thước không gian băm. Chẳng hạn như nếu hàm băm có không gian băm 64 bit thì số lượng văn bản cần được đem ra nạp vào chương trình thử này phải là ít nhất 2^64, một con số quá lớn đến mức hàng thế kỉ nữa cũng không thực hiện xong.
• Tuy nhiên nếu như kẻ tấn công đem thử với một số lượng văn bản ít hơn nhiều, trong phạm vi có thể tính toán được, thì xác suất để tìm được đụng độ có đáng kể hay không? Có thể nhiều người sẽ nghĩ là xác suất này rất nhỏ, ví việc tìm được đụng độ là rất khó. Tuy nhiên, câu trả lời lại vô cùng bất ngờ, xác suất này có thể vẫn khá lớn, tức là có nhiều hy vọng tìm được đụng độ dù tập văn bản đem thử không lớn lắm. Bản chất của hiện tượng này có thể được minh họa rõ qua một phát biểu, thường được gọi là Nghịch lý Ngày sinh nhật (Birthday Paradox), chúng ta sẽ cùng đi tìm hiểu nghịch lý này ở phần tiếp theo.

4.2. Birthday Paradox

• Nghịch lý Ngày sinh nhật (Birthday Paradox) được phát biểu như sau: “Trong một nhóm có 23 người bất kỳ, xác suất để có hai người có cùng một ngày sinh nhật là không ít hơn ½”.

• Một cách tổng quát, giả sử một hàm băm có m giá trị băm khác nhau (tức là kích thước của không gian output của hàm băm là m). Nếu chúng ta có k giá trị băm từ k thông tin được chọn ngẫu nhiên khác nhau, thì xác suất để có ít nhất một đụng độ là:

• 

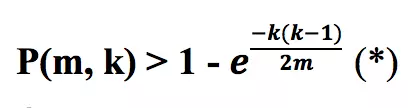
  • Với e là hằng số Ơ-le: e ≈ 2.7
  • Ước lượng xác suất này phục thuộc vào kích thước của không gian băm (m) và số lượng văn bản thông tin được thử chứ không phụ thuộc vào hàm băm đều sử dụng. Tức là kích thước của không gian băm xác lập một chặn dưới (lower bound) cho xác suất trên.

• Ta xét ví dụ sau: Trong nghịch lý ngày sinh nhật nói trên, thì ta có thể thấy k = 23, m = 365, do đó xác suất tồn tại hai người có cùng ngày sinh nhật là:

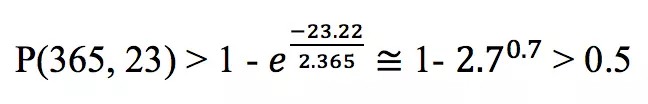
  • Công thức nói trên cho phép xác định số lượng thông tin (k) cần thiết để có thể tìm được một đụng độ giá trị băm với xác suất đủ lớn, khi hàm băm xác định trước. Ngược lại, nó cũng cho phép tính được kích thước tối thiểu của đầu ra hàm băm để có thể chống lại được hiệu ứng Birthday attack một cách có hiệu quả.

Ví dụ 4.4:

• Giả sử kẻ thù có khả năng tính toán trên tập giá trị băm đến 10^20. Ta cần xác định không gian băm để xác suất kẻ thù có thể tìm ra được một đụng độ là nhỏ hơn 10^(-3).

  • Áp dụng ước lượng xác suất trên, ta thấy: .
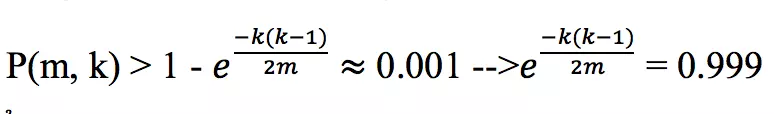  • Từ đó, ta có thể ước lượng m hợp lý:
  • 
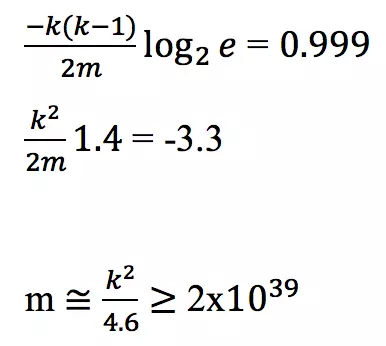
  • Như vậy, không gian băm cần đảm bảo lớn hơn 2x(10^39), tức là kích thước giá trị băm sẽ không nhỏ hơn
  • Tìm đụng độ trên không gian văn bản có kích cỡ 2^32 là một điều có thể làm được ngay cả với các máy tính PC bình thường. Việc nghiên cứu Birthday Paradox cho ta thấy lượng văn bản cần đưa ra thử có thể là rất nhỏ sao với không gian băm (2^32 so với 2^64) mà xác suất tìm được đụng độ là khá cao (≥ 50%). Điều này cho thấy một mối hiểm họa cho các hệ thống dùng hàm băm có không gian output nhỏ.
  • Phép tấn công này được gọi là “Tấn công ngày sinh nhật” (Birthday attack).

• Qua các phần đã trình bày ở trên, chúng ta đã cùng tìm hiểu về chữ ký điện tử, lý do nó xuất hiện cũng như nguyên lý tạo chữ ký điện tử cơ sở, chữ ký điện tử dựa trên hàm băm của văn bản được ký cũng như “Tấn công ngày sinh nhật” với các chữ ký điện tử sử dụng hàm băm. Trong bài này có một số kiến thức mọi người cần đọc thêm để hiểu rõ hơn về các phần mình đã trình bày, bao gồm: Hệ mật mã đối xứng, hệ mật mã công khai, nguyên lý Birthday Paradox. Về nguyên lý Birthday Paradox, mình sẽ trình bày tiếp về cách chứng minh xác suất xảy ra của nó và việc xảy ra trong một số mô hình thuật toán internet phổ biến khác.